6. Интегрирование рациональных функций Интегрирование рациональной функции

,   ,  являющейся правильной дробью (т.е.   при), производится путём представления этой функции в виде суммы простых дробей. Если же дробь является неправильной (), то её представляют в виде суммы многочлена и правильной дроби, затем интегрируют эти слагаемые.

Пример 7. Найти интегралы: а) ; б).

Решение. а)

Иногда вычисляют иначе

б)

.

Пример 8. Найти интегралы: а) ;

б) ;   в).

Решение. а) Найдём разложение подынтегральной функции на сумму простых дробей:

;

;

;

Таким образом,

.

б) .

Разложим подынтегральную функцию на сумму простых дробей:

;

.          (1)

x = 0; –8A = +5.  A = –5/8,

x = 2; 24B = 3.  B = 1/8.

Из равенства (1) следует (приравниваются коэффициенты при x³ и x):

Отсюда, зная уже A = –5/8 , B = 1/8, находим C = 1/2, D = 7/4. Таким образом,

.

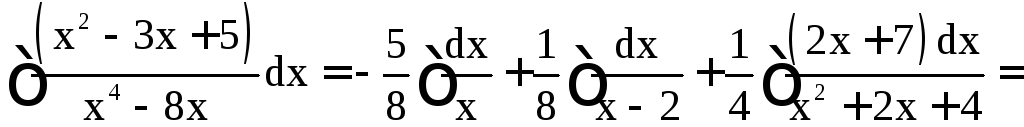
в) Рациональная функция 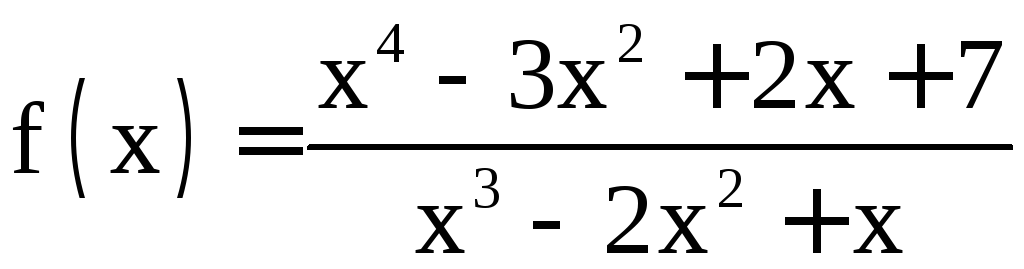представляет собой неправильную дробь. Выделим целую часть делением уголком

x⁴ – 3x² + 2x +7 x³ – 2x² + x

x⁴ – 2x³ + x² x + 2

2x³ – 4x² + 2x + 7

2x³ – 4x²+2x

7

Таким образом,

.

Разложим правильную дробь на сумму простых дробей:

;

; (2)

x = 0; A = 7;

x = 1; B₂ = 7.

Сравнивая старшие коэффициенты в обеих частях равенства (2), находим A + B₁ = 0, B₁ = –A = –7 . Таким образом,

.

7. Интегрирование тригонометрических функций

При интегрировании функций вида лучше придерживаться следующего правила: 1) еслиn нечётное положительное число, то делаем замену переменной еслиm – нечётное положительное число, то делаем замену переменной и это приведёт к интегралу от степенной функции; 2) еслиn и m – чётные числа, то с помощью формул ,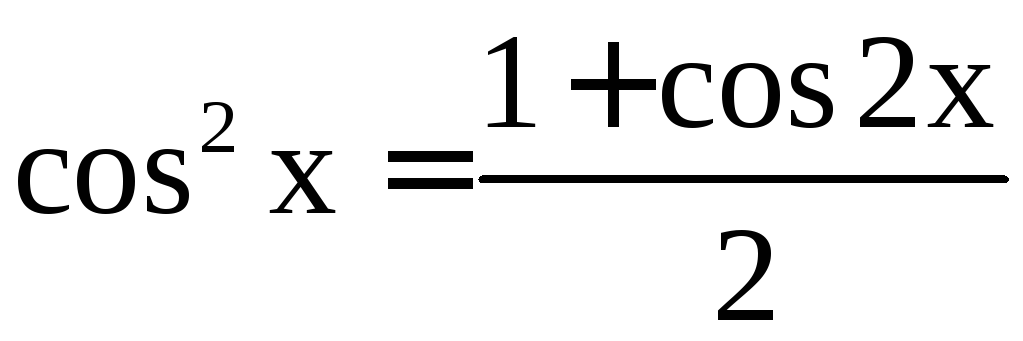достигается упрощение вида подынтегральной функции.

Пример 9. Найти а) ; б).

Решение. ==;

б)

.

Интегрирование функций вида ,,производится с помощью формул произведений синусов и косинусов.

Пример 10. Найти .

Решение.

.

Интегрирование функций вида R(sinx, cosx), где R – рациональная функция двух переменных, производится с помощью замены . При этом,,,

.

Пример 11. Найти .

Решение. = =

.

8. Интегрирование некоторых иррациональных функций

Интегралы вида , гдеR – рациональная функция двух переменных, выделением полного квадрата приводятся к одному из следующих видов:

1); 2); 3).

Эти последние интегралы находятся с помощью подстановок:

1) t = a tgu или t = a shu ; 2) t = a/cosu или t = a chu ;

3) t = a sinu или t = a thu .

Пример 12. Найти .

Решение. = =

=

.

Пример 13. Найти .

Решение. =

=.

Пример 14. Вычислить .

Решение.

.

9. Определённый интеграл

Пусть функция f(x) определена на отрезке [a, b]. Разобьём этот отрезок точками наn частей [x_k-1; x_k], ; обозначим. Число,, назовём диаметром разбиения. Возьмём в каждом частичном отрезке [x_k-1; x_k] по точке t_k и образуем следующую сумму, называемую интегральной:

.

Если существует конечный предел интегральных сумм при , предел, не зависящий ни от способа разбиения отрезка [a; b], ни от выбора точек, то функция f(x) называется интегрируемой на [a; b], а сам предел – определённым интегралом от f(x) на [a; b] и обозначается.

По определению положим

=,.

Если f(x) непрерывна на [a; b], то она интегрируема на [a; b].

К интегрируемым функциям относятся также:

1) монотонно возрастающие (убывающие) и ограниченные на [a; b];

2) ограниченные и имеющие лишь конечное число точек разрыва на

[a; b] .

Определённый интеграл обладает следующими свойствами:

1. если f(x) интегрируема на большем из отрезков [a; b], [b; c], [a; c], то f(x) интегрируема и на двух других и при этом

= +;

2. если f(x) и g(x) интегрируемы на [a; b], то также интегрируема на [a; b] и при этом

= +;

3. если интегрируема на [a; b], то f(x) также интегрируема на

[a; b] и при этом ;

4. если f(x) и g(x) интегрируемы на [a; b] и f(x)  g(x) , то

;

5. если f(x) интегрируема на [a; b] и m  f(x)  M , то.

Теорема 2. Если F(x) – первообразная функции f(x), непрерывной на [a; b], то

(формула Ньютона–Лейбница).

Разность часто обозначают.

Пример 15. Найти .

Решение.

.

Теорема 3. Пусть f(x) непрерывна на [a; b] и функция удовлетворяет следующим условиям: 1)дифференцируема на; 2),; 3) значенияне выходят за пределы

[a; b], когда t пробегает значения из . Тогда

.

Пример 16. Вычислить .

Решение. 1) Функция 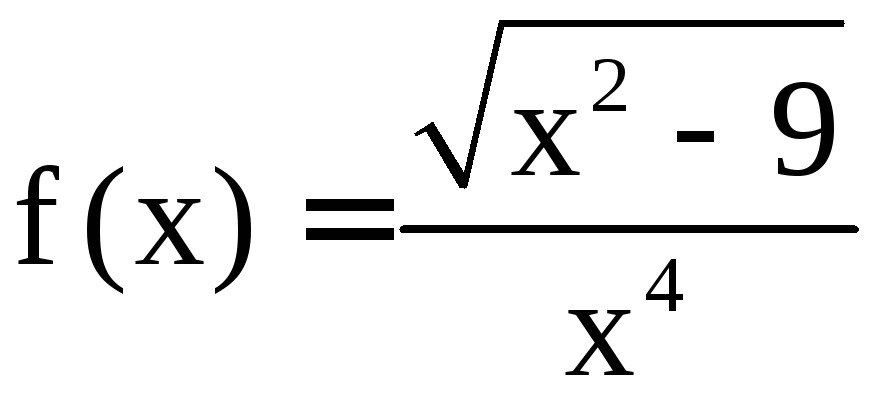непрерывна на интервале [3,6].

2) Применим подстановку и изменим пределы интегрирования. Если, тои. Если, тои.

Отметим, что функция удовлетворяет на отрезкеусловиям теоремы о замене переменной в определенном интеграле, так как она непрерывно дифференцируема, монотонна ии.

3) ,,

так как при.

.

Пример 17. Вычислить: а) ; б).

Решение. а) Сделаем замену переменного: . Тогда;; меняются пределы интегрирования:,.

Имеем

.

б)

.

Теорема 4. Если u(x), v(x) дифференцируемы на [a; b], то

.

Пример 18. Вычислить .

Решение.

.