
- •VII. Интегральное исчисление функции одного переменного
- •1. Неопределённый интеграл
- •2. Таблица основных неопределённых интегралов
- •3. Основные свойства неопределённого интеграла
- •4. Интегрирование методом замены переменного
- •5. Интегрирование по частям
- •6. Интегрирование рациональных функций Интегрирование рациональной функции
- •7. Интегрирование тригонометрических функций
- •8. Интегрирование некоторых иррациональных функций
- •9. Определённый интеграл
- •10. Несобственные интегралы
- •11. Вычисление площадей плоских фигур
- •12. Вычисление длины дуги
- •13. Вычисление объёмов тел
- •14. Приближённое вычисление определённых интегралов
- •Задание 7.1
- •Задание 7.2
- •Задание 7.3
- •Задание 7.4
- •Задание 7.5
- •Задание 7.6
- •Задание 7.7
- •Задание 7.8
- •Задание 7.13
- •Задание 7.14
- •Задание 7.15
- •Задание 7.16
- •Задание 7.17
- •Задание 7.18
- •Задание 7.19
- •Задание 7.20
- •Задание 7.21
- •Задание 7.22
10. Несобственные интегралы
1. Несобственный
интеграл I рода. Пусть
функция f(x) определена на
![]() и интегрируема на отрезке [a; b] для любого
и интегрируема на отрезке [a; b] для любого![]() .
Несобственный интеграл первого рода
определяется равенством
.
Несобственный интеграл первого рода
определяется равенством
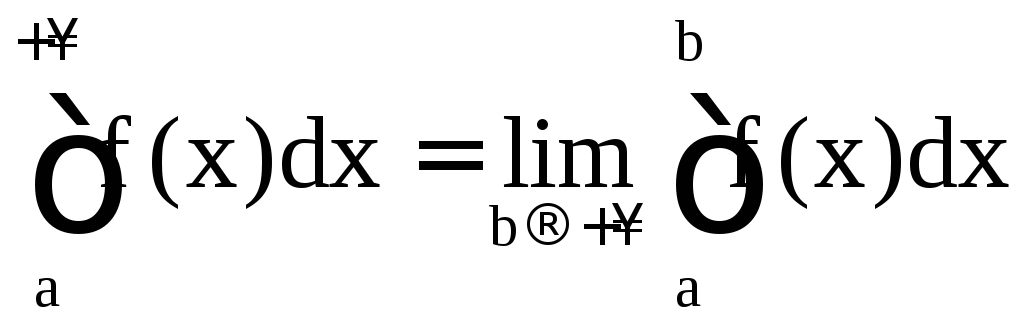 .
.
Если существует конечный предел в этом равенстве, то интеграл называется сходящимся, в противном случае – расходящимся. Аналогично определяются несобственные интегралы
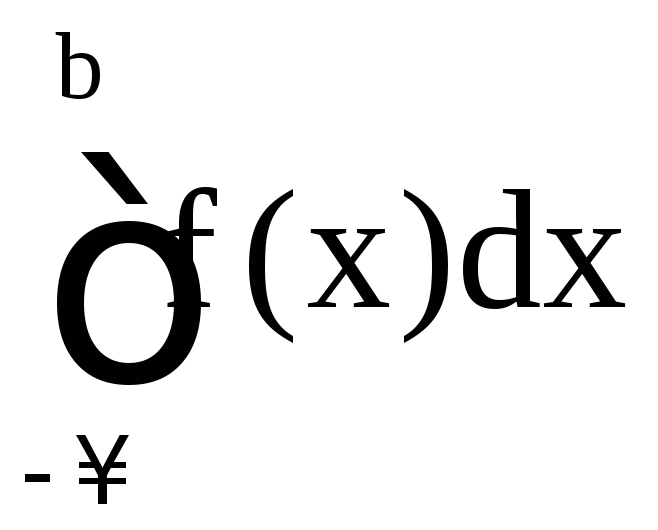 и
и
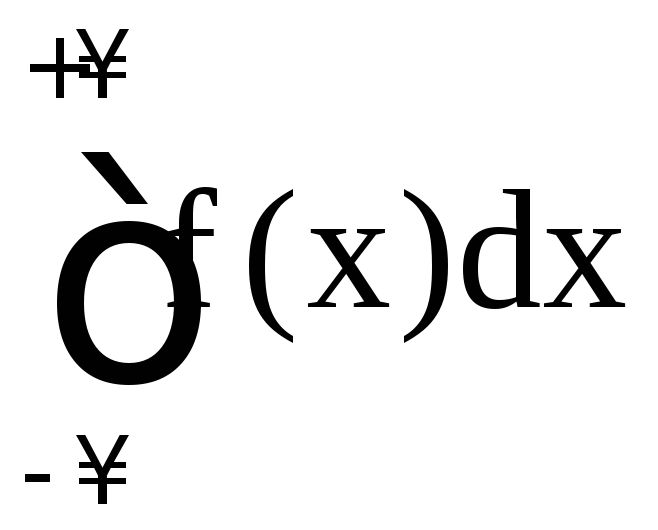 :
:
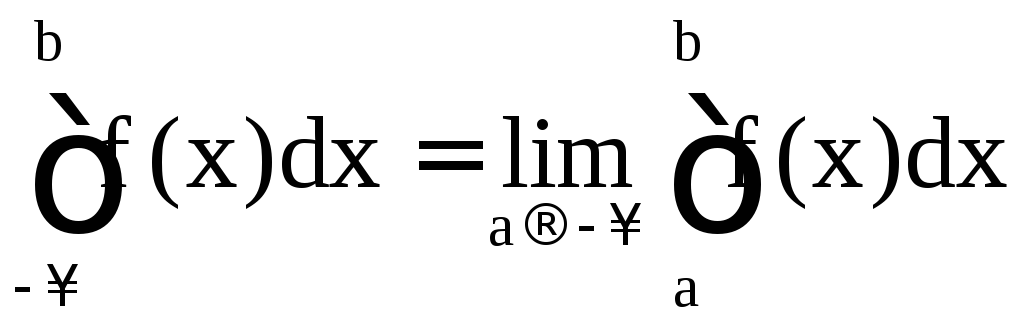 ,
,
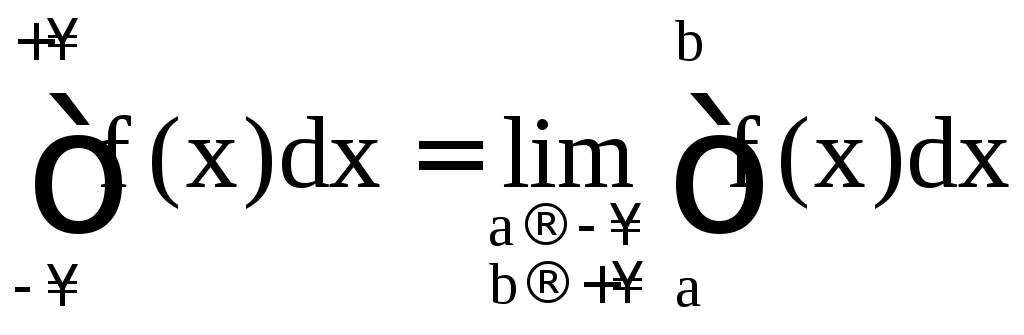 .
.
Пример
19. Вычислить:
а)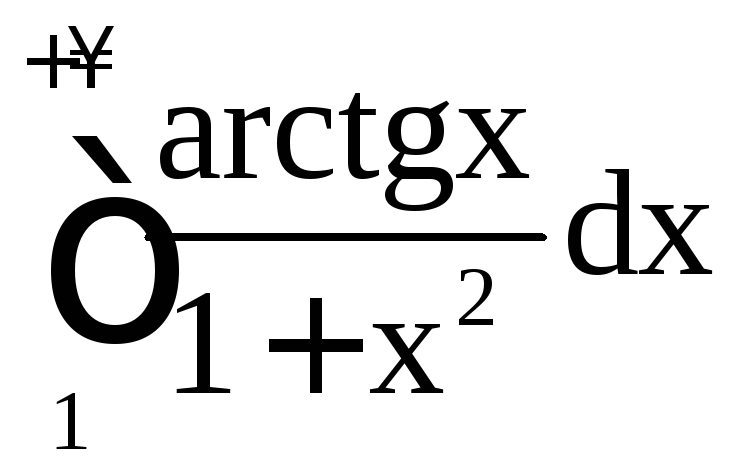 ;
б)
;
б)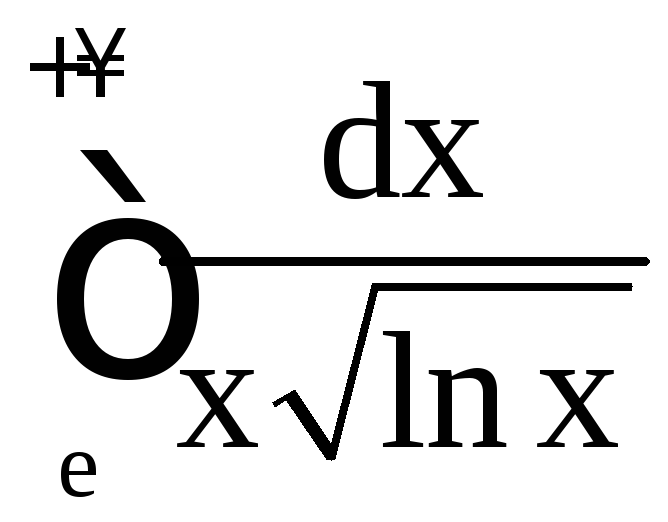 ;
в)
;
в)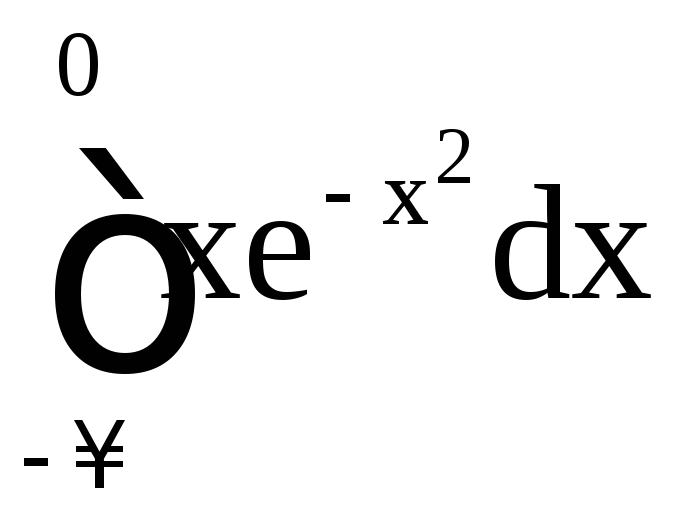 .
.
Решение.
а)
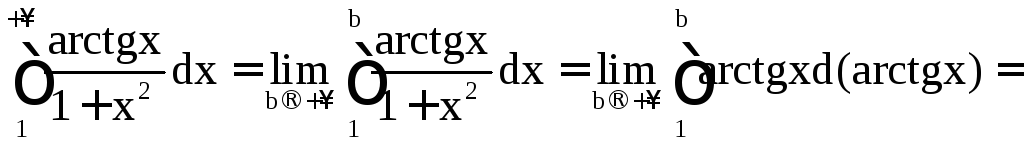
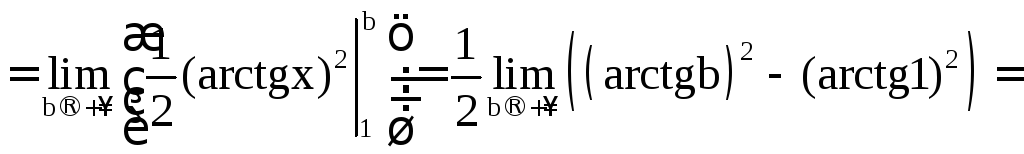
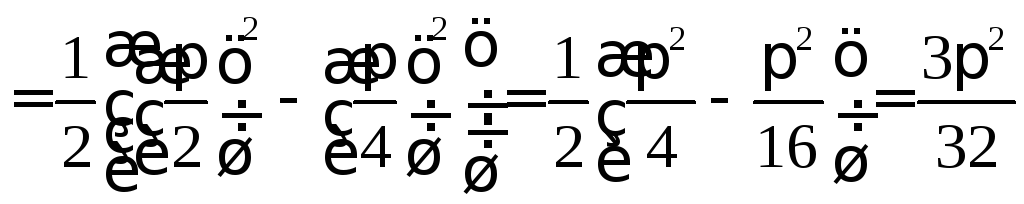 .
.
б)
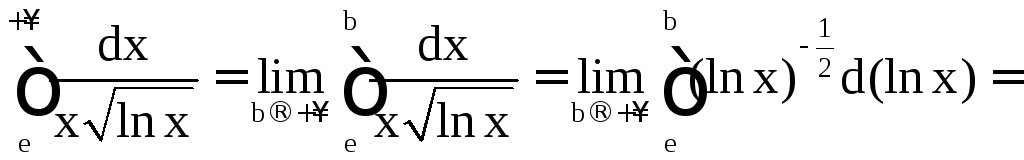
![]() ,
,
и интеграл расходится;
в)
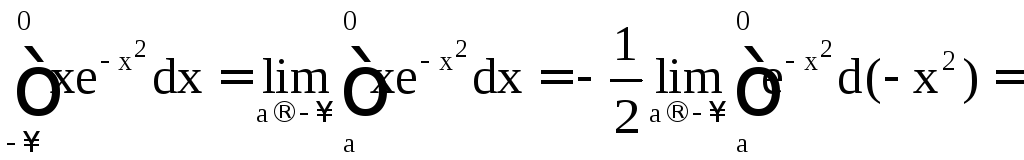
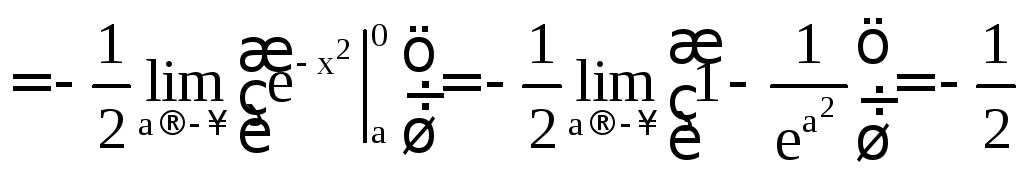 .
.
Несобственный интеграл I рода обладает свойством линейности:
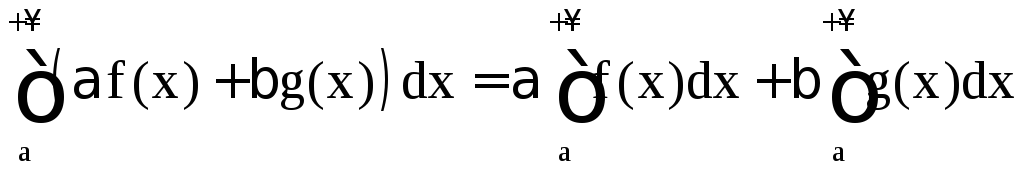
(при условии сходимости интегралов в правой части равенства).
Для исследования
вопроса сходимости несобственного
интеграла часто оказывается полезным
следующий факт: пусть
![]() ,
тогда:
,
тогда:

Аналогичное
утверждение справедливо для интеграла
![]() ,
,![]() ,
и
,
и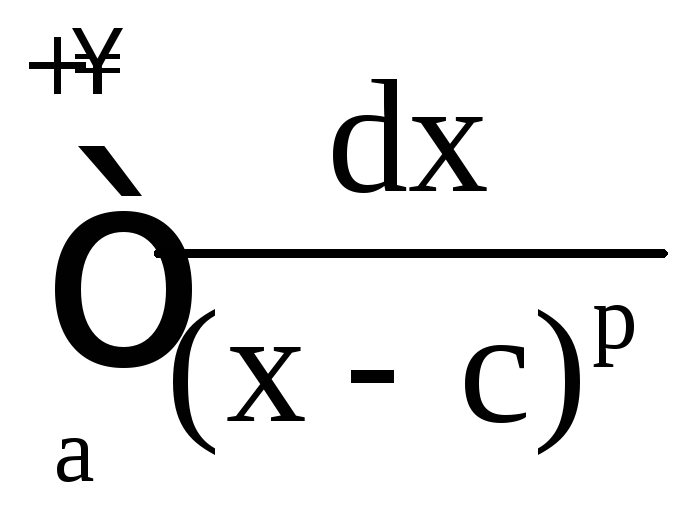 ,
a > c.
,
a > c.
Теорема 5
(первый признак сходимости).
Пусть f(x) и g(x) определены на
![]() ,
для любого b>a f(x), g(x) интегрируемы на
,
для любого b>a f(x), g(x) интегрируемы на![]() и
и![]()
![]() .
Тогда имеем:
.
Тогда имеем:
если
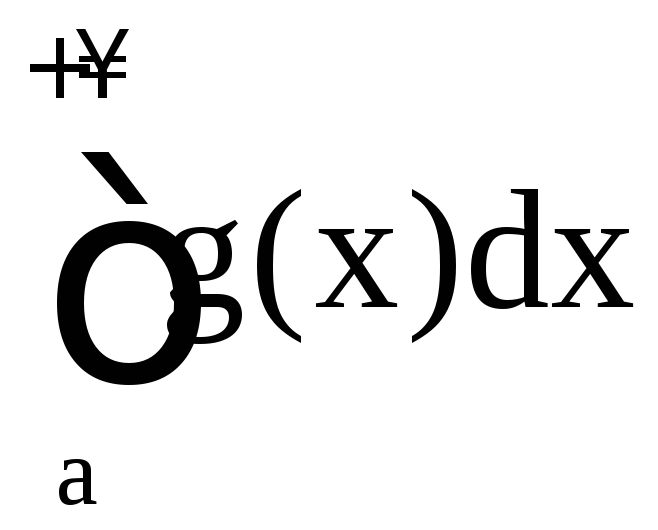 сходится, то сходится и
сходится, то сходится и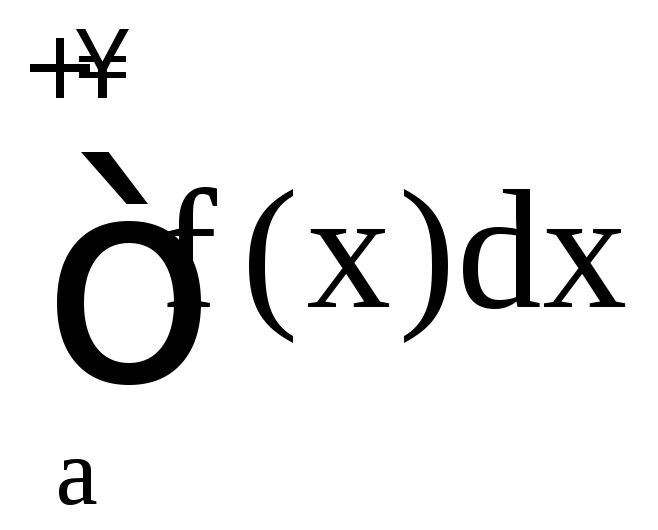 ;
;если
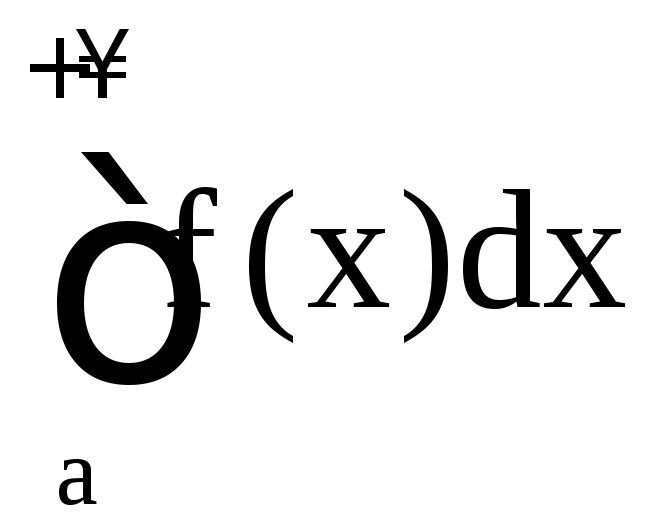 расходится, то расходится и
расходится, то расходится и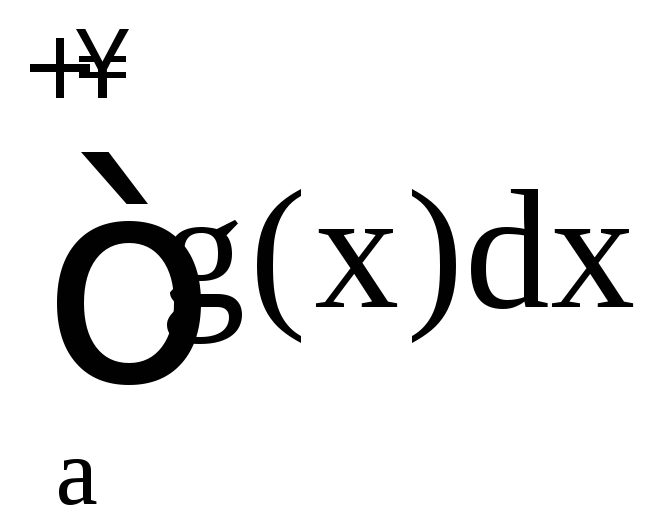 .
.
Теорема 6
(второй признак сходимости).
Пусть f(x) и g(x) определены на
![]() ,
,![]() и пусть существует конечный предел
и пусть существует конечный предел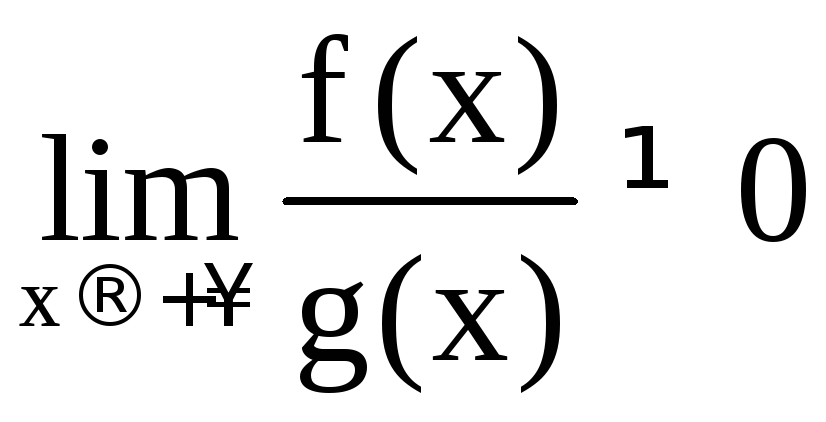 .
Тогда интегралы
.
Тогда интегралы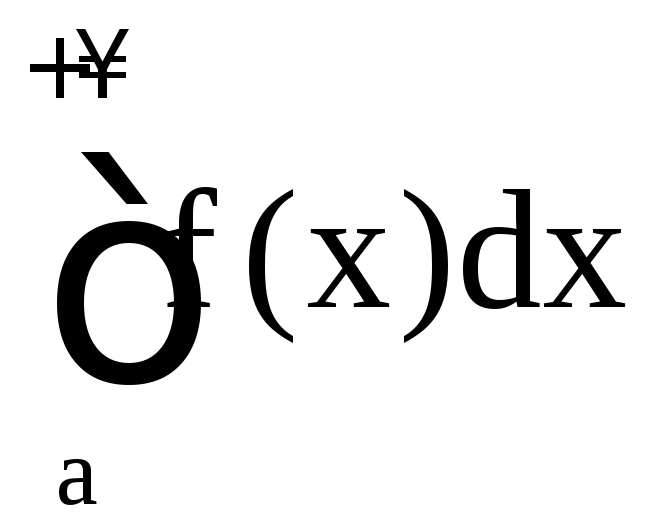 ,
,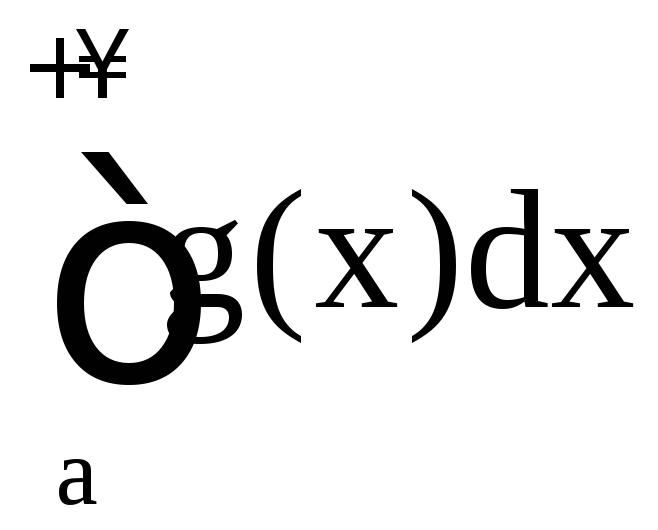 ведут себя одинаково в смысле сходимости
(т.е. одновременно сходятся или расходятся).
ведут себя одинаково в смысле сходимости
(т.е. одновременно сходятся или расходятся).
Теорема
7. Если
 сходится, то сходится и
сходится, то сходится и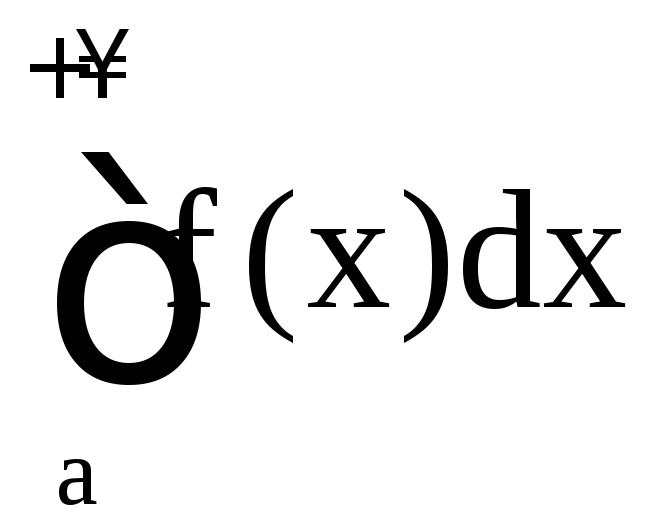
(в таком случае
говорят, что
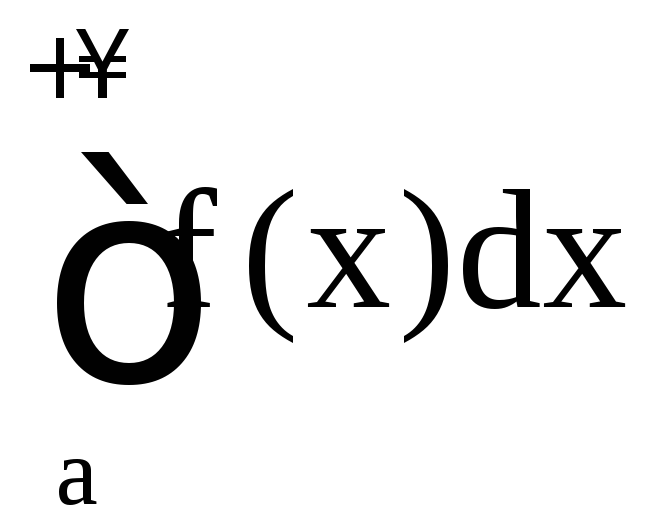 сходится абсолютно).
сходится абсолютно).
Аналогичные
утверждения справедливы для несобственного
интеграла
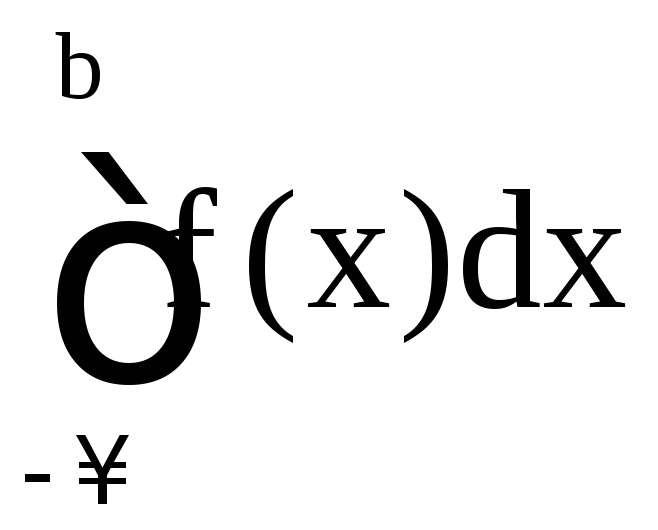 .
.
Пример 20. Исследовать на сходимость интегралы:
а)
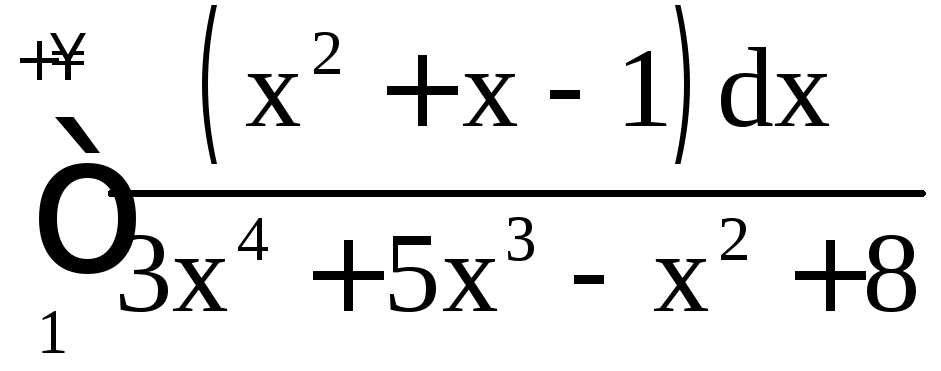 ; б)
; б)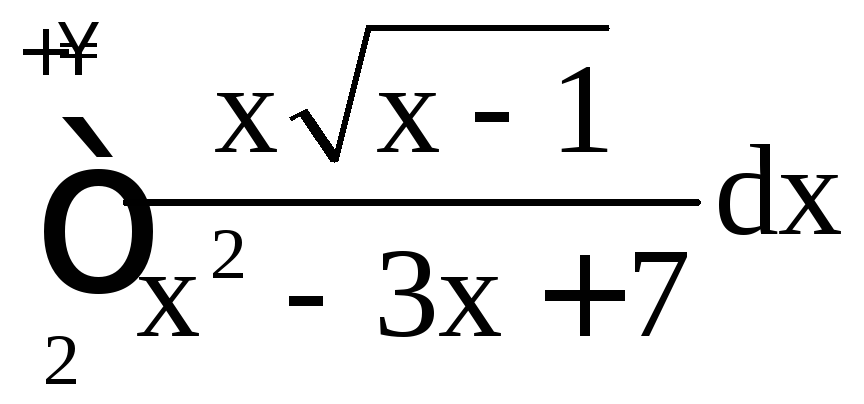 ; в)
; в)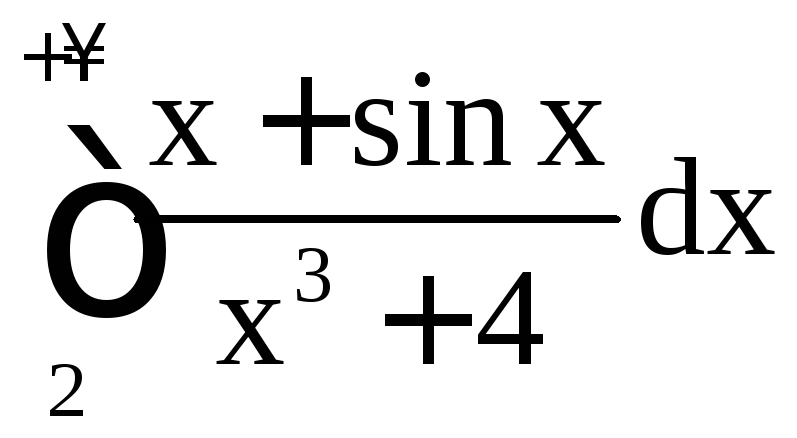 .
.
Решение.
а) Подынтегральная функция
![]() представляет собой рациональную функцию,
разность степеней числителя и знаменателя
равна 2. Рассмотрим вспомогательную
функцию
представляет собой рациональную функцию,
разность степеней числителя и знаменателя
равна 2. Рассмотрим вспомогательную
функцию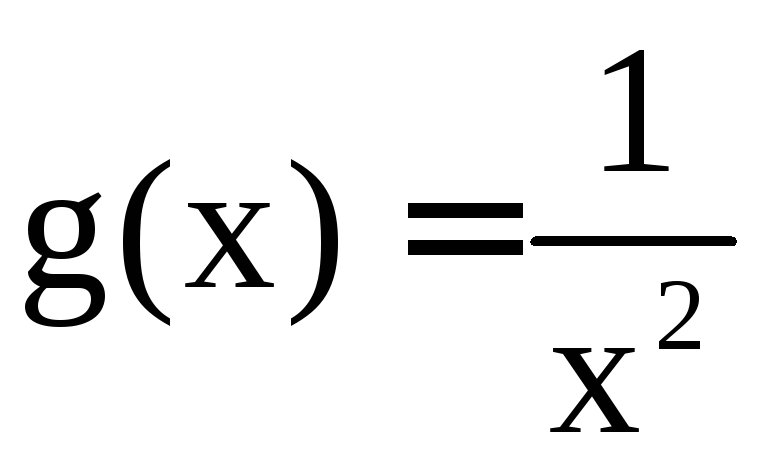 .
Найдём предел
.
Найдём предел
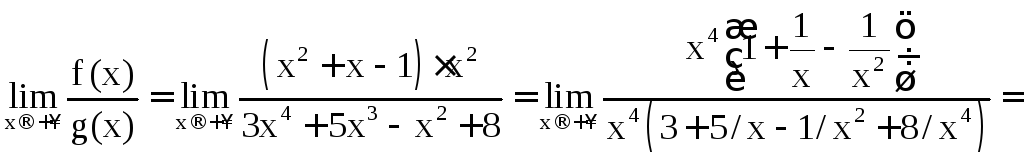
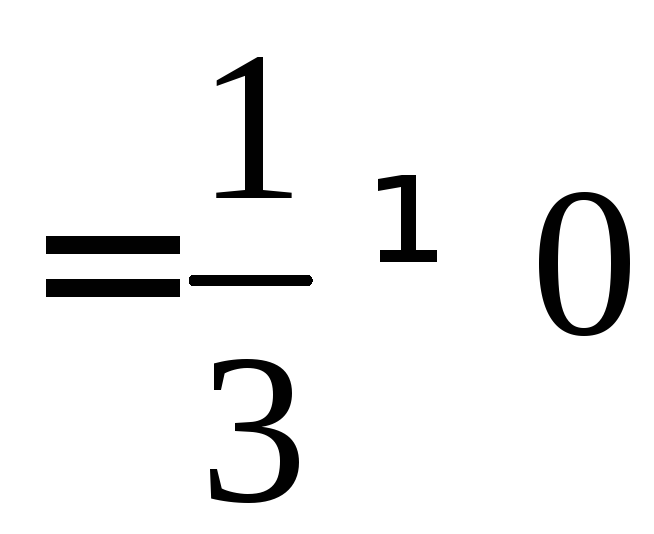 .
.
Следовательно,
согласно второму признаку сходимости,
интегралы
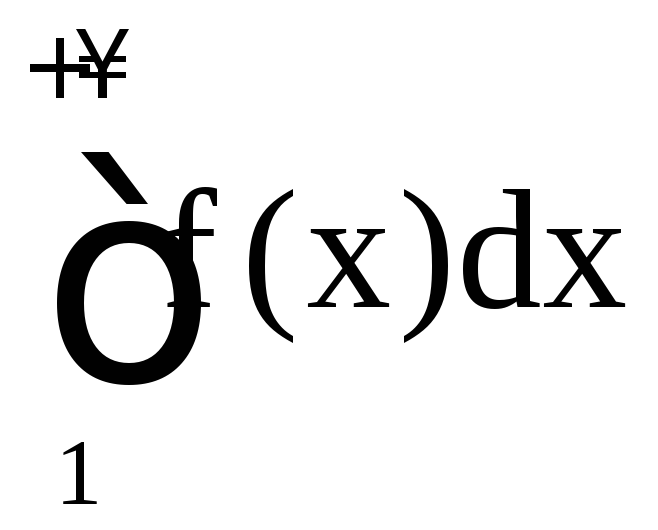 и
и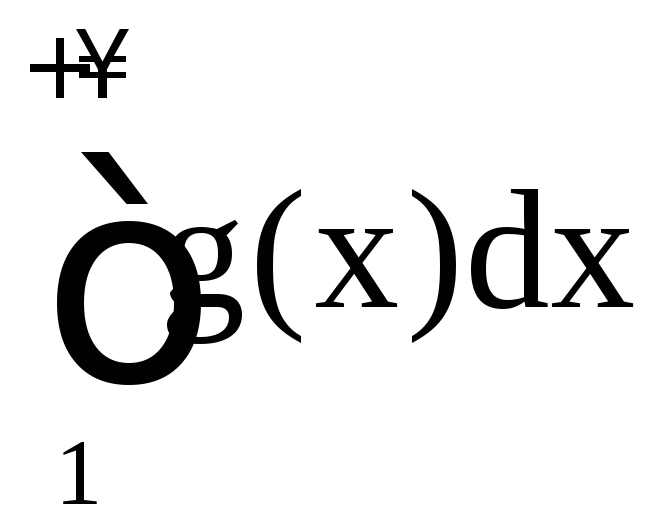 ведут себя одинаково в смысле сходимости.
Но известно, что
ведут себя одинаково в смысле сходимости.
Но известно, что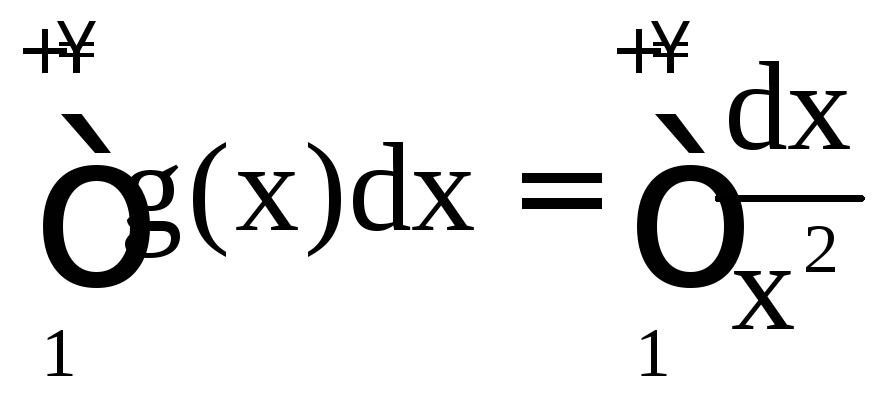 сходится
сходится![]() ,
значит и наш интеграл
,
значит и наш интеграл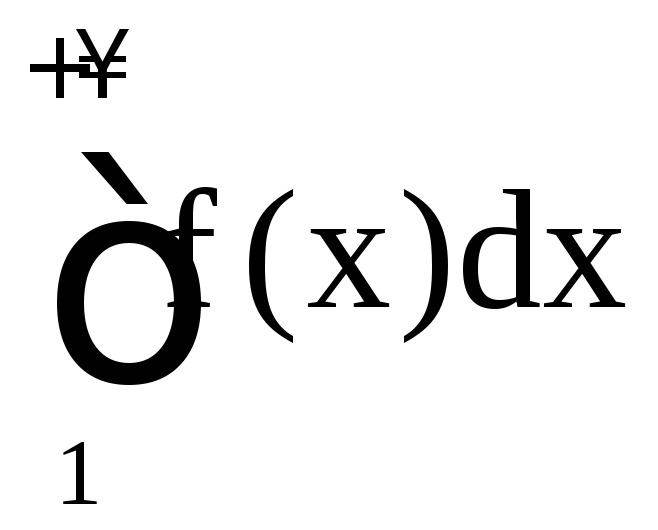 сходится.
сходится.
б)
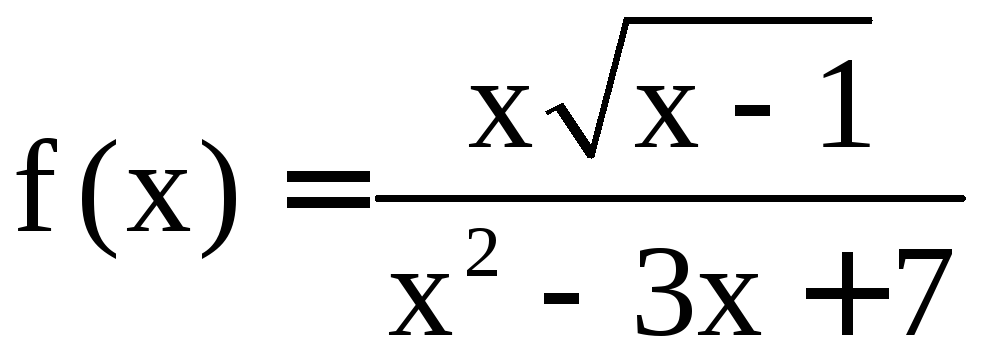 является иррациональной функцией;
степень числителя равна 3/2 (числитель
можно представить как
является иррациональной функцией;
степень числителя равна 3/2 (числитель
можно представить как![]() ),
степень знаменателя равна 2. Рассмотрим
вспомогательную функцию
),
степень знаменателя равна 2. Рассмотрим
вспомогательную функцию![]() .
Докажем, что существует конечный предел
.
Докажем, что существует конечный предел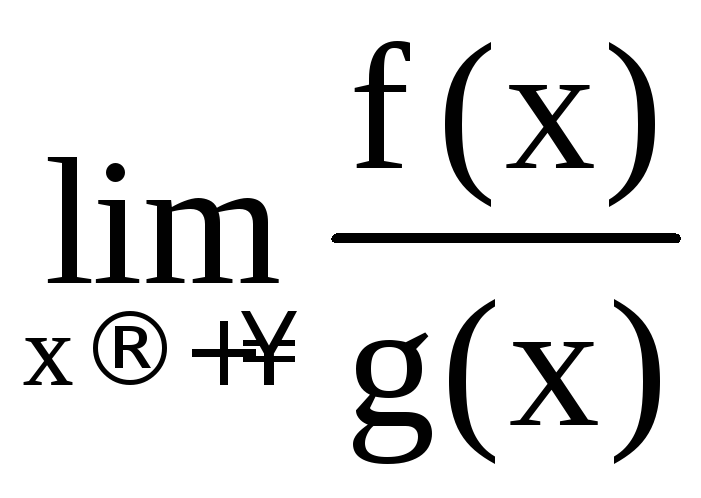 ,
не равный 0. Действительно,
,
не равный 0. Действительно,
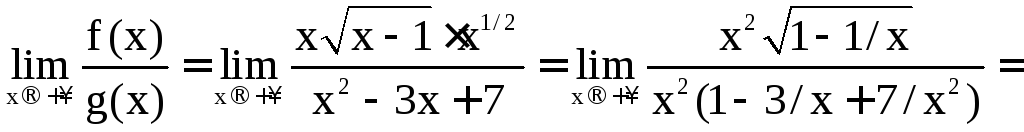
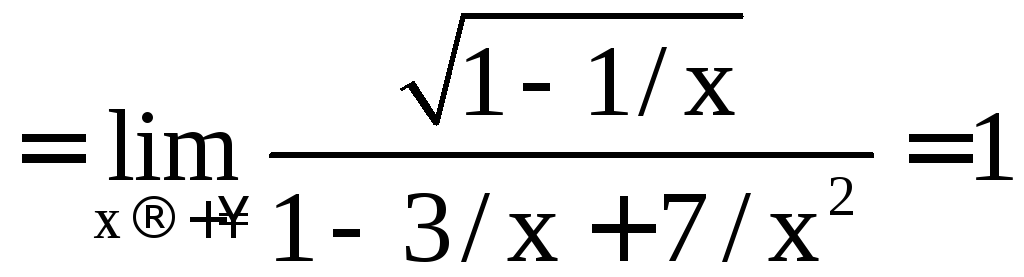 .
.
Поэтому
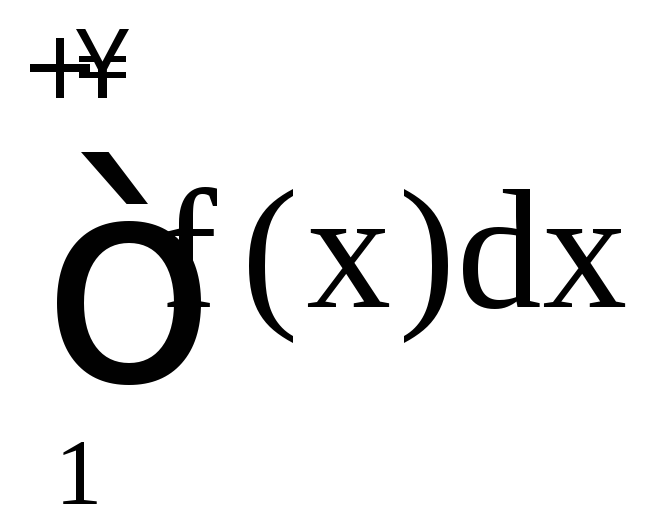 ,
,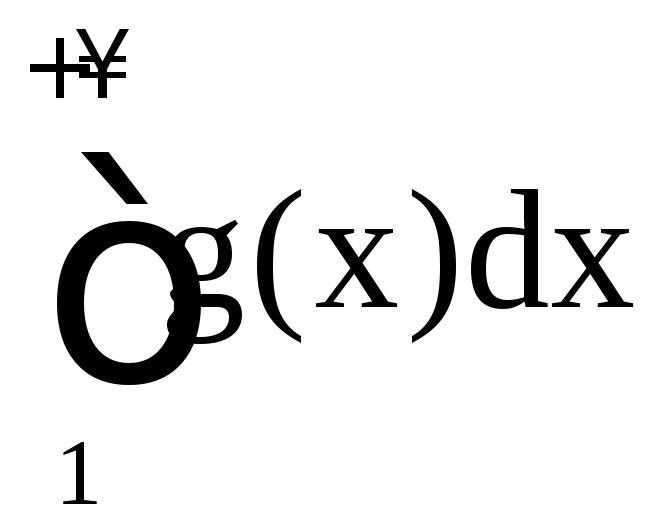 ведут себя одинаково в смысле сходимости.
А так как
ведут себя одинаково в смысле сходимости.
А так как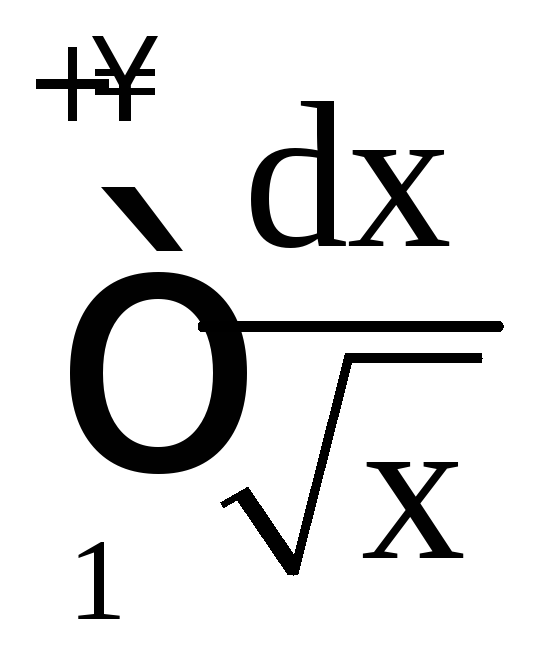 расходится, то расходится и
расходится, то расходится и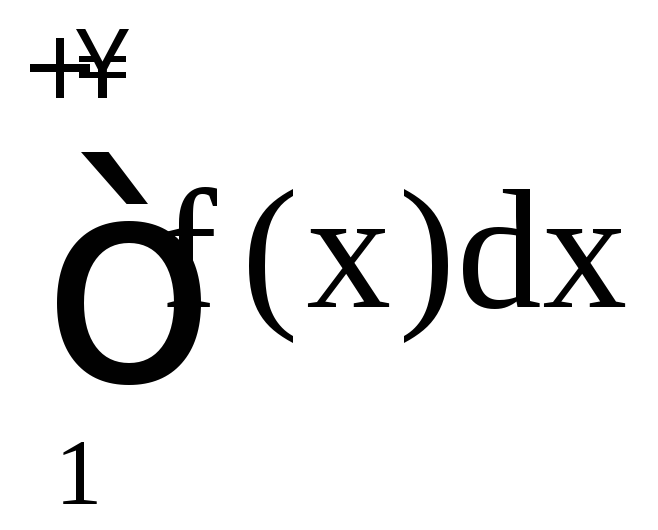 .
.
в) Обозначим
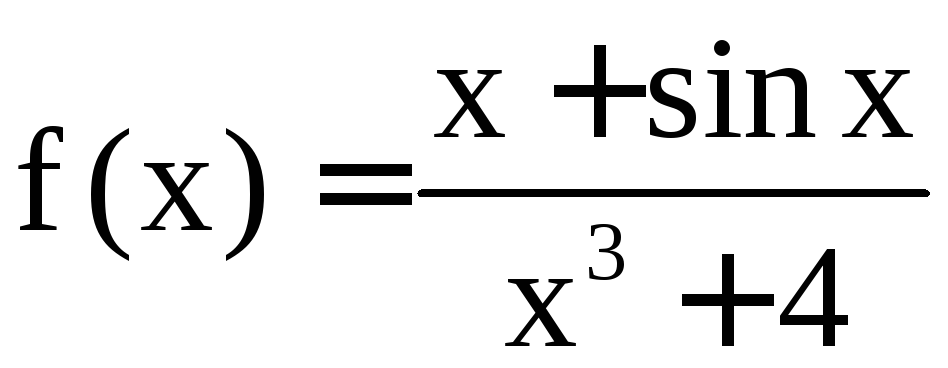 .
Так как
.
Так как![]() ,
то
,
то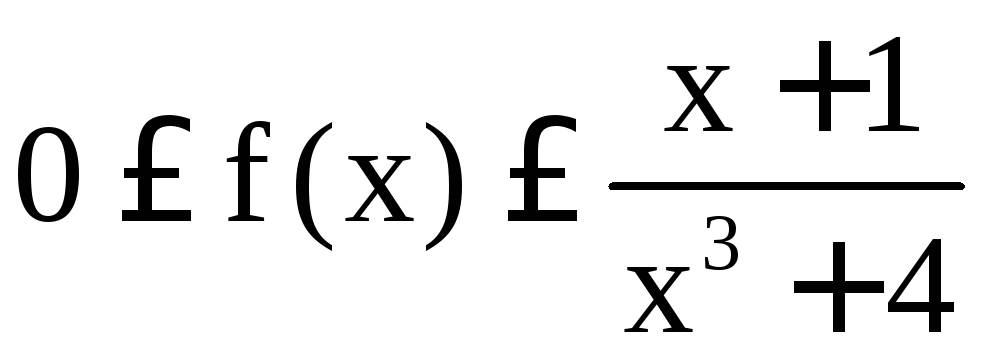 .
Интеграл
.
Интеграл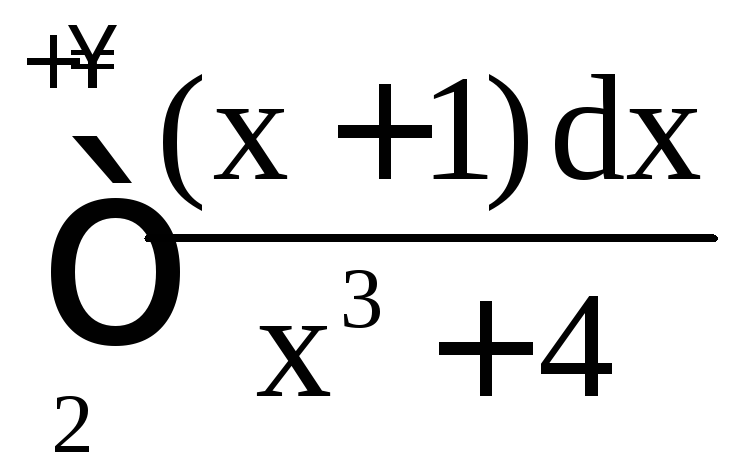 сходится (доказывается это, как и выше:
сходится (доказывается это, как и выше: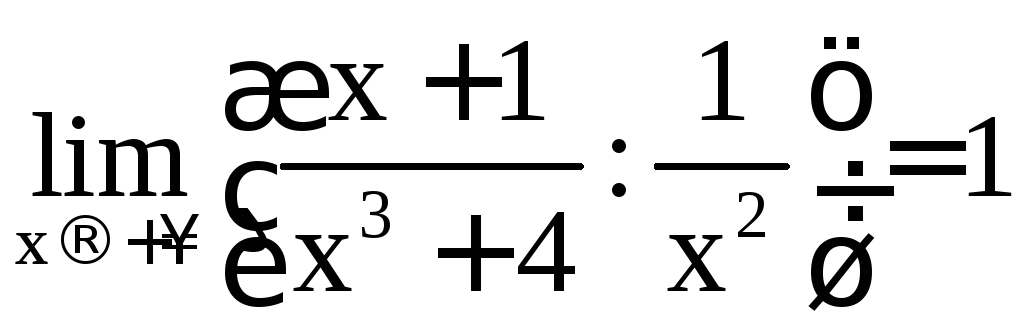 ,
,![]() сходится и можно воспользоваться вторым
признаком сходимости). Мы попадаем в
условие теоремы 5 (часть 1), в которой
говорится, что наш интеграл сходится.
сходится и можно воспользоваться вторым
признаком сходимости). Мы попадаем в
условие теоремы 5 (часть 1), в которой
говорится, что наш интеграл сходится.
2. Несобственный
интеграл II рода. Пусть
функция f(x) определена на [a; b) и
![]() (или = –).
Несобственный интеграл второго рода
функции f(x) на [a; b
определяется равенством
(или = –).
Несобственный интеграл второго рода
функции f(x) на [a; b
определяется равенством
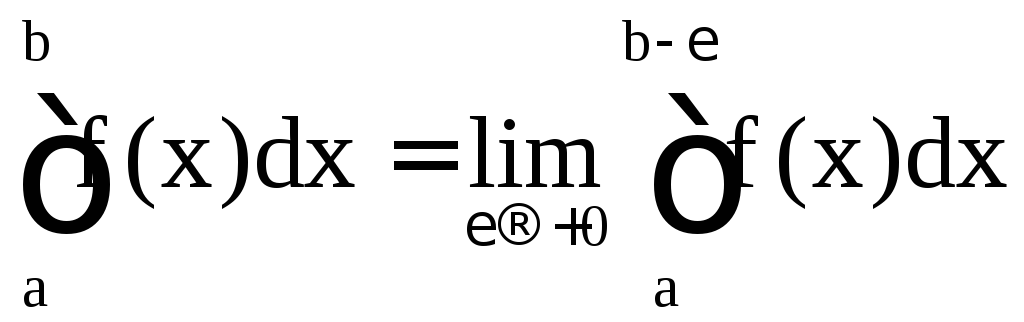 .
.
Если существует
конечный предел в этом равенстве, то
говорят, что интеграл
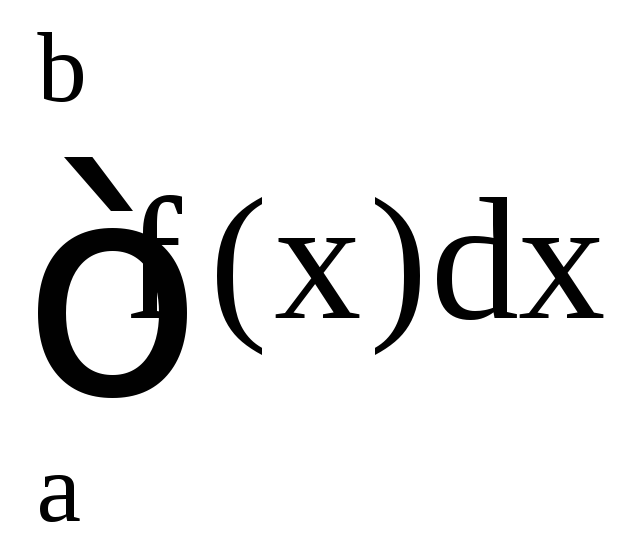 сходится, в противном случае – расходится.
Аналогично определяется несобственный
интеграл II рода для случаев
сходится, в противном случае – расходится.
Аналогично определяется несобственный
интеграл II рода для случаев![]() и
и![]() .
Если же f(x) неограниченна в любой
окрестности некоторой внутренней точки
.
Если же f(x) неограниченна в любой
окрестности некоторой внутренней точки![]() ,
то полагают
,
то полагают
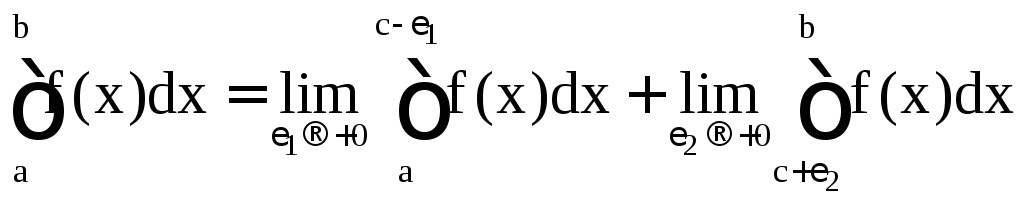 .
.
Пример
21. Вычислить
интегралы: а)
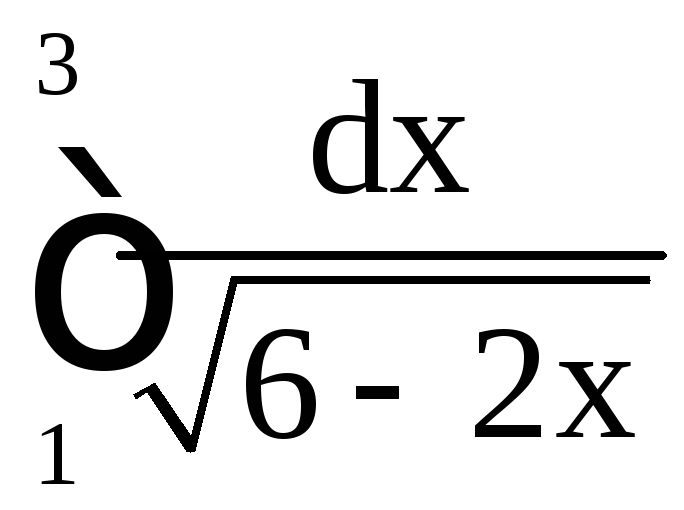 ;
б)
;
б)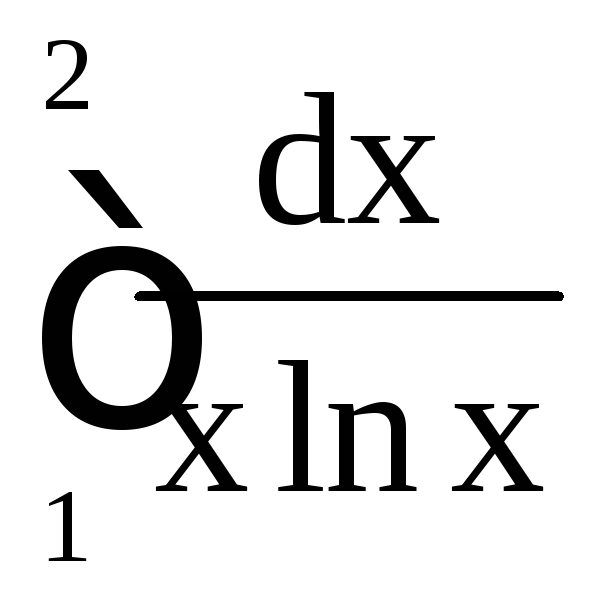 .
.
Решение.
а)
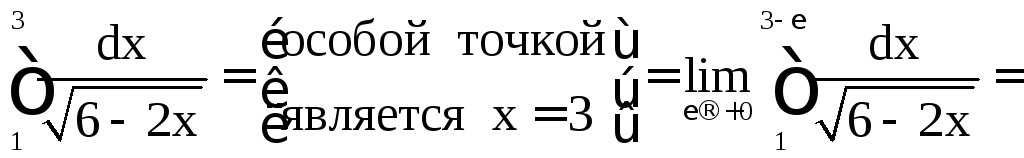
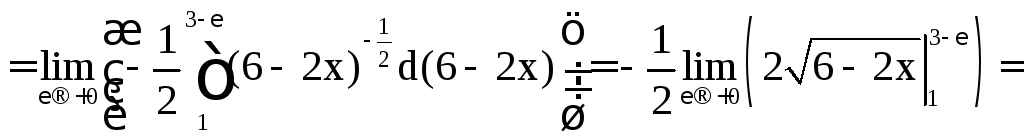
![]() .
.
б)
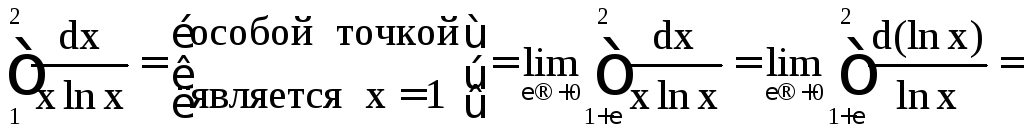
![]() .
.
Значит, интеграл расходится.
Формулировки признаков сходимости для несобственных интегралов II рода, по существу, ничем не отличаются от формулировок признаков сходимости для несобственных интегралов I рода. Для применения этих признаков полезно пользоваться тем, что
 ,
,
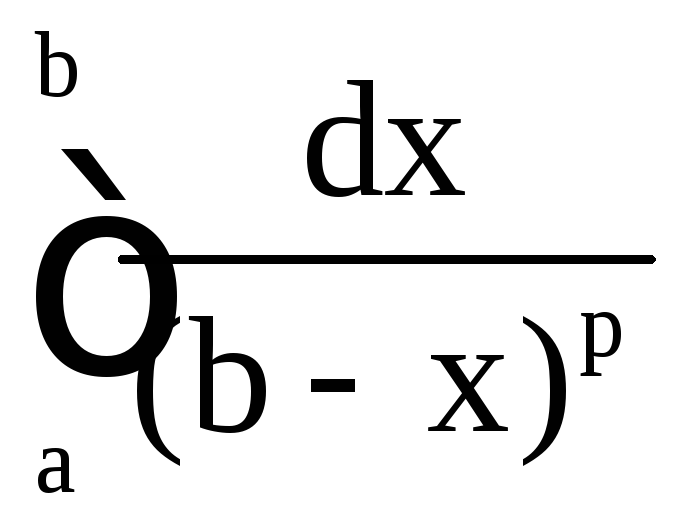

Пример 22. Исследовать на сходимость интегралы:
а)
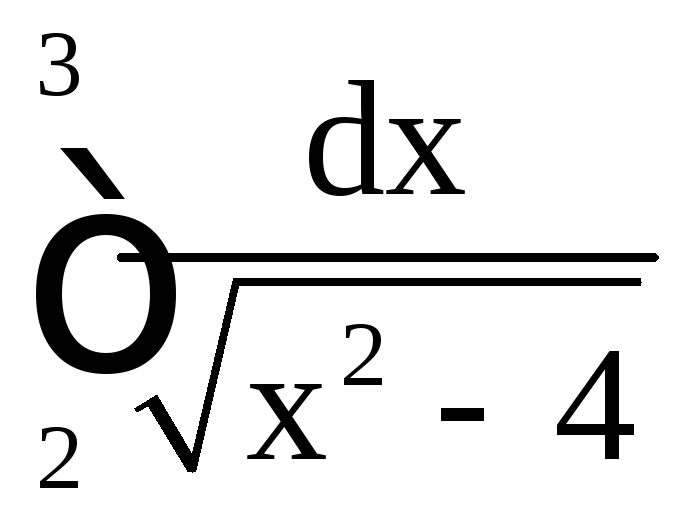 ;
б)
;
б)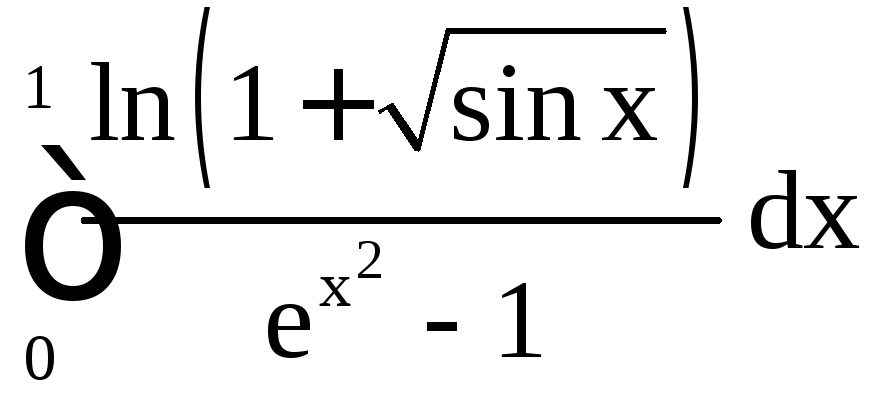 ; в)
; в)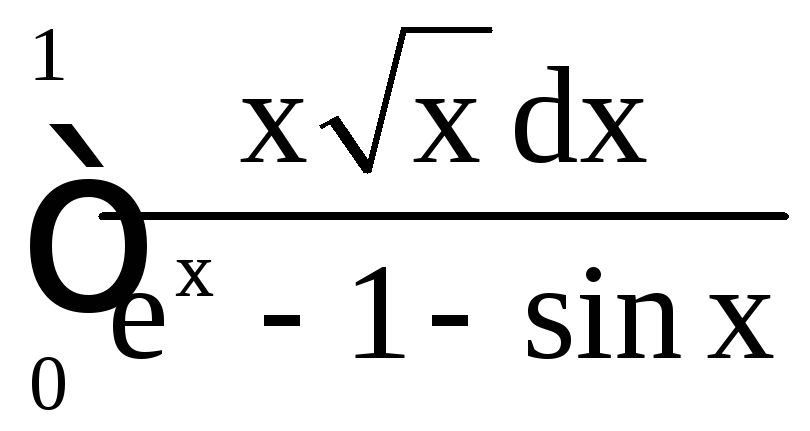 .
.
Решение.
а)
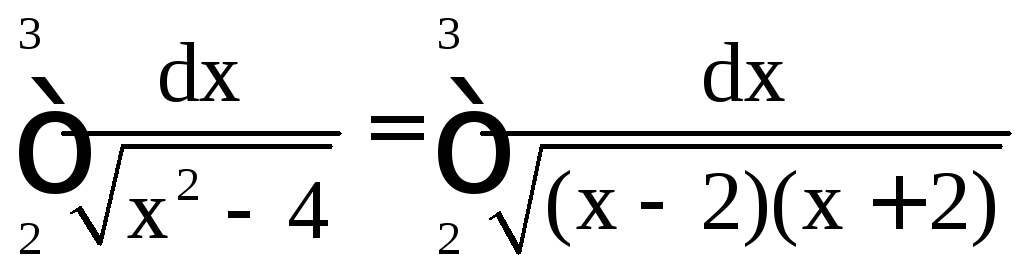 .
Подынтегральная функция
.
Подынтегральная функция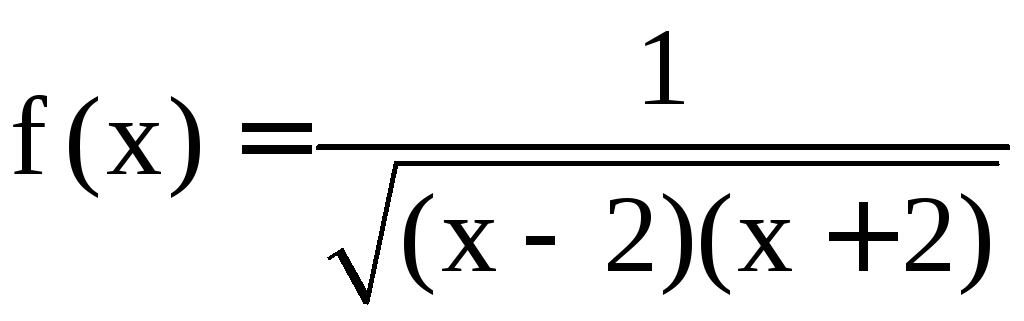 в промежутке [2; 3] имеет особую точку x
= 2. Множитель
в промежутке [2; 3] имеет особую точку x
= 2. Множитель стремится к 1/2 при
стремится к 1/2 при![]() .
Поэтому естественно ожидать, что наша
функция в окрестности точки x = 2 ведёт
себя, как
.
Поэтому естественно ожидать, что наша
функция в окрестности точки x = 2 ведёт
себя, как![]() ;
проверим это:
;
проверим это:
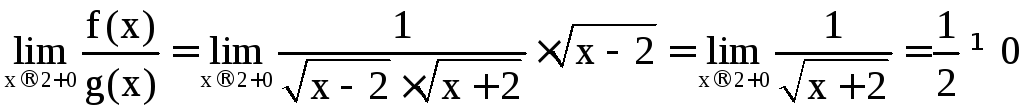 .
.
Следовательно,
согласно второму признаку сходимости,
интегралы
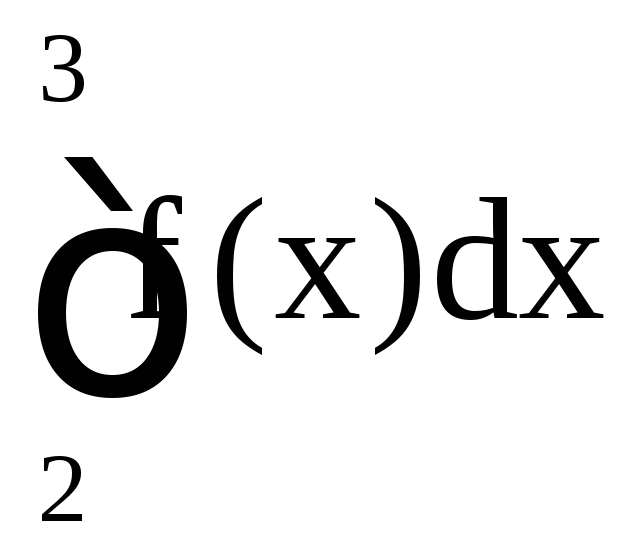 и
и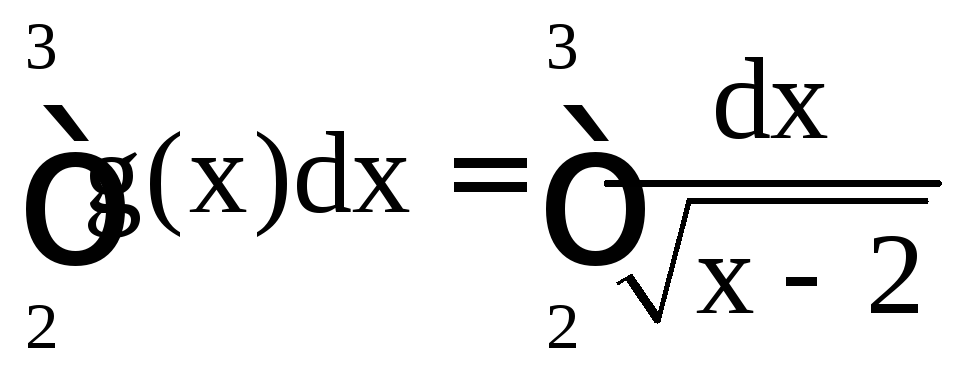 ведут себя одинаково в смысле сходимости.
Но второй интеграл сходится (p = 1/2 < 1),
поэтому сходится и наш интеграл.
ведут себя одинаково в смысле сходимости.
Но второй интеграл сходится (p = 1/2 < 1),
поэтому сходится и наш интеграл.
б) Функция
![]() имеет на промежутке [0; 1] одну особую
точку x = 0. Функции
имеет на промежутке [0; 1] одну особую
точку x = 0. Функции![]() и
и![]() являются бесконечно малыми величинами
при
являются бесконечно малыми величинами
при![]() .
Известно, что
.
Известно, что![]()
![]()
![]() ,
,![]()
x2
при
x2
при
![]() .
Поэтому
.
Поэтому![]()
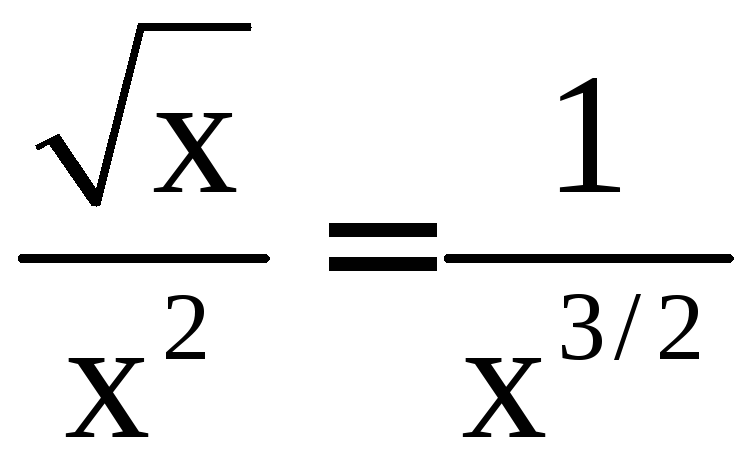 при
при![]() .
А так как
.
А так как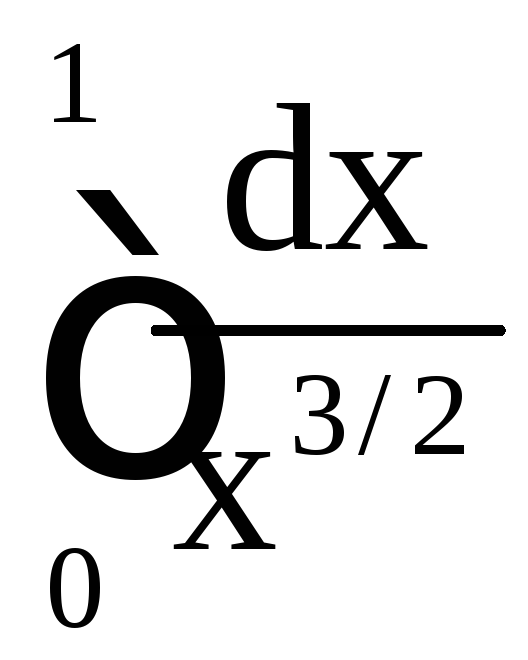 расходится
расходится![]() ,
то расходится и наш интеграл.
,
то расходится и наш интеграл.
в) Разложим
знаменатель (![]() )
подынтегральной функции
)
подынтегральной функции![]() по формуле Тейлора в окрестности особой
точки
по формуле Тейлора в окрестности особой
точки![]() функции
функции![]() :
:
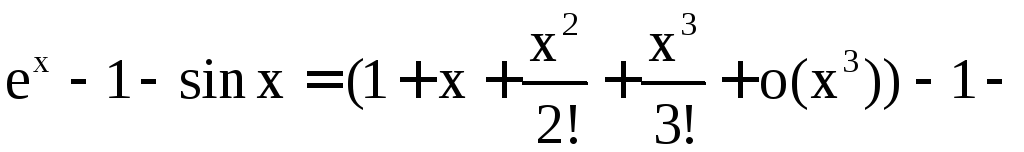
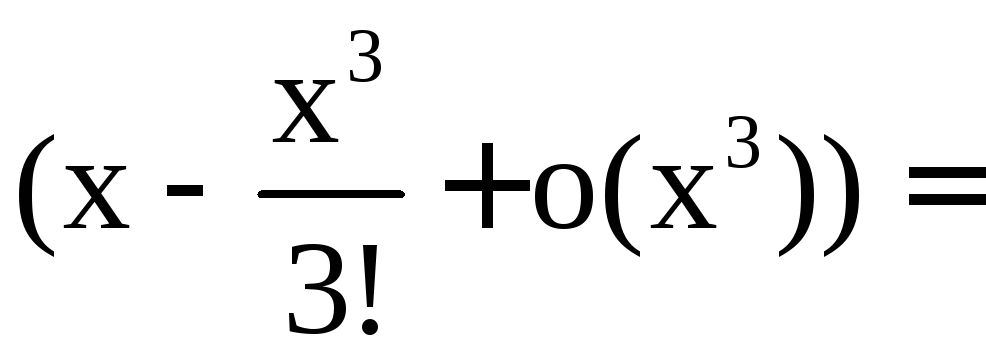
![]() .
.
Следовательно,
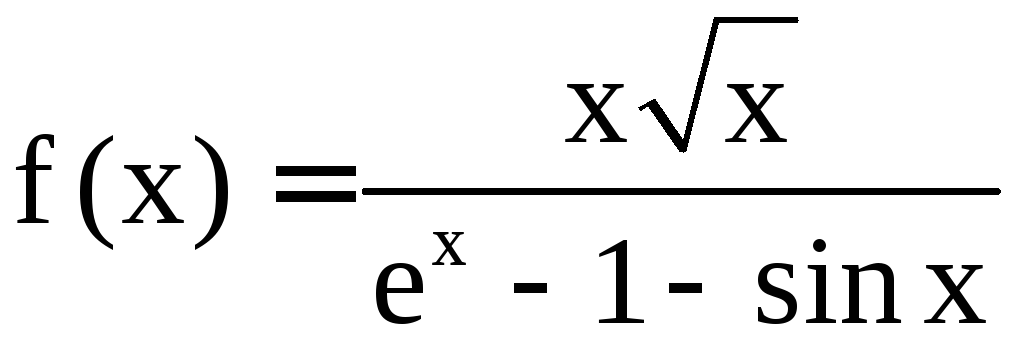
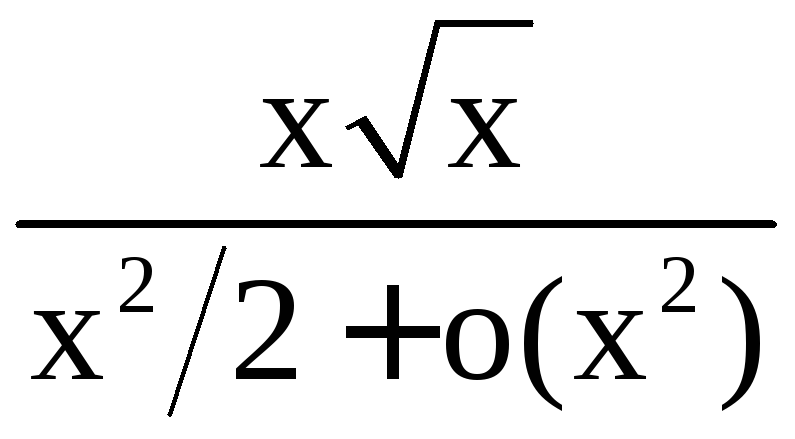
![]() .
.
Известно, что
![]() сходится, следовательно, сходится и наш
интеграл.
сходится, следовательно, сходится и наш
интеграл.
