Prtakt_fiz_him-och

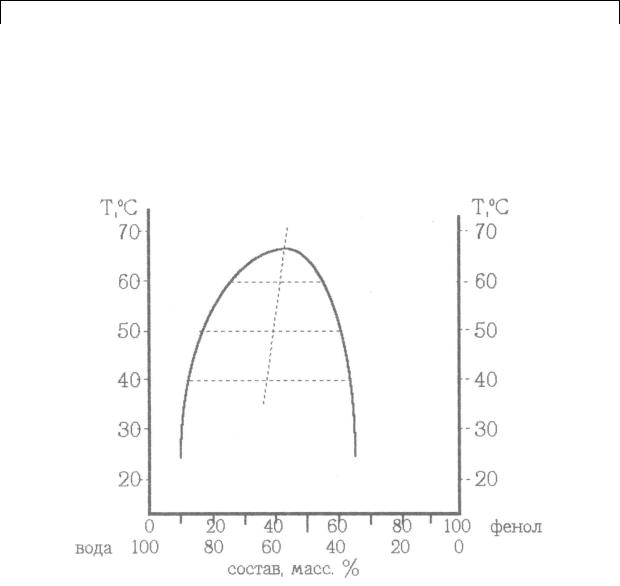
через экспериментальные точки. Указать на ней области существования гомогенных и гетерогенных смесей.

15.Провести конноды, отвечающие температурам 40, 45, 50, 60, 65оС (или другим, указанным преподавателем), как показано на рисунке. Определить составы сопряжѐнных растворов при температурах, указанных преподавателем.

16.Найти и отметить точки, отвечающие среднему арифметическому из составов сопряжѐнных фаз, которые находятся точно в середине каждой конноды. Провести прямую линию, соединяющую середины коннод, и продлить еѐ до пересечения с кривой расслоения. Определить критическую температуру растворения системы. Установить, подчиняется ли данная система правилу Алексеева.

17.Занести расчетные данные в таблицу.

Температура, оС

18. Сформулировать выводы.

61

Работа 2.4. Определение коэффициента распределения третьего компонента между двумя жидкими фазами.

Цель работы: Определение коэффициента распределения третьего компонента между водой и органическим растворителем путем про-

ведения жидкостной экстракции.

Целевые задачи: Проведение жидкостной экстракции третьего ком-

понента из водного раствора органическим растворителем; титри-

метрическое определение концентрации третьего компонента в обеих фазах системы; расчет коэффициента распределения и степени ассоциации вещества в органическом растворителе; оценка экстрак-

ционной эффективности органического растворителя.

Если в систему из двух несмешивающихся жидкостей ввести не-

большое количество третьего компонента, то после установления равнове-

сия он окажется в обеих фазах, но в разном количестве. Для каждой

температуры отношение концентраций третьего компонента в двух равновесных жидких фазах является величиной постоянной, незави-

симо от этих концентраций (закон распределения Нернста):

С1

= К

С2

где К коэффициент распределения.

Закон распределения является теоретической основой жидкостной экстракции. Экстракцией из растворов называется извлечение и разделе-

ние компонентов раствора путем перевода их из одной жидкой фазы в дру-

гую, содержащую экстрагент. Основными условиями экстракции являются:

а) несмешиваемость экстрагента с исходным раствором,

62

б) отсутствие химического взаимодействия извлекаемого вещества с экст-

рагентом,

в) лучшая растворимость извлекаемого вещества в экстрагенте, чем в пер-

воначальном растворителе.

Фаза, в которую после экстракции переходит извлекаемое вещество,

называется экстрактом, а фаза, обедненная им рафинатом.

Количественной характеристикой эффективности экстракции явля-

ется коэффициент распределения. В данных методических указаниях вы-

брана такая система обозначений: С1 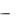концентрация извлекаемого вещества в рафинате, С2 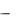его концентрация в экстракте. При этом чем меньше значение коэффициента распределения, тем эффективнее экстра-

гент и тем больше степень извлечения третьего компонента. Она опреде-

ляется как отношение массы извлекаемого вещества в экстракте к его массе, содержавшейся в исходном растворе до экстракции.

В ряде случаев при переходе третьего компонента через поверхность раздела фаз его средняя молярная масса изменяется вследствие ассоциа-

ции или диссоциации в одном из растворителей. В таких случаях уравне-

ние закона распределения можно представить в виде С1

С2n

где n - показатель при данной температуре, обусловленный свойствами всех трех компонентов системы, и представляющий собой отношение средних молярных масс третьего компонента в экстрагенте и в исходном растворителе. Например, если уксусная кислота в воде существует глав-

ным образом в виде отдельных молекул, а в бензоле - в виде ассоциатов из двух молекул (димеров), то:

63

Чаще других используют графический метод определения К. Его принцип заключается в следующем. Уравнение (1) путем логарифмирова-

ния преобразуется в уравнение прямой, не проходящей через начало коор-

динат:

lgC1 = lgK + n lgC2 .

Затем по экспериментальным данным строится график зависимости lgC1 от lgC2, отсекающее от оси ординат отрезок, равный lgK. Тангенс угла наклона этого графика к оси абсцисс равен n. (подробнее об этом см. «Проведение опыта»).

тягой! После окончания работы категорически запрещается сливать их в канализацию. Для этого имеется специальный сосуд в вытяжном шкафу.

Проведение опыта

1.Проверить оснащение рабочего места.

2.Измерить и записать температуру.

3.В три склянки с притертыми пробками поместить по 10 мл водных рас-

творов экстрагируемого вещества кислотной природы (по указанию преподавателя).

4.Добавить к каждому раствору по 10 мл указанного преподавателем ор-

ганического растворителя (под тягой!).

64

5.Склянки плотно закрыть пробками и после интенсивного встряхивания в течение трех минут оставить для перераспределения не менее чем на 20

минут.

6.Определить титрованием концентрацию экстрагируемого вещества во всех исходных растворах (обозначается С0I, С0II и С0III) для чего отмерить

1 мл исходного раствора экстрагируемого вещества в колбу для титро-

вания, затем добавить 1 каплю раствора фенолфталеина и титровать 0,1

н. раствором NaOH до появления слабо-розового окрашивания, не исче-

зающего в течение 30 - 40 секунд. Повторить титрование трижды для каждого раствора. Рассчитать С0I, С0II и С0III по уравнению:

СщVщ

Vк

где Vщ - объѐм раствора NaOH, пошедший на титрование (среднее арифметическое из результатов трех титрований), Cщ - концентрация

NaOH, моль-экв/л, Vк - объѐм раствора экстрагируемого вещества,

взятый для титрования (в данном случае – 1 мл).

Данные занести в таблицу 1.

7.После установления экстракционного равновесия определить равновес-

ные концентрации экстрагируемого вещества С1I, С1II и С1III в водном слое (рафинате). Для этого из склянок отобрать пипеткой по 1 мл вод-

ных растворов экстрагируемого вещества (нижний слой) в колбы для титрования и оттитровать 0,1 н. раствором NaOH. Титрование провести трижды для каждого раствора (все результаты титрования сверить у преподавателя). Для расчета использовать уравнение (2).

8.По разности С0 – С1 = С2 вычислить равновесные концентрации экстра-

гируемого вещества С2I, С2II и С2III в органическом слое (экстракте).

Данные сверить у преподавателя и занести в таблицу 1.

9.Рассчитать логарифмы С1 и С2 (с точностью до четырех десятичных

65

знаков) и занести данные в таблицу 1.

Таблица 1.

№ V0 щ C0 V1 щ C1 lgC1 C2 lgC2 K=C1/C2n

п.п.

1

2

3

Kсредн=

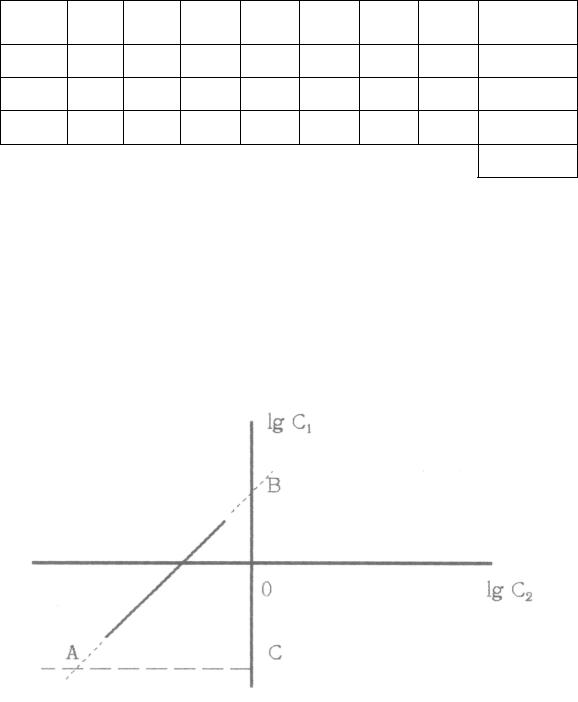
11. Построить график зависимости lgC1 от lgC2 (см. рис.) и продлить его до пересечения с осью Y. При этом от неѐ отсекается отрезок ОВ, равный lgК, а тангенс угла наклона графика к оси Х равен n. Рассчитать коэффициент распределения К=10ОВ. Построить прямоугольный треугольник АВС (так, чтобы отрезки ВС и АС были как можно больше для повышения точности расчета). Рассчитать степень ассоциации экстрагируемого вещества в экстрагенте n = BC/AC.

66

Тема 3. Кондуктометрия

Кондуктометрия – физико-химический метод исследования и анали-

за различных систем (главным образом водных растворов), основанных на измерении электрической проводимости. Кондуктометрический метод по-

зволяет:

-определить наличие или отсутствие диссоциации исследуемого вещест-

ва в растворе;

-термодинамические характеристики электролитической диссоциации вещества (в частности, энергию диссоциации);

-растворимость трудно растворимых соединений;

-степень и константу диссоциации слабых электролитов;

-константы устойчивости комплексных ионов .

Зависимость электрической проводимости растворов от концентра-

ции веществ лежит в основе одного из методов количественного анализа -

кондуктометрического титрования.

Кондуктометрический метод применяется для фармацевтического анализа лекарственных веществ, для описания свойств новых веществ (как синтезированных, так и выделенных из растительного сырья), для изуче-

ния термодинамики и кинетики биохимических и физиологических про-

цессов, связанных с проницаемостью биологических мембран, со свойствами аминокислот, белков и других, способных к ионизации соеди-

нений.

Изучив данную тему и выполнив лабораторные работы, относящиеся к ней, студент должен знать:

свойства растворов электролитов;

теорию электролитической диссоциации;

основные положения теории растворов сильных электролитов Дебая– Хюккеля;

68

закон разведения Оствальда, закон Кольрауша;

расчетные формулы используемых кондуктометрических методов;

устройство и принцип работы кондуктометра.

Студент должен уметь:

измерять электрическое сопротивление растворов электролитов с по-

мощью кондуктометра;

рассчитывать константу ячейки кондуктометра;

определять удельную и эквивалентную электрические проводимости,

степень и константу диссоциации (ионизации) электролитов;

проводить кондуктометрическое титрование;

строить и анализировать кривые кондуктометрического титрования.

Студент должен приобрести или закрепить навыки:

приготовления, разбавления и отмеривания растворов;

расчета концентрации веществ в растворах;

титрования;

заполнения таблиц, построения и анализа графиков;

пользования справочной литературой.

Вопросы для самоподготовки.

1.Электрохимия. Основные понятия. Электролитическая диссоциация.

Теория растворов сильных электролитов Дебая-Хюккеля. Ионная сила растворов.

2.Коллигативные свойства (криоскопия, эбулиоскопия, осмотическое дав-

ление) растворов электролитов. Изотонический и осмотический коэф-

фициенты, их расчет.

3.Электролитическая диссоциация воды. Водородный показатель рН как мера активной реакции среды.

69

4.Активность ионов и еѐ связь с концентрацией электролита. Коэффици-

ент активности. Константа диссоциации слабых электролитов. Степень диссоциации. Закон разведения Оствальда. Вывод его математического выражения.

5.Удельная и эквивалентная (мольная) электрическая проводимость рас-

творов. Зависимость электропроводимости от различных факторов.

Подвижность ионов. Закон Кольрауша.

6.Кондуктометрическое определение степени и константы диссоциации слабых электролитов.

7.Кондуктометрическое титрование.

Решение типовых задач

Задача 1. Удельная электрическая проводимость 0,175 М раствора аммиака равна 0,476 Ом 1см 1. Подвижности ионов NH4+ и ОН– при 25оС

соответственно равны 73,5 и 198,3 Ом 1см2моль 1. Рассчитать молярную проводимость, степень и константу ионизации аммиака рКb, концентрацию ионов водорода в растворе и его рН.

Решение: Удельная 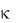и молярная 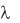электрические проводимости связаны между собой соотношением = 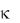1000/С, где С – концентрация в моль/л; 1000 — пересчетный коэффициент из л в см3.

Рассчитываем :

0,476 1000 = = 2,72 Ом 1см2моль 1

0,175

Степень ионизации вычисляется с помощью уравнения: = /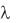, где

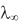– мольная (эквивалентная) проводимость при бесконечном разведении,

70