Основной текст

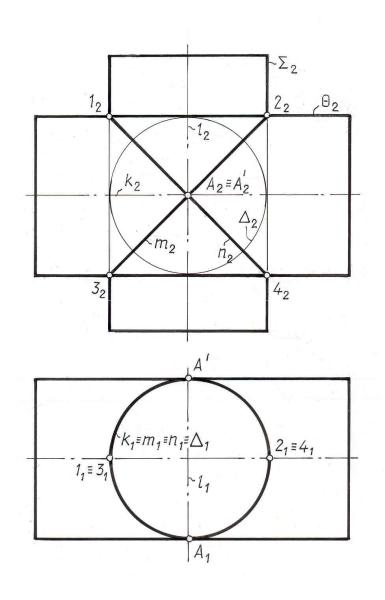
У

Т

Н

Б

й

и

р

о

т

и

з

Рис. 8. 5.

о

Рассм трим приложение выше сказанного к построению линий пересе-

п

чения двух

рямых круговых конусов: вертикального и горизонтального Г.

Р

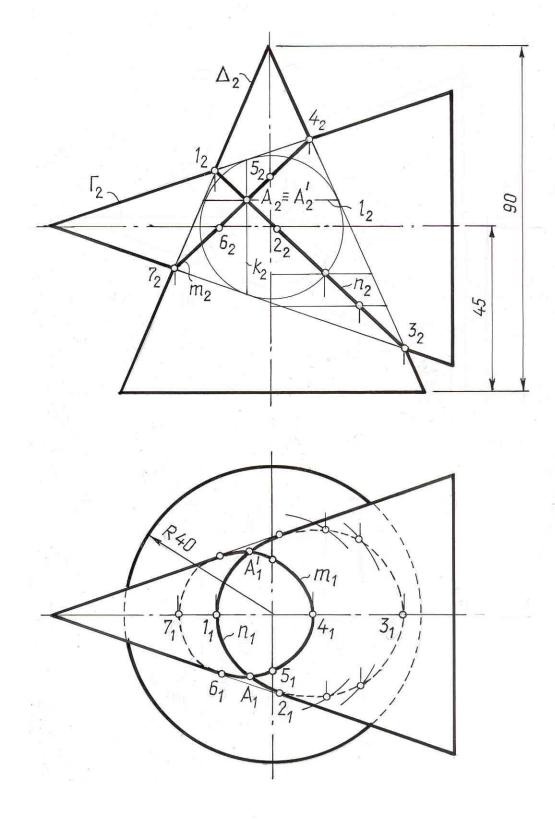
Задача 4. Найти линию пересечению двух прямых круговых конусов

Дано:

и Г – конусы

(рис. 8. 6).

е

∩ Г =?

Решение: ∩ Г = m, n –

две плоские кривые.

У

Т

Н

Б

й

и

р

о

т

и

з

о

п

е

Р

Рис. 8.6

m2 и n2

, которые и в этом случае будут эллипсами. Если задача решена с дос-

таточной точностью, то m и

n обязательно пересекутся в точках соприкос-

новения

A и A'.

В других случаях, отвечающих условиям теоремы Монжа, при изменении

относительных размеров и взаимного положения поверхностей вращения в

пространстве линии их пересечения могут принимать форму гипербол или па-

рабол.

Следует отметить, что пересечение по теореме Монжа является погранич-

ным случаем в очертании линий пересечения поверхностей вращения.

У

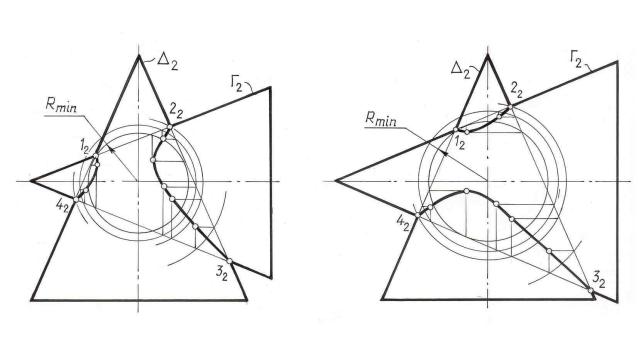
Если в последней задаче изменить относительные размеры конусов так

чтобы сфера минимального радиуса (Rmin ) вписывалась бы в вертикальный ко-

нус , а горизонтальный пересекала, то линии их пересечения распадутсяТна

две пространственные кривые

m и n , полностью пересекающие образующие

горизонтального конуса Γ (рис. 8.7). В этом случае горизонтальный конус про-

тыкает вертикальный.

Н

При изменении параметров конусов таким образом, чтобы сфера мини-

Б

мального радиуса Rmin вписывалась в горизонтальный конус и пересекала верти-

кальный (рис. 8.8), характер пересечен я меняется. Теперь уже вертикальный ко-

нус протыкает горизонтальный.

й

и

р

о

т

и

з

о

п

е

Р

Рис. 8.7

Рис. 8.8