
РТЦС-методичка
.pdf
--1--
Задание на контрольную работу и общие указания к ее выполнению
Контрольная работа включает в себя 10 расчетных задач, относящихся к разным (десяти) разделам программы преподавания дисциплины «Радиотехнические цепи и сигналы».
Контрольная работа выполняется по вариантам. Номер (N) своего варианта студент выясняет лично у преподавателя на установочных занятиях. Номер варианта не имеет никакого отношения к цифрам в номере зачетной книжки.
После выполнения расчетной части контрольной работы студент обязан оформить ее в виде подробного отчета, сдать преподавателю на проверку (в часы плановых консультаций) и при необходимости защитить работу.
Оформление отчета производится в соответствии с требованиями стандарта.
Раздел 1. Спектральный анализ периодических радиосигналов
1.1. Краткое теоретическое введение
Гармоническим рядом Фурье называют разложение в ряд [1,
с. 22; 2, с. 42; 3, с. 39]
|
|
cos(n t ) |
(1.1.1) |
s(t) = s_ S |
n |
||
|
n |
|
n 1
периодических сигналов и сигналов, заданным на конечном интервале времени. Его параметры и коэффициенты определяются в соответствии с соотношениями
|
|
|
|
|
|
|
|
|
1 |
t |
0 |
Т |
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
s_ = |
|
|
s(t) dt |
|
|
(1.1.2) |
||||||
|
|
|
|
|
|
|
Тп |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S |
n |
= |
a |
2 |
b |
2 |
, |
Ψ |
n |
= arctg( b |
/ a ), |
Ω = 2π/Т |
п |
, (1.1.3) |
|||||
|
|
|
n |
|
n |
|
|
|
|
|
|
|
n |
n |
|
|
|||
--2--
где Тп - интервал определения сигнала во времени или период сигнала; t0 - начало интервала определения сигнала конечной длительности или произвольный момент для периодического сигнала;
|
2 |
|
t0 Тп |
2 |
|
t0 Тп |
|||
an = |
|
|
s(t) cos(n t)dt , bn = |
|
|
s(t) sin(n t)dt . |
|||
|
|
||||||||
|
Тп |
t0 |
|
Тп |
t0 |
|
|||
Совокупность коэффициентов разложения s_ и Sn (n≥1) принято называть гармоническим спектром Фурье сигнала s(t), а слагаемые ряда (1.1.1) - гармоническими спектральными составляющими.
Комплексным рядом Фурье называют представление сигнала в виде ряда
|
|
e j n t |
, |
(1.1.4) |
s(t) = c |
n |
n -
где коэффициенты cn , называемые в совокупности комплекс-
ным (двухсторонним) спектром Фурье сигнала s(t) , определяются соотношением [1, с. 21; 2, с. 44; 3, с. 42]
c |
|
|
1 |
t |
0 |
Т |
п |
s(t) e jn tdt. |
|
||
n |
= |
|
|
(1.1.5) |
|||||||
|
|
|
|||||||||
|
|
Т |
п |
|
|
t |
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
||
Спектральными составляющими, соответствующими этой форме записи ряда Фурье, являются комплексные функции
cn e jn t . Поскольку величины cn несут в себе информацию
сразу как об амплитуде, так и фазе составляющих, при графическом представлении обычно строят отдельно спектр амплитуд сигнала s(t), определяемый модулями коэффициентов cn , и его
спектр фаз, определяемый аргументами величин cn .
Между гармоническим (односторонним) и комплексным (двухсторонним) спектром сигнала s(t) существует однозначная связь
|
|
|
|
--3-- |
|
|
|cn | = s_ (n = 0); |
|cn | |
= 0.5 · S|n| (n ≠ 0); |
|
|||
|
|
|
|
|
при n 0 |
|
arg(c |
|
) = |
|
n |
|
(1.1.6) |
n |
|
при n 0 |
||||
|
|
|
|
|
||
|
|
|
|
|n| |
|
|
1.2. Типовые задачи
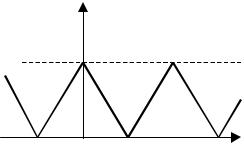
Задача 1. Рассчитать гармонический и комплексный спектры Фурье сигнала, представленного на рис. 1.
|
|
s(t), В |
|
|
S0 |
|
|
-Тп/2 |
0 |
Тп/2 |
t, с |
|
|
Рис. 1 |
|
Решение
а) Поскольку гармонический и комплексный спектры сигнала жестко связаны между собой, то не имеет смысла рассчитывать их по отдельности друг от друга; достаточно получить тот из них, для которого требуется меньше расчетов, а второй определять учитывая соотношения (1.1.6). Поскольку, расчет комплексного спектра оказывается обычно компактнее, за основу дальнейшего анализа принимаем соотношение (1.1.4).
б) Так как соотношение (1.1.4) требует знания аналитического выражения сигнала на произвольном временном интервале длительностью в один период, то будем работать с интервалом
от -Тп/2 до +Тп/2. Как при t > 0, так и при t < 0 анализируемый сигнал изменяется линейно, причем s(0) = S0, поэтому аналити-

--4--
ческое выражение будем искать в виде s(t) = S0 + k·t. Взяв в качестве второй контрольной точки нулевые значения для t = -
Тп/2 до и t = +Тп/2, получаем окончательно |
|
|
|||||||
|
S0 |
1 |
2 t Тп |
, |
при 0 t Тп / 2 |
|
|||
s(t) = |
S |
1 |
2 t Т |
п |
, |
при -Т |
п |
/ 2 t 0 |
(1.2.1) |
|
0 |
|
|
|
|
|
|
||
в) Теперь для расчета коэффициентов cn комплексного ряда Фурье достаточно подставить (1.2.1) в (1.1.4), однако вследст-
вие различного поведения сигнала на интервалах -Тп/2 ≤ t ≤ 0 и
0 ≤ t ≤ +Тп/2 при этом придется по отдельности рассчитывать два соответствующих интеграла. Вместе с тем, сигнал s(t) определяется четной математической функцией, а комплексная экспонента, на которую он умножается в (1.1.4) имеет четную действительную и нечетную мнимую части, поэтому независимо от конкретной формы сигнала интегралы по области t < 0 и t > 0 будут обладать одинаковыми действительными и противоположными по знаку мнимыми частями. По указанной причине выгодно воспользоваться следующей модификацией формулы (1.1.4)
|
|
|
|
|
2 |
|
Тп /2 |
|
|
|
|
j n t |
|
|
|
|||||
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
= |
|
|
Re |
s(t) e |
|
|
dt |
= |
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
n |
|
Т |
п |
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 S0 |
|
Тп / 2 |
j n t |
|
2 |
|
|
Тп /2 |
|
jn t |
|
||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Re |
|
e |
|
|
dt |
|
|
|
|
t e |
|
|
dt |
|||||
Т |
|
|
|
|
Т |
|
|
|
|
|||||||||||
|
п |
|
|
|
0 |
|
|
|
|
|
п |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Применяя для последнего слагаемого интегрирование по частям
u = t, du = dt; |
dv = e jn tdt , v = e jn tdt |
=e j n t |
j n , |
||||||||
|
|
|
2 S |
|
j n Тп / 2 |
1 |
|
|
|||
|
|
|
e |
|
|
|
|||||
получаем c |
n |
= |
|
0 |
Re |
|
|
|
- |
|
|
Т |
|
|
j n |
|
|
|
|||||
|
|
п |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||

--5--
2 |
|
|
Тп |
|
e |
j n Т |
п / 2 |
1 |
Т |
п / 2 |
j n t |
|
|
|
|||
|
|
|
|
|
|
e |
|
|
= |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
||
Т |
|
2 |
|
j n |
|
|
|
||||||||||
|
п |
|
|
|
|
j n 0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j n Т /2 |
|
|
|
|
|
|
|
|
|
|
|||
|
2 S |
1 |
|
|
|
2 |
|
e |
п |
|
|
|
|
|
4 S |
|
|
j n Т /2 |
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||
= |
0 |
Re |
|
|
|
|
|
|
|
|
|
|
|
= |
0 |
|
|
Re 1 e |
п |
= |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|||||||||||
|
Т |
j n Т |
|
|
|
n |
|
|
|
|
n Т |
|
|
|
|
|||||||||
|
п |
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|||
|
= |
|
S0 |
|
|
|
1 cos n Тп / 2 = |
S0 |
|
1 cos n |
|
|
||||||||||||
|
n Тп |
2 2 |
|
n 2 |
|
|
|
|||||||||||||||||
где последнее |
равенство основано |
на (1.1.3), откуда |
следует |
|||||||||||||||||||||
Ω·Тп/2 = π. Этот результат можно дополнительно упростить, если рассмотреть в отдельности случаи, когда n-четное и в квадратных скобках получаем нулевое значение, и когда n- нечетное и [1 - cos(nπ)] = 2. Обратите внимание, что n = 0 представляет собой особый случай, поскольку при этом не только числитель, но и знаменатель оказывается нулевым, поэтому постоянную составляющую следует рассчитывать отдельно. Воспользовавшись (1.1.2), легко убедиться, что s_ = S0/2. Таким образом,
S0 2, при n 0
cn = |
|
|
0, |
при n -четных |
(1.2.2) |
|
|
2 S |
n 2, |
при n -нечетных |
|
|
|
0 |
|
|
|
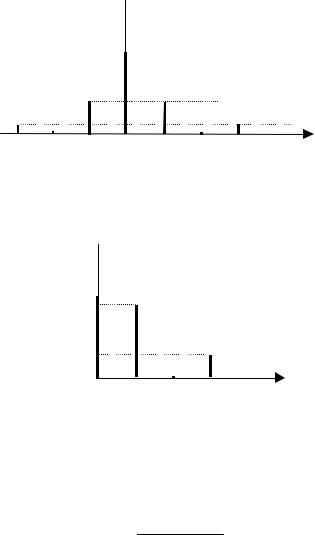
г) Соответствующий (1.2.2) спектр амплитуд сигнала s(t) показан на рис.2. Спектр фаз строить в данном случае не имеет смысла, так как все коэффициенты оказались чисто действительными (вследствие четности s(t)), а значит начальные фазы всех составляющих являются нулевыми. Гармонический спектр, полученный из комплексного на основе соотношений (1.1.6), приведен на рис.3. Обратите внимание, что постоянная составляющая остается неизменной, а удваиваются лишь амплитуды гармоник положительных частот.
--6--
 |cn|, В
|cn|, В
S0/2
2S0/π2
2S0/9π2
-3/Тп -1/Тп 0 1/Тп |
3/Тп f, Гц |
Рис. 2. Комплексный спектр сигнала
 Sn, В
Sn, В
S0/2
4S0/π2
4S0/9π2
0 1/Тп |
3/Тп f, Гц |
Рис. 3. Гармонический спектр сигнала
Задача 2. Рассчитать комплексный спектр амплитуд и спектр фаз Фурье сигнала
|
8 tg 0 t |
||
s(t) = |
1 tg2 |
0 |
t , В. |
|
|
|
|
Решение Хотя по условию задачи требуется рассчитать конкретно
комплексный спектр сигнала, пытаться непосредственно применить стандартную формулу (1.1.4) к заданному сигналу s(t) не
--7--
следует. Подобный формальный подход порождает весьма громоздкий интеграл, который может многих (на первый взгляд) поставить в тупик. В данном случае крайне важно вспомнить, что сущность спектрального анализа заключается в представлении сигналов в виде суммы заданного вида слагаемых. Соотношение (1.1.4) представляет лишь один из возможных способов получения такой суммы, гарантирующий минимальную среднеквадратическую погрешность. Однако любой другой способ, который обеспечивает минимум среднеквадратической погрешности при переходе от сигнала s(t) к его представлению в виде ряда (1.1.1), также является допустимым. В связи с этим, для приведения сигнала s(t) к виду (1.1.1) можно использовать любое тождественное математическое преобразование, а для разбираемого в данной задаче сигнала такое преобразование является очевидным:
|
8 tg 0 t |
|
8 tg 0 t |
||||||
s(t) = |
|
|
|
|
= |
|
|
|
= |
1 tg |
2 |
0 |
t |
1/ cos2 |
0 |
t |
|||
|
|
|
|
|
|
|
|
||
|
|
= 8·sin(ω0·t)·cos(ω0·t) |
= 4·sin(2·ω0·t), В (1.2.3) |
||||||
Если бы в задаче требовалось построить гармонический спектр сигнала, то после выполненных преобразований ее можно было бы считать практически решенной. Необходимо лишь учесть, что хотя с позиций математики последнее полученное выражение является наиболее компактным, для построения гармонического спектра его все же необходимо преобразовать к виду s(t) = 4·cos(2·ω0·t - π/2), В. Ведь именно суммой косинусо-
ид определяется гармонический ряд Фурье (1.1.1). Использование же (1.2.3) может привести к некорректному представлению о фазовом спектре сигнала.
Для построения требуемого по условию комплексного спектра сигнала применим формулу Эйлера, заменяя cos(·) суммой двух комплексных экспонент
s(t) = 4·cos(2·ω0·t - π/2) = |
2 e |
j 2 0 t /2 |
2 e |
-j 2 0 |
t /2 |
, В |
|
|
|
--8--
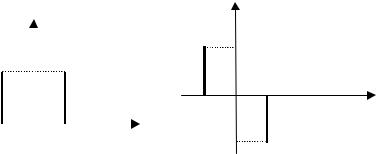
Полученное аналитическое представление сигнала, очевидно, соответствует спектрам амплитуд и фаз, показанным на рис. 4 и 5.
|
|
|сn|, В |
arg(сn), рад |
||
2 |
+π/2 |
||||
|
|
||||
|
|
|
|||
|
|
|
|
0 +2·ω0 ω, рад/с |
|
|
|
|
|
-2·ω0 |
|
|
|
|
|
|
|
-2·ω0 0 +2·ω0 ω, рад/с |
-π/2 |
||||
|
Рис. 1. Спектр амплитуд |
Рис. 2. Спектр фаз сигнала |
|||
Для более полного усвоения учебного материала разберите также решения задач 2.7, 2.9-2.11, приведенные в задачнике [5,
с. 12-15].
Задача контрольной работы (№1):
По заданному аналитическому выражению колебания
рассчитать и построить гармонический (односторонний) и комплексный (двухсторонний) спектр сигнала;
для каждого типа спектра указать общее количество и час- тоты всех спектральных составляющих (включая постоянную составляющую);
написать аналитические выражения спектральных составляющих наибольших частот для гармонического и для комплексного спектра;
для следующих токов i(t), измеряемых в миллиамперах,
Вариант |
Аналитическое выражение колебания |
|
|
1 |
300 · cos(2 103t) · (1 + cos(4 103t)) |
|
|
2 |
80 · sin(2 103t) · cos(4 103t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
--9-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 I0 t / Тп, |
|
при 0 t Тп / 2 |
|
|
|
|||||||||||||||||||||||
|
-2 I0 |
|
t / Тп, |
|
при -Тп / |
2 t 0 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
4 |
|
|
-I |
0 |
|
, |
|
при 0 t Т |
п |
/ 2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
I0, |
|
при -Тп / 2 t 0 |
|
|
|
|
|
|
|||||||||||||||||||
|
I0 1 4 t |
|
Тп |
, |
при |
|
0 t Тп / 2 |
||||||||||||||||||||||
5 |
|
I |
0 |
1 4 t |
|
Т |
п |
, |
при |
|
|
-Т |
п |
/ 2 t 0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6 |
|
|
|
0, |
|
|
|
при 0 t Тп /2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
I0, |
|
при -Тп /2 t 0 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
7 |
I0 e |
|
10 t Тп |
|
, |
при -Тп/2 ≤ t ≤ Тп/2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
8 |
|
I |
0 |
, |
|
при 0 t Т |
п |
/2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0, |
|
|
|
при -Тп /2 t 0 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
t Т |
|
|
|
|
|
|
|
|
|
|
Т |
п |
|
|
Т |
п |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
9 |
I |
0 |
e |
|
|
п |
|
|
1 , |
при - |
|
|
|
≤ t ≤ |
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
10 |
|
I |
0 |
|
, |
|
при 0 t Т |
п |
|
/ 2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
-I0, |
|
при -Тп / 2 t 0 |
|
|
|
|
|
|
|
||||||||||||||||||
Тп следует считать произвольной по величине константой.
--10--
Раздел 2. Спектральная плотность непериодических сигналов
2.1. Краткое теоретическое введение
Спектр непериодических видеоимпульсов состоит из бесконечного числа спектральных составляющих бесконечно малой амплитуды лежащих на бесконечно малом расстоянии друг от друга, то есть является сплошным. Поскольку оперировать с бесконечно малыми величинами на практике неудобно, частотные свойства таких сигналов принято характеризовать их комплексной спектральной плотностью, получаемой из временного описания при помощи прямого преобразования Фурье [1, с. 28; 2, с. 50; 3, с. 45]
|
( ) = |
|
|
-j t |
dt . |
(2.1.1) |
|
|
s(t) e |
||||||
Gs |
|
Обратное преобразование (из частотной области во временную) можно осуществить, используя обратное преобразование Фурье
s(t) = |
|
|
|
j t |
d . |
(2.1.2) |
|
|
( ) e |
||||||
Gs |
|
Модуль комплексной спектральной плотности имеет размерность В/Гц (для напряжений) и А/Гц (для токов) и называется спектральной плотностью амплитуд сигнала; аргумент спектральной плотности arg(Gs( ) ) измеряется в радианах и назы-
вается спектром фаз сигнала s(t).
Из сопоставления определений (2.1.2) и (1.1.5) видно, что между комплексной спектральной плотностью одиночного видеоимпульса и комплексным спектром Фурье периодического повторения этих импульсов существует простая и четкая взаимосвязь
c |
1 |
|
n , Ω = 2π/Тп |
|
||
= |
Т |
|
G |
(2.1.3) |
||
n |
|
п |
s |
|
|
|
|
|
|
|
|
|
|
