
РТЦС-методичка
.pdf--51--
сигнал s1(k) реального фильтра в (7.1.2) можно ограничиться лишь неотрицательными индексами суммирования.
Комплексный коэффициент передачи дискретного фильтра представляет собой комплексное число, модуль которого определяет во сколько раз после прохождения через фильтр увеличивается амплитуда гармонического колебания, а аргумент - какое приращение получает при этом начальная фаза колебания. Можно показать, что с импульсной характеристикой и масштабными коэффициентами ветвей фильтра его комплексный коэффициент передачи связан соотношением
|
|
|
|
|
|
R |
|
e j rT |
|
|
|
|
|
j rT |
|
a |
r |
||
|
|
|
r 0 |
|
|
||||
|
|
g(r) e |
|
|
|
|
|||
K |
T |
( ) |
|
|
|
|
|
. (7.1.3) |
|
|
M |
|
|
||||||
|
|
r |
|
|
|
e j mT |
|||
|
|
|
|
|
1 b |
||||
m
m 1
7.2. Т и п о в ы е з а д а ч и
Задача 1. Предложить структурную схему фильтра, импульсная характеристика которого определяется выражением
1, при r -четном g(r) =
0, при r -нечетном
Построить амплитудно-частотную характеристику этого фильтра для случая, когда один такт задержки сигнала составляет
T = 0,2 мкс.
Решение
а) Структурная схема дискретного фильтра однозначно определяется коэффициентами передачи его ветвей, которые в свою очередь в явной форме входят в его комплексной коэффициент передачи. Воспользовавшись (7.1.3) и правилом суммирования бесконечной геометрической прогрессии, запишем
|
|
|
|
j rT |
|
|
j 2kT |
|
|
( ) |
g(r) e |
|
g(2k) e |
= |
|||
K |
T |
|
|
|||||
|
|
r |
|
r 2k |
k |
|
|
|
|
|
|
|
|
|
--52--
|
j 2kT = 1 |
1-e j 2T . |
= e |
||
k |
|
|
Сопоставляя полученное выражение с правой половиной (7.1.3)
нетрудно заметить, что a0 = 1, ar = 0 (при r ≥ 1), b1 = 0, b2 = 1,
bm = 0 (при m ≥ 2). Таким образом, задаваемый условием задачи фильтр может быть реализован при помощи структурной схемы, показанной на рис. 26.
s1(k) |
+ |
s2(k) |
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
Рис. 26. Рекомендуемая для задачи 1 структурная схема фильтра б) Амплитудно-частотная характеристика дискретного фильтра, как и в случае анализа фильтра аналогового, представляет собой модуль величины K , но отличается от характеристик аналоговых цепей периодичностью по частоте
|
|
|
|
1 |
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
||||||
KT |
( ) |
|
|
|
|
|
|
|
|
|
|
|
2 1-cos(2 T) |
|
2 sin( T ) |
||||||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
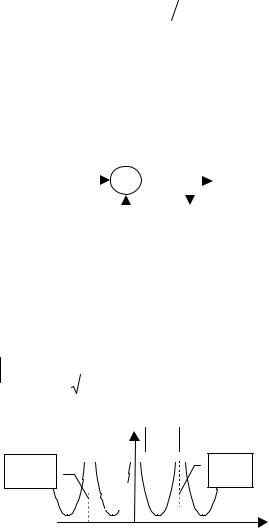
Соответствующий этомувыражению график показан на рис. 27.
|
|
|
K |
-1/2T |
1/2T |
0,5 |
|
-2,5 0 |
2,5 f, МГц |
Рис. 27. АЧХ дискретного фильтра из задачи 1
Задача 2. Определить импульсную характеристику фильтра, показанного на рис. 28, и рассчитать его реакцию на сигнал x(k) = { 2; -3; 2 }.
|
|
|
--53-- |
|
|
|
|
s1(k) |
2 |
|
+ |
s2(k) |
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
T |
|
|
|
T |
|||
|
|
-0,5 |
|
|
0,5 |
|
|
|
|
|
|
|
|
||
|
|
|
|||||
|
|
|
|
|
|
||
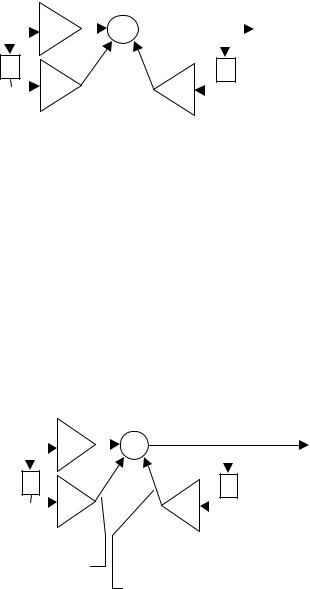
Рис. 28. Структурная схема анализируемого фильтра
Решение
а) Простейшим способом оценки импульсной характеристики дискретного фильтра является расчет его реакции на единичный воздействующий импульс, выполняемый непосредственно по структурной схеме фильтра (правда при таком подходе достаточно сложно "угадать" общее аналитическое выражение импульсной характеристики). Для этого достаточно выписать последовательно значения отсчетов, наблюдаемых на разных тактах на входе и выходе фильтра, а также на выходах всех устройств задержки. Структурная схема фильтра с соответствующими пометками (наблюдаемыми в разных узлах дискретными последовательностями отсчетов) приведена на рис. 29.
s1(k) ={ 1; 0; 0…} |
2 |
|
+ |
s2(k)={ 2; 0,5; 0,25…} |
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
T |
-0,5 |
|
|
0,5 |
T |
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
s1+T(k)={ 0; 1; 0…}
s2+T(k) ={ 0; 2; 0,5…}
sa1(k) ={ 0; -0,5; 0…}
sb1(k)={0; 1; 0,25; 0,125}
Рис. 29. Структурная схема фильтра с последовательностями наблюдаемых отсчетов
--54--
Поскольку начиная со второго такта выходной сигнал определяется уже не входным воздействием, но лишь отсчетами, передаваемыми на сумматор схемы через ветвь b1, то, очевидно, каждое последующее выходное значение будет просто вдвое меньше предыдущего. Получаемый в результате подобного потактного анализа сигнал s2(k) и является, очевидно, импульсной характеристикой фильтра
2, приr 0 g( r ) = s2( r ) = -r
2 , приr 1
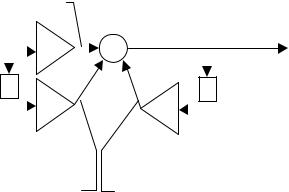
б) Реакцию фильтра на входной сигнал x(k) можно, очевидно, получить аналогичным образом, т. е. путем потактного прослеживания сигналов в различных точках структурной схемы фильтра. В связи с большей протяженностью входного воздействия необходимо лишь выполнять подобный анализ для большего числа тактов (см. рис. 30).
xa0(k)={4; -6; 4; 0…} |
|
y(k)={4; -5; 3; 0,5…} |
||||||
|
|
|
|
2 |
|
|||
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
||
x(k) ={ 2; -3; |
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
||||
2; 0; 0…} T |
|
|
T |
|||||
|
|
|
|
-0,5 |
0,5 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
y+T(k) ={ 0; 4; -5; |
||
x+T(k)={0; 2; -3; 2; 0…} |
|
|
|
3; 0,5…} |
||||
xa1(k)={0;-1;1,5;-1;0…} yb1(k)={0;2;-2,5;1,5;0,25…}
Рис. 30. Структурная схема фильтра с последовательностями отсчетов, наблюдаемых при воздействии x(k)
Таким образом, откликом на последовательность отсчетов x(k) служит дискретный сигнал y(k) = { 4; -5; 3; 0,5; 0,25…}.
--55--
Для более полного усвоения учебного материала разберите также решения задач 12.31-12.34, приведенные в задачнике [5,
с. 192-195].
Задача контрольной работы (№7):
По заданной структурной схеме дискретного фильтраопределить его импульсную характеристику;
рассчитать и построить отклик этого фильтра на заданный входной сигнал.
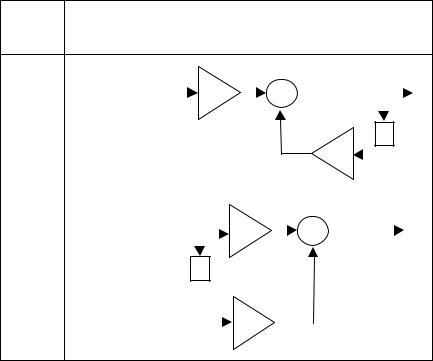
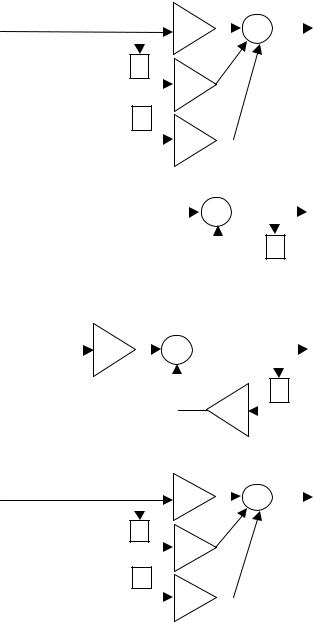
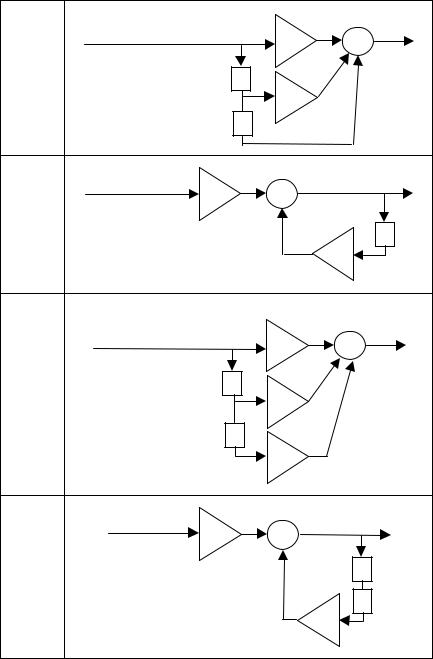
Схемы подлежащих анализу фильтров и воздействующие на них сигналы приведены в таблице ниже
Вари- |
Схема фильтра, входной сигнал фильтра |
ант |
|
|
|
|
2 |
|
|
|
|
+ |
|
|
|
s2(k) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
s1(k) = |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
T |
|
|||||||||||||
|
={ 0; 2; 0; -1; 0; 0… } |
|
|
|
|
|
|
|
||||||||||||
|
|
0,5 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
s1(k) = 4 · 2-k |
|
|
|
|
|
s2(k) |
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
+ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
-0,5 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
--56--
|
s1(k) = |
|
|
|
|
|
|
|
|
|
|
|
s2(k) |
||||||||||
|
|
|
={ 1; 0; 3; 0; 0… } |
-0,5 |
|
|
|
+ |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
T |
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
1,5 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
s2(k) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
s1(k) = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
T |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
= { 2; 0; -1; 0; -1; 0; 0… } |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3 |
|
|
|
|
+ |
|
|
|
|
|
s2(k) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5 |
|
s1(k) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
T |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
= { 0; 2; 2; 0; 0… } |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
-1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
s1(k) = |
|
|
|
|
|
|
|
|
|
|
|
s2(k) |
||||||||||
|
|
|
={ 1; 2; 4; 0; 0… } |
2 |
|
|
|
|
+ |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6 |
|
|
|
T |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
T |
-1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
--57-- |
|
|
|
|
2 |
s2(k) |
|
s1(k) = |
+ |
|
|
|
|
|
7 |
={ -1; 3; 0; 0… } T |
-2 |
|
|
|
|
|
|
T |
|
|
|
3 |
+ |
s2(k) |
|
|
||
8 |
s1(k) = |
|
T |
= { 2; 0; -0,5; 0; 0… } |
|
||
|
|
||
|
|
|
-0,5 |
|
s1(k) = |
|
s2(k) |
|
={ 0; 1; 1; 0; 0… } |
6 |
|
|
+ |
||
9 |
T |
-3 |
|
|
|
||
|
T |
2 |
|
|
|
|
|
|
-1 |
+ |
s2(k) |
|
|
||
|
s1(k) = |
|
T |
10 |
= { 3; 0; 3; 0; 0… } |
|
|
|
|
||
|
|
|
T |
|
|
|
-1 |

--58--
Раздел 8. Z-преобразование и его применение для анализа дискретных и цифровых фильтров.
8.1. К р а т к о е т е о р е т и ч е с к о е в в е д е н и е
Прямым Z-преобразованием дискретного сигнала s(k) называется комплексная функция комплексного аргумента z, рассчитываемая по формуле
S(z) |
|
-k . |
|
s(k) z |
(8.1.1) |
k 0
Для восстановления по Z-образу исходной последовательности отсчетов применяют обратное Z-преобразование
s(k) |
1 |
|
|
|
S(z) zk-1 dz. |
(8.1.2) |
||
2 j |
||||||||
|
|
z |
1 |
|
|
|||
Следует отметить, что непосредственное использование выражения (8.1.2) редко приводит к удобным математическим выражениям, однако подобное интегрирование по замкнутому контуру значительно облегчается использованием теоремы о вычетах, которая утверждает
1 где resi mi -1 !
s(k) = |
res |
i |
|
|
(8.1.3) |
|||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
d(mi 1) |
(z z |
|
)mi S(z) zk 1 |
(8.1.3') |
|||
|
(m 1) |
i |
||||||
z zi |
(dz) |
|
|
|
|
|||
|
i |
|
|
|
|
|
||
- вычет подынтегральной функции в точке zi; zi - полюс функ-
ции S(z), т.е. значение аргумента z, обращающее эту функцию
в бесконечность, mi - кратность полюса zi.
Применение Z-преобразования при анализе дискретных и цифровых фильтров позволяет преобразовать разностное уравнение (7.1.1) в алгебраическое уравнение, связывающее Z-образы сигналов на входе и выходе фильтра
|
|
|
(8.1.4) |
S2 |
(z) S1 |
(z) H(z), |
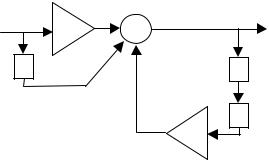
--59--
где S1(z) и S2(z) - результаты Z-преобразования соответст-
венно входного и выходного сигналов, а H(z) - системная функция фильтра, определяемая соотношением
|
|
|
|
|
|
R |
|
z-r |
|
|
|
|
|
|
|
-r |
|
|
a |
r |
|
|
|
||
|
|
|
r 0 |
|
|
|
|
|
||||
g(r) z |
|
|
|
|
|
|
|
|
||||
H(z) = |
|
= |
|
|
|
|
|
|
. |
(8.1.5) |
||
|
|
M |
|
|
|
|
||||||
|
r 0 |
|
|
|
|
|
|
z |
-m |
|
||
|
|
|
|
1- b |
m |
|
||||||
|
|
|
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Системная функция |
|
|
дискретного |
фильтра является |
||||||||
H(z) |
||||||||||||
аналогом его комплексного коэффициента передачи, рассчитанным (в отличие от последнего) на работу в комплексной плоскости z и более удобным для анализа дискретных сигналов вследствие простоты применения теоремы о вычетах (8.1.3) для нахождения реакции фильтра на заданное воздействие.
8.2. Т и п о в ы е з а д а ч и
Задача 1. Определить общее аналитическое выражение импульсной характеристики фильтра, структурная схема которого представлена на рис. 31.
s1(k) 2 |
+ |
s2(k) |
T |
|
T |
|
|
T |
|
|
0,5 |
Рис. 31. Структурная схема дискретного фильтра к задаче 1
Решение

--60--
а) Из структурной схемы фильтра следует, что коэффици-
енты передачи ветвей фильтра равны a0 = 2, a1 = 1, ar = 0 (r≥2),
b1 = 0, b2 = 0,5, bm = 0 (m≥3). Подставляя эти коэффициенты в правую половину соотношения (8.1.5) получим системную функцию данного фильтра
|
2 z |
-1 |
|
H(z) = |
|
|
. |
|
|
||
|
1-0,5z-2 |
||
б) Поскольку в соответствии с левой половиной соотношения (8.1.5) системная функция является Z-преобразованием его импульсной характеристики, то самуимпульсную характеристику можно рассчитать по найденной H(z)при помощи обратного Z-преобразования. Для нахождения полюсов системной функции и числитель, и знаменатель H(z) умножим на z в такой степени, чтобы в знаменателе не осталось отрицательных сте-
|
2 |
|
|
|
|||||
пеней z (в данном случае это z |
). Тогда H(z) приобретет вид |
||||||||
|
2 z 2 z 1 |
|
|
2 z2 z |
|||||
H(z) = |
|
= |
|
. |
|||||
|
|
||||||||
|
z 2 -0,5 |
|
(z- |
0,5) |
(z |
0,5) |
|
|
|
Из последней формы записи очевидно, что H(z) имеет два по-
люса z1 = 
 0,5 и z2 =
0,5 и z2 = 
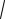 0,5 кратности m = 1 (такие полю-
0,5 кратности m = 1 (такие полю-
са называют еще простыми). В результате формула (8.1.3'), определяющая значение вычета, упрощается к виду
res |
i |
lim |
(z z |
i |
) S(z) zk 1 |
|
(8.2.1) |
|
z z |
i |
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Таким образом, импульсная характеристика анализируемого фильтра может быть рассчитана как сумма двух вычетов
g(r) = lim (z |
|
|
r 1 |
+ |
lim (z |
|
|
r 1 |
= |
||
|
|
||||||||||
0,5) H(z) z |
|
0,5) H(z) z |
|
||||||||
z 0,5 |
|
|
|
|
z |
0,5 |
|
|
|
|
|
