
РТЦС-методичка
.pdf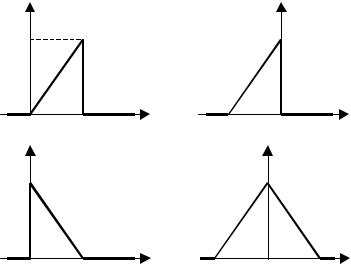
--11--
Полезно помнить, что преобразование Фурье является родственным преобразованию Лапласа [1, с.55-57], поэтому вместо (2.1.1), (2.1.2) нередко выгоднее использовать приводимые во многих математических справочниках таблицы преобразований Лапласа.
При определении спектральных характеристик также очень полезно использовать теоремы о спектрах, которые в наиболее компактном виде приведены в [2, с. 52-53].
2.2. Типовые задачи
Задача 1. Рассчитать комплексную спектральную плотность видеоимпульсов, представленных на рис. 6.
S0 |
s1(t), В |
|
s2(t), В |
S0 |
|
|
|
|
|
|
|
||
а) |
|
|
б) |
|
|
|
0 |
Т |
t, с |
0 |
|
Т |
t, с |
S0 |
s3(t), В |
|
|
S0 |
s4(t), В |
|
|
|
|
|
|
|
|
в) |
|
|
г) |
|
|
|
0 |
Т |
t, с |
-T |
0 |
|
Т t,с |
Решение |
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
а) Поскольку сигнал изменяется на интервале определения линейно, то его аналитическое выражение имеет смысл искать в виде s1(t) = kt. Используя в качестве контрольной точки s1(T) =
--12--
= S0, нетрудно убедиться, что приведенному на рис. 6а сигналу соответствует функция
s1(t) = |
|
S t / T, |
0 t T |
|
0 |
(2.2.1) |
|
|
|
0, при прочих t |
|
Подставляя (2.2.1) в определение (2.1.1) и интегрируя по частям (с
подстановками u=t; dv = e j t dt), получим
|
|
S |
|
j t |
|
j t |
|
Т |
j Т |
S e j Т |
1 |
|||
|
|
|
||||||||||||
|
0 |
t e |
|
e |
|
|
|
e |
0 |
|
|
|||
G1 |
( ) = |
|
|
|
|
|
|
|
= S0 |
|
|
|
|
. (2.2.2) |
|
|
2 |
|
|
2 |
|
||||||||
|
|
Т |
|
j |
|
|
|
|
0 |
j |
Т |
|
|
|
|
|
|
|
|
|
|
||||||||
б) Расчет спектральных характеристик сигнала s2(t), представленного на рис. 6б, можно, конечно, выполнить аналогично проведенному выше, однако если вспомнить о существовании теоремы о запаздывании сигнала [2, с.52], то можно обойтись без расчета интеграла (2.1.1). Действительно, сигнал s2(t) опережает сигнал s1(t) по времени на интервал Т, поэтому используя (2.2.2) и отрицательную по знаку задержку
tз = -T, получаем |
|
|
|
|
|
|
|
1-e j Т |
|
|
||
|
|
|
j t |
з |
|
S |
|
S |
|
|
||
|
|
|
0 |
|
0 |
|
|
|
||||
G2 |
( ) = G1 |
( ) e |
|
|
= |
|
|
|
|
|
. |
(2.2.3) |
|
|
j |
|
Т 2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
в) Аналогично, вместо непосредственного применения (2.1.1) к расчету спектральной плотности сигнала s3(t), показанного на рис. 6в, целесообразно учесть, что s3(t) получается из s2(t) путем инверсии аргумента t. Поэтому, применяя к спектральной плотности G2 ( ) операцию комплексного сопряжения, получаем
|
|
* |
|
S |
0 |
|
S 1-e j Т |
|
|
||
|
|
|
|
0 |
|
|
|
||||
G3 |
( ) |
= G2 |
( ) = |
|
|
|
|
|
. |
(2.2.4) |
|
j |
Т 2 |
||||||||||
|
|
|
|
|
|
|
|||||
г) Наконец, |
|
|
( ), соответствующей сигналу, по- |
||||||||
для расчета G4 |
|||||||||||
казанному на рис. 6г, следует просуммировать спектральные плотности G2( ) и G3( ), или, используя их комплексную со-
пряженность, воспользоваться соотношением
--13--
|
|
|
2 S0 |
|
|
G4 |
( ) = 2 Re G2 |
( ) = |
|
1-cos( Т) . (2.2.5) |
|
Т 2 |
|||||
|
|
|
|
Итак, знание теорем о спектрах позволило оперативно и просто получить целый набор спектральных плотностей сигналов без выполнения операции интегрирования.
Примечание:
На основе последнего результата (2.2.5) получим формулу для расчета комплексного (двухстороннего) спектра сигнала s(t) из задачи 1 предыдущего раздела. Приведенный на рис. 1 сигнал (см. стр. 4) может рассматриваться как периодическое
(с периодом Тп = 2Т) повторение видеоимпульса s4(t), а значит, в соответствии с (2.1.3), его комплексный спектр может быть (с
учетом замен Tп = T/2, Ω = π/Т ) рассчитан по формуле
|
|
|
1 |
|
|
|
|
1 |
|
|
2 S |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||
c |
|
= |
|
|
n = |
|
|
|
|
|
1 |
- cos |
|
Т |
= |
||||
|
|
G |
|
|
|
|
|
||||||||||||
|
n |
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Тп |
|
|
|
|
|
|
|
|
T |
|
|
||||||
|
|
|
|
|
|
|
2Т Т n / T |
|
|
|
|
|
|||||||
|
|
|
|
|
|
= |
S0 |
1 cos n |
|
|
|
|
|
|
(2.2.6) |
||||
|
|
|
|
|
|
n 2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е. по спектральной плотности G4( ) удается получить тот же результат, что и ранее, но без какого-либо интегрирования.
Задача 2. Два видеоимпульса характеризуются спектральными характеристиками
G1(ω) = |
sin(10-4 |
) |
e |
j10-4 |
|
и G2(ω) = 1 / ( 10 |
4 |
+ j·ω ), В/Гц |
|
|
|
|
|
Определить протяженность интервала времени, на котором мгновенные значения и того, и другого импульса отличны от нуля.
Решение
--14--
а) Для ответа на вопрос задачи следует преобразовать анализируемые сигналы во временную область. Если использовать для этого непосредственно (2.1.2), то для преобразования потребуется использовать ряд табличных интегралов. В частности, используя обозначение τ = 10-4 с, для первого сигнала обратное преобразование Фурье (2.1.2) можно представить в виде
|
1 |
|
sin( ) |
|
|
||
s1(t) = |
|
|
|
|
|
ej |
e j td = |
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
sin( ) e |
j (t ) |
|
|
1 |
|
sin( ) cos( (t )) |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
= |
|
Re |
|
|
|
|
|
|
|
d |
= |
|
|
|
|
|
|
|
d = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
sin( (t 2 ) ) |
|
|
|
sin( t ) |
|
|
|||||||
|
|
|
= |
|
|
|
|
|
|
|
|
d - |
|
|
d |
|
||||
|
|
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
||||||
Но в соответствии с таблицей определенных интегралов (см.,
например, [4, c. 111])
sin( ) |
|
||
|
|
d = 0.5 · π · sign(τ), |
(2.2.7) |
|
|||
0 |
|
|
|
где sign(·) - функция взятия знака числа, поэтому при t < -2·τ и при t > 0 два образующих сигнал s1(t) интеграла компенсируют друг друга, а при t+2×τ>0 и t<0 знаки интегралов противоположны и вместо компенсации наблюдается удвоение
1 |
|
|
|
|
1 |
|
||||
s1(t) = |
|
|
|
sign(t 2 )- |
|
sign(t) |
= |
|
· [ 1 - (-1) ] = 0.5 В. |
|
2 |
2 |
2 |
4 |
|||||||
|
|
|
|
|
|
|||||
Итак, сигнал s1(t) имеет вид прямоугольника, лежащего между моментами времени tн = -2τ и tк = 0 (см. рис. 7а). Используя функцию rect(·) (см., например, [2, с. 27]), этот сигнал можно записать аналитически s1(t) = 0,5 · rect( 0,5 + t / 2τ ), В.
б) Отметим, однако, что функция sinc(x) = sin(x) / x при любых спектральных преобразованиях приводит к некоторой функции rect(·), причем если горизонтальные размеры функций измерять
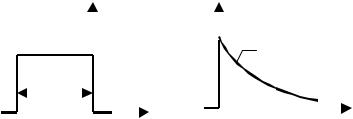
--15--
в секундах и герцах, а координату первого нуля функции sinc(x) обозначить через x0, то высота получаемого прямоугольника будет равна x0, а ширина - 1/x0 (см., например, [1, c. 37; 2, с. 58]). В соответствии с этим правилом модулю спектральной плотности G1(ω) равному τ·sinc(τ·ω), где τ = 10-4 с, и обращающемуся в ноль на частоте f0 = 1 / 2·τ соответствует во времен-
ной области прямоугольный видеоимпульс длительности tк - tн = 1 / f0 = 2τ, принимающий на этом временном интервале значе-
ние s0 = τ·f0 = 1/2. Сомножитель же ej10-4 , входящий в состав G1(ω), в соответствии с теоремой о временном сдвиге сигнала [1, с. 31; 2, с. 53] свидетельствует о
|
|
s1(t), В |
|
|
1 |
|
s2(t), В |
|||
|
|
|
|
|
||||||
|
|
|
|
0,5 |
|
|
1·exp(-104·t) |
|||
а) |
|
|
|
|
б) |
|
||||
|
2·τ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2·10-4 |
0 t, с |
0 |
t,с |
||||||
Рис. 4
сдвиге сигнала s1(t) относительно начала координат на величину tз = - τ. Таким образом, искомый сигнал действительно определяется выражением s1(t) = 0,5 · rect( 0,5 + t / 2τ ), однако в последнем случае для получения результата не потребовалось осуществлять никакого интегрирования.
в) Для преобразования во временную область спектральной плотности G2(ω) можно аналогично пункту "а" воспользоваться математическим справочникам, содержащим таблицу интегралов, но если такой справочник по каким-то причинам недоступен, то целесообразно от преобразования Фурье перейти к преобразованию Лапласа. На основании [1, с. 59] функции G2(ω) можно поставить в соответствие изображение S2(p) =
--16--
= 1 / (α + p), где α = 104 рад/c, и, следовательно, сигнал s2(t) определяется обратным преобразованием Лапласа для S2(p),
1 |
|
|
j |
e |
pt |
||
т. е. интегралом вида s2(t) = |
|
|
|
|
|
|
dp. В соответствии с |
2 j |
|
|
|||||
|
|
j |
p |
||||
[1, с. 56] подобный интеграл, можно рассматривать как интеграл по замкнутому контуру от функции f(p) = e+pt/(α + p), обладающей единственным простым полюсом p1 = -α. По теореме о вычетах [2; с. 140-141; 4, с.370] результат интегрирования f(p) равен значению вычета в точке p1, т. е.
s2(t) = lim (p ) f(p) = e-αt , при t ≥ 0. |
(2.2.8) |
p
Соответствующий (2.2.8) сигнал показан на рис. 7б.
г) Из сопоставления рисунков 7а и 7б видно, что сигналы s1(t) и s2(t) во временной области не перекрываются и длительность искомого интервала времени равна нулю.
Для лучшего усвоения материала разберите также задачи 2.16, 2.19, 2.28 и 2.29, приведенные вместе с краткими решениями в задачнике [5, с. 16-24].
Задача контрольной работы (№2):
Для представленного в таблице 1 (см. ниже) видеоимпульса
найти спектральную плотность (не забыть указать размерность);
определить во сколько раз отличаются по величине спек-
тральные составляющие на частотах ω = 0 и ω =
= ·103 рад/с, а также найти разность их начальных фаз;
предполагая, что указанные видеоимпульсы повторяются
с периодом Тп, записать общее аналитическое выражение для расчета амплитуды спектральных составляющих гармонического спектра получаемого периодического сигнала
sп(t).
--17--
Раздел 3. Временные и спектральные характеристики амплитудно-модулированных колебаний
3.1. Краткое теоретическое введение
Идеальным амплитудным модулятором называется устрой-
ство, преобразующее высокочастотный сигнал sн(t) = = S0 · cos( ω0·t + ψ0 ) в модулированное по амплитуде колебание sАМ(t) = S(t) · cos( ω0·t + ψ0 ) по правилу
S(t) = S0 + kАМ · sи(t), |
(3.1.1) |
где sи(t) - управляющий информационный сигнал; kАМ - параметр, называемый крутизной модулятора. Основным параметром амплитудно-модулированного колебания является коэффициент модуляции M, характеризующий наибольшее относительное отклонение амплитуды S(t) от ее значения в режиме
молчания, т.е. при sи(t) ≡ 0 |
|
|
kАМ |
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
||||||
M = |
max |
S(t)-S |
= |
max |
s |
и |
(t) |
. |
(3.1.2) |
|||||
|
|
|||||||||||||
|
|
t |
|
0 |
|
S |
|
t |
|
|
|
|
||
|
S0 |
|
|
0 |
|
|
|
|
|
|
||||
C позиций спектрального анализа наиболее простым являет-
ся случай тональной амплитудной модуляции, когда sи(t) =
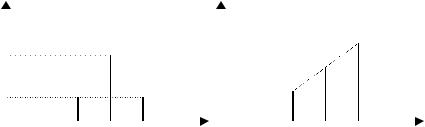
= Sи · cos( Ω·t + φ0 ), M = kАМ·Sи / S0. Соответствующий возникающему АМ-сигналу sАМ(t) = S0 · ( 1 + M·cos(Ω·t + φ0) )
cos(ω0·t + ψ0) спектр показан на рис. 8.
|
|
Sn, В |
|
|
Ψn, рад |
ψ0+φ0 |
||
|
|
S0 |
|
|
|
|||
|
|
|
|
|
ψ0 |
|||
|
|
|
|
|
|
|
||
|
|
S0·M/2 |
|
|
ψ0–φ0 |
|
|
|
|
|
ω, рад/с |
|
|
ω, рад/с |
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0 |
ω0–Ω ω0 ω0+Ω |
0 |
ω0–Ω ω0 ω0+Ω |
|||||
Рис. 5
--18--
Случаи нетональной амплитудной модуляции рассматрива-
ются в [1, с. 79-81; 2, с. 90-91; 3, с. 92] и в задачах (см. ниже).
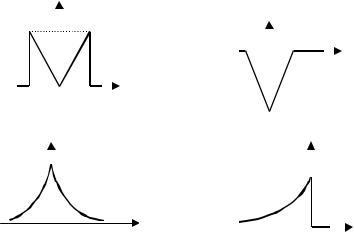
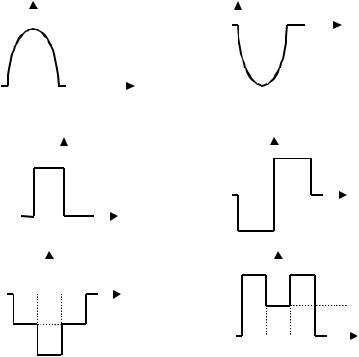
Таблица 1 индивидуальных заданий к задачам 2 и 3
N |
|
Импульс напря- |
Тп, |
N |
|
|
Импульс напря- |
Тп, |
||||||||||||||
|
|
|
жения |
|
|
мс |
|
|
|
|
жения |
|
|
|
мс |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
4 |
|
|
u(t), В |
2 |
2 |
|
|
|
|
u(t), В |
|
|
|
20 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-5 |
|
0 |
5 |
|
t,мс |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
0 |
|
|
1 |
t, мс |
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
u(t), В |
|
|
|
|
|
3 |
4 |
4 |
|
|
|
|
|
|
|
u(t),В |
20 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
4·exp(-10 ·|t|) |
|
|
2·exp(102·t) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
-1 |
0 |
|
1 |
t,мс |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
-0,01 |
0 |
t, с |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
--19--
5 |
|
|
|
|
u(t), В |
|
|
|
|
|
|
|
5 |
6 |
|
|
|
u(t), В |
|
40 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
|
|
|
|
|
|
0 |
20 |
t,мс |
|
|||||||
|
|
|
|
|
|
2 cos |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3·sin(π·50·t) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
-1,25 |
|
1,25 |
|
t, мс |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7 |
|
|
|
|
2 |
|
u(t), В |
|
10 |
8 |
|
4 |
|
u(t), В |
|
40 |
||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-20 |
|
t, мс |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
20 |
|
|
|
|
|
|||
|
-5 |
|
0 |
|
|
t, мс |
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
9 |
|
|
|
|
|
u(t), В |
|
|
|
|
|
|
16 |
10 |
|
3 |
|
u(t), В |
|
12 |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
-6 -2 |
|
2 |
6 |
|
t,мс |
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|||
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-45 -15 |
15 45 |
t,мс |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
--20--
3.2. Типовые задачи
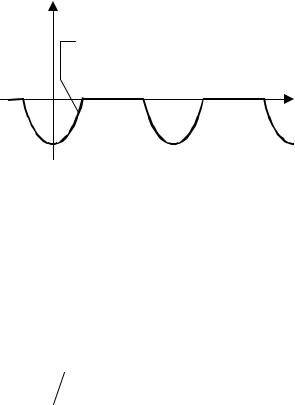
Задача 1. На идеальный амплитудный модулятор с крутизной kАМ=4 поступает несущее колебание sн(t) = 2·cos(2π106·t+π/3) (В)
и информационный сигнал, представленный на рис. 9. Определить коэффициент модуляции напряжения на выходе модулятора и спектральный состав формируемого АМ-сигнала.
sи(t), В
-0,3·cos(2π104·t)
-25 |
25 |
75 |
125 t, мкс |
-Sи
Рис. 6
Решение
а) Поскольку информационный сигнал имеет отрицательную полярность, то в процессе модуляции отклонение амплитуды формируемого колебания от исходного значения S0 будет наблюдаться лишь в сторону уменьшения. Максимальное по модулю
отклонение составит ΔS= kАМ |
max |
|
s |
и(t) |
= 4 · 0,3 = 1,2 В; в |
|
t |
|
|
|
|
|
|
|
|
результате коэффициент модуляции оказывается равным M =
|
|
|
|
|
= |
1,2 |
= 0,6. Соответствующий моду- |
||
= kАМ· max |
|
s |
и |
(t) |
S |
0 |
|||
|
|
||||||||
t |
|
|
|
|
2,0 |
|
|||
|
|
|
|||||||
лированный сигнал (без точного учета соотношения частот Ω
и ω0) показан на рис. 10.
