РТЦС-методичка

Для проверки правильности полученного результата достаточно подать мысленно на вход фильтра единичный отсчет и путем потактного анализа его работы убедиться, что отклик на подобное воздействие имеет вид s2(k) = { 2; 1; 1; 0,5; 0,5… }. Так как при подстановке в (8.2.2) значений r = 0, 1, 2, 3… получается та же последовательность отсчетов, то формула (8.2.2) действительно является общим аналитическим выражением импульсной характеристики анализируемого фильтра.

Задача 2. На дискретный фильтр с системной функцией H(z)= 1 / (1-0,1·z-1) воздействует последовательность отсчетов s1(k), в которой начальный отсчет равен единице, а каждый последующий в 10 раз меньше предыдущего. Определить реакцию фильтра на заданное воздействие.

Решение

а) Воздействующая на фильтр дискретная последовательность отсчетов может быть аналитически представлена выражением s1(k) = 0,1k.

Подставляя это выражение в прямое Z-преобразование (8.1.1) и применяя формулу для суммирования элементов бесконечной геометрической прогрессии, получим

--62--

б) Для определения Z-образа реакции дискретного фильтра на воздействие s1(k) воспользуемся правилом (8.1.4), в соответствии с которым

в) Для нахождения полюсов системной функции и числитель, и знаменатель S2(z) умножим на z в такой степени, чтобы в

знаменателе не осталось отрицательных степеней z (как и в задаче 1 для этого достаточно взять z2). Тогда

S2(z) = z2 / ( z - 0,1 )2.

Из последней формы записи очевидно, что S2(z) имеет полюс

z1 = 0,1 кратности m = 2. В результате формула (8.1.3'), определяющая значение вычета, записывается в виде

Итак, отклик s2(k) фильтра на воздействие s1(k) имеет вид, показанный на рис. 32. Убедиться в корректности найденного результата можно как и ранее путем потактного анализа состояния фильтра.

s2 (k)

1

0,2

0,03 0,004

Рис. 32. Отклик дискретного фильтра из задачи 2

--63--

Для более полного усвоения учебного материала разберите также решения задач 12.14, 12.27, 12.29, приведенные в задач-

нике [5, с. 184-191].

Задача контрольной работы (№8):

По заданномуZ-образудискретного сигнала

рассчитать и отобразить первые 5 отсчетов этого сигнала;

найти общее аналитическое выражение, определяющее значение произвольного k-го отсчета сигнала.

Z-образы анализируемых сигналов приведены в таблице ниже

--64--

Раздел 9. Анализ устойчивости цифровыхфильтров

9.1. К р а т к о е т е о р е т и ч е с к о е в в е д е н и е

Для обеспечения возможности применять дискретные фильтры на практике необходимо гарантировать их устойчивость. Устойчивым называется фильтр, сигнал на выходе которого однозначно определяется входным воздействием. Для устойчивости фильтра необходимо, в частности, чтобы после прекращения действия входного сигнала отклик фильтра носил затухающий характер. Математическим условием устойчивости фильтра является выполнение неравенства

r 0

где g( r ) - импульсная характеристика дискретного фильтра. При анализе устойчивости дискретных фильтров задаваемых их структурными схемами, правило (9.1.1) является не слишком удобным, так как требует, во-первых, нахождения импульсной характеристики (обычно бесконечной и весьма громоздкой), а, во-вторых, оценки сходимости ряда (9.1.1). В подобных случаях выгодно оценивать устойчивость непо-

средственно по системной функции фильтра:

Для устойчивости дискретного (цифрового) фильтра необходимо и достаточно, чтобы все полюсы его системной функции находились на z-плоскости внутри окружности единичного радиуса

В частности, нерекурсивные фильтры, т. е. фильтры у которых

bm = 0 для всех m ≥ 1, всегда устойчивы.

9.2. Т и п о в ы е з а д а ч и

Задача 1. Оценить устойчивость дискретного фильтра, функционирующего в соответствии с разностным уравнением

--65--

s2(k) = s1(k) - s1(k-1) + 0,5·s1(k-2) - 1,2·s2(k-1) + 0,45·s2(k-2).

Решение

а) Из разностного уравнения следует, что масштабирующие коэффициенты ветвей фильтра равны a0 = 1, a1 = -1, a2 = 0,5,

ar = 0 (r>2), b1 = -1,2, b2 = 0,45, bm = 0 (m>2), поэтому, в соот-

ветствии с (8.1.5), системную функцию данного фильтра можно представить в виде

б) Приравнивая знаменатель системной функции нулю и решая возникающее квадратное уравнение

z2 1,2 z -0,45 0 ,

можно убедиться, что системная функция анализируемого фильтра обладает полюсами z1 = +0,3 и z2 = -1,5. Поскольку последний полюс фильтра, очевидно, лежит за пределами единичной окружности, то данный фильтр неустойчив.

в) Для проверки правильности вынесенного решения найдем импульсную характеристику фильтра. На основании теоремы о вычетах (8.1.3) и с учетом формулы (8.2.1), ориентированной на работу с простыми полюсами (которыми и обладает анализируемый фильтр), импульсная характеристика фильтра будет определятся соотношением

= 0,29 0,3r + 4,25 ( 1,5)r . 1,8 1,8

Из полученного выражения видно, что знакопеременное слагаемое (-1,5)r с увеличением номера отсчета неограничен-

--66--

но возрастает по модулю, т. е. наблюдается самовозбуждение фильтра и, следовательно, этот фильтр - неустойчив.

Задача 2. Устойчив ли дискретный фильтр, структурная схема которого показана на рис. 33.

T 1,2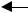

T

-1

Рис. 33. Структурная схема дискретного фильтра к задаче 2

Решение

а) В соответствии с (8.1.5) системная функция данного фильтра имеет вид

Приравнивая знаменатель последнего выражения нулю, опре-

деляем, что H(z)имеет полюса z1 = 0,6 + j·0,8 и z2 = 0,6 - j·0,8.

Поскольку | z1 | = | z2 | = 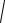0,62 0,82 = 1, то оба найденные

полюса лежат на единичной окружности. Таким образом, и для этого фильтра условие устойчивости (9.1.2) не соблюдается. Анализ фильтра во временной области показан на рис. 34. Из этого рисунка следует, что его импульсная характеристика обладает знакочередующимся незатухающим характером, что подтверждает неустойчивость фильтра.

--68--

Раздел 10. Оптимальная фильтрация сигнала заданной формы на фоне белого шума.

10.1. К р а т к о е т е о р е т и ч е с к о е в в е д е н и е

Задача оптимальной фильтрации сигналов заданной формы является по сути задачей обнаружения сигналов на фоне шума. В соответствии с этим оптимальным для обработки сигналов заданной формы является фильтр, обеспечивающий для обнаруживаемого сигнала в заранее выбранный момент времени наибольшее отношение сигнал/шум. В [1, с. 398-401; 2, с. 506-509; 3, с. 420-422] показано, что применительно к белому шуму подобным оптимальным устройством является согласованный фильтр, представляющий собой линейное аналоговое устройство с импульсной характеристикой

где s(t) - обнаруживаемый сигнал; t0 - момент времени, в который обеспечивается максимум отношения сигнал/шум (должен совпадать с моментом окончания сигнала или выбираться позже него); A - произвольная константа (свойства фильтра не зависят от A, так как изменение этого коэффициента в одина-

--69--

ковое число раз увеличивает как интенсивность полезного сигнала, так и среднеквадратическое значение шума на выходе фильтра).

Комплексный коэффициент передачи согласованного фильтра должен, очевидно, соответствовать (10.1.1) и может быть рассчитан по формуле

где G*s - величина комплексно-сопряженная спектральной

плотности обнаруживаемого сигнала.

Обеспечиваемое согласованным фильтром отношение сигнал/шум не зависит от формы обнаруживаемого сигнала, а определяется лишь его энергией и спектральной плотностью мощности помехи. Квадрат отношения сигнал/шум (отношение сигнал/шум по мощности) на выходе согласованного фильтра в момент времени t0 равен

где N0 - спектральная плотность мощности шума, а Эs - энергия полезного сигнала определяемая соотношением

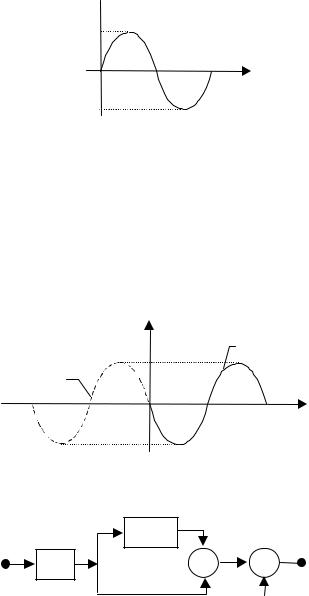
Задача 1. Предложить структурную схему фильтра, согласованного с видеоимпульсом, показанным на рис. 35, и определить форму отклика этого фильтра на сигнал s1(t).

--70--

s1(t)

U0

-U0

Рис. 35. Обнаруживаемый видеоимпульс к задаче 1

Решение

а) На основании (10.1.1) импульсная характеристика фильтра, согласованного с сигналом s1(t) должна иметь вид, показанный на рис. 36, чему соответствует аналитическое выражение

Один из возможных способов реализации подобной импульсной характеристики предложен на рис. 37.

Рис. 36. Импульсная характеристика фильтра, согласованного с сигналом s1(t)

sin(2π·t/τ)

Рис. 37. Структурная схема фильтра, согласованного с сигналом s1(t)