19.Производные и дифференциалы высших порядков. Производные высших порядков от функции заданной параметриески.

I)Предположим, что функция f'(x) является дифференцируемой в некоторой точке x интервала (a,b), то есть имеет в этой точке производную. Тогда данную производную называют второй производной и обозначают f⁽²⁾(x), f''(x) или y⁽²⁾, y''(x). Аналогично можно ввести понятие второй , третьей и т. д. производных. По индукции можно ввести понятие n- ой производной:

y(n) = (y(n-1))'.

(6)

Функцию, имеющую на некотором множестве конечную производную порядка n, называют n раз дифференцируемой на этом множестве. Методика нахождения производных высших порядков предполагает умение находить производные первого порядка, о чем говорит формула (6).

Если u(x), v(x) две дифференцируемые функции, то для нахождения производной их произведения справедлива формула Лейбница

(u(x)v(x))⁽ⁿ⁾ = u(n)v+nu(n-1)v'+(n(n-1)/2)u(n-2)v''+...+ uv(n) =

= _{k =} 0ⁿC_n^ku(n-k)v(k),

где

C_n^k = (n(n-1)(n-2)...(n-k+1))/k!, u(0) = u, v(0) = v.

Данная формула Лейбница особенно эффективна в случае, когда одна из перемножаемых функций имеет конечное число отличных от нуля производных и легко вычислить производные другой функции.

II) Пусть x =  (t),y =  (t), t [a,b] - достаточно гладкие функции. Тогда говорят, что функция задана параметрически. Примером параметрически заданной функции является уравнение окружности: x = acos t,y = asin t, t [0,2]. Рассмотрим вопрос о нахождении производных y = y(x) по переменной x.

В силу свойства инвариантности формы первого дифференциала следует, что y' = dy/dx, dy = '(t)dt, dx = '(t)dt. Поэтому

y'(x) = '(t)/'(t).

Используя формулу для второго дифференциала, получим

y(2)(x) = d(y'(x))/dx = ( '(t)/ '(t))'dt/ '(t)dt =

= ( ''(t)  '(t)- ''(t) '(t))/( '(t))³.

Чтобы вычислить третью производную, запишем y'''(x) в следующем виде

y'''(x) = d(y''(x))/dx.

20. Уравнения касательной и нормали к кривой.

Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M(x₀, y₀), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy. Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f'(x₀), то получаем уравнение y= f'(x₀)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x₀, y₀). Поэтому ее координаты должны удовлетворять у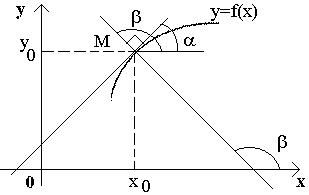равнению касательной:y₀= f'(x₀)·x₀ + b. Отсюда b=y₀– f'(x₀)·x₀. Таким образом, получаем уравнение касательной y= f'(x₀)·x +y₀ – f'(x₀)·x₀ или y = f '(x₀)·(x – x₀) + f(x₀) Если касательная, проходящая через точку М(x₀,y₀) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение x= x₀. Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль. Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке. Из определения нормали следует, что ее угловой коэффициент k_n связан с угловым коэффициентом касательной k равенством:. Учитывая, что нормаль также как и касательная проходит через точкуM(x₀, y₀), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:Ясно, что если касательная параллельна осиOx, т.е.f'(x₀) = 0 и ее уравнение имеет вид y= y₀, то нормаль в этой же точке будет перпендикулярна оси Ox. Значит, ее уравнение имеет вид x= x₀.