16. Производные основных функций: sin(X), cos(X), tg(X), ctg(X), lg(X), arcsin(X), arcos(X), arctg(X), arcctg(X), ax, xn и гиперболических функций.

ln^’ x=1/x

(a^x)^’= (a^x)*ln a.

Производные гиперболических функций:

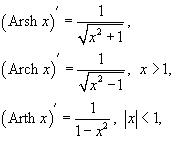
17. Производная функции заданной параметрически.

Пустьx=x(t), y=y(t), тогда какому-то x, будет соответствовать какое-то значение t (t=f(x)), поэтому t будет соответствовать y и можно говорить, что y является функцией x (y=(x)), можно говорить, что y^’_x. Заданная функция называется параметрически заданной функцией.

Теорема: Пусть y(x) задана параметрически уравнением (выше) предположим, что эти функции дифференцируемы и функция x=x(t) имеет обратную функцию t=f(x), тогда y^’_x, будет y^’_x=(y^’(t))/(x^’(t)). Из системы следует, что y=y(f(x)), y^’_x= y^’(t)*f^’(x) (По теореме производных обратной функции).

18. Дифференциал функции, его геометрический смысл. Свойства дифференциала.

Рассмотрим функцию y = f(x), дифференцируемую в данной точке x. Приращение  y ее представимо в виде

 y = f'(x) x + ( x)  x,

где первое слагаемое линейно относительно  x, а второе является в точке  x = 0 бесконечно малой функцией более высокого порядка, чем  x. Если f'(x) 0, то первое слагаемое представляет собой главную часть приращения  y. Эта главная часть приращения является линейной функцией аргумента  x и называется дифференциалом функции y = f(x). Если f'(x) = 0, то дифференциал функции по определению считается равным нулю.

Определение: Дифференциалом функции y = f(x) называется главная линейная относительно  x часть приращения  y, равная произведению производной на приращение независимой переменной dy = f'(x) x (4). Заметим, что дифференциал независимой переменной равен приращению этой переменной dx =  x. Поэтому формулу для дифференциала принято записывать в следующем виде: dy = f'(x)dx. Выясним каков геометрический смысл дифференциала. Возьмем на графике функции y = f(x) произвольную точку M(x,y) (рис21.). Проведем касательную к кривой y = f(x) в точке M, которая образует угол  с положительным направлением оси OX, то есть f'(x) = tg . Из прямоугольного треугольника MKN KN = MNtg xtg  = f'(x) x, то есть dy = KN. Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение  x. Отметим основные свойства дифференциала, которые аналогичны свойствам производной. d c = 0; d(c u(x)) = c d u(x); d(u(x)  v(x)) = d u(x)  d v(x); d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x); d(u(x) / v(x)) = (v(x) d u(x) - u(x) d v(x)) / v²(x). Укажем еще на одно свойство, которым обладает дифференциал, но не обладает производная. Рассмотрим функцию y = f(u), где u =  (x), то есть рассмотрим сложную функцию y = f((x)). Если каждая из функций f и  являются дифференцируемыми, то производная сложной функции согласно теореме (функция y = f((t)) дифференцируема в точке t, причем справедлива формула (f((t)))' = f'(x)'(t).) равна y' = f'(u)· u'. Тогда дифференциал функции dy = f'(x)dx = f'(u)u'dx = f'(u)du, так как u'dx = du. То есть dy = f'(u)du (5). Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала. Замечание. Отметим, что в формуле (4) dx =  x, а в формуле (5) du яляется лишь линейной частью приращения функции u.