12. Определение производной. Механический и геометрический смысл производной.

Определение:

Предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Определение через предел:

Пусть в некоторой окрестности точки x₀R определена функция f:U(x₀)R→R. Производной функции fв точке x₀ называется предел, если он существует,

Механический смысл производной:

Пусть т.М движется неравномерно и прямолинейно пусть момент времени t точка находилась в положении А и за время ∆t переместилась в положение B, тогда за время ∆t точка прошла путь ∆s равная очевидно U_ср=∆s/∆t.

lim(∆s/∆t)=U(t)(при ∆t→0), то U(t)=s^’(t), s^’’=a(t).

Геометрический смысл производной:

Если функция f:U(x₀)→R имеет конечную производную в точке x₀ то в окрестности U(x₀) её можно приблизить линейной функцией.Функцияf₁ называется касательной к f в точке x₀ Число f ^‘(x₀) является угловым коэффициентом или тангенсом угла наклона касательной прямой.

13. Основные свойства производных.

1) Производная const=0, y=C, y^’=0;

2) Производная суммы равна сумме производных:

[U(x)+V(x)]^’=U^’(x)+V^’(x);

3)( U(x)/ V(x))^’=( U^’(x)*V(x)+U(x)*V^’(x))/V²(x);

4)(U(x)*V(x))^’=U^’(x)*V(x)+U(x)*V^’(x).

Пусть y(x)=U(x)*V(x)

14. Производная сложной функции. Теорема о связи непрерывности и дифференцируемости функции.

1)Теорема:

Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'_u, u'_x), тогда сложная функция y = y(u(x)) дифференцируема и y'_x = y'_u u'_x.

Доказательство:

Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем

2) Теорема:

Если функция  f(x) дифференцируема в некоторой точке  a, то она непрерывна в этой точке.

Доказательство:

По определению производной

Это предельное равенство означает, что выражение под знаком предела можно представить в виде

где  α(x)  – бесконечно малая функция при  x → a. Тогда

Следовательно, f(x)→f(a) при  x → a. Заметим, что дифференцируемость функции в некоторой точке означает ее гладкость в окрестности этой точки, что влечет за собой непрерывность функции в рассматриваемой точке. Однако обратное утверждение несправедливо – функция, обладающая свойством непрерывности в некоторой точке, не обязательно дифференцируема в этой точке.

15. Производная обратной функции. Производная показательно-степенной функции.

I) Производная обратной функции:

Теорема:

(Пусть функция f(x) непрерывна и строго монотонна в окрестности точке x₀. Если существует производная обратной x=f(y) в точке y₀, то существует производная самой функции в точке x₀ и y^’_x=1/x^’_y ).

Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функция y=f(x) дифференцируема, и y^’=1/g^’(y).

Доказательство:

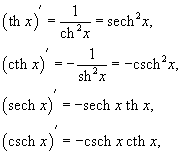Если аргументx получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом: Δx=g(y + Δy) − g(y). Тогда:

II) Производная показательно-степенной функции называется функция вида y[U(x)]^V(x).

1. Первый способ:

То есть вначале производная берется как от степенной функции, а потом как от показательной.

Замечание: Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а затем как от степенной, так как от перестановки слагаемых сумма не меняется:

2. Второй способ: