2.1 Вопросы для самопроверки

1. Каковы признаки возрастания и убывания функции?

2. Что называется экстремумом функции?

3. Сформулируйте необходимые и достаточные признаки существования экстремума функции.

4. Как найти интервалы выпуклости и вогнутости кривой и точки перегиба графика функции?

5. Что называется асимптотой кривой?

6. Каких видов бывают асимптоты графика функции и как их найти?

3 Неопределенный интеграл

Функция называетсяпервообразной функции еслиМножество первообразных функцииназывается неопределенным интегралом и обозначается.

Операции дифференцирования и интегрирования взаимнообратны:

,

поэтому нетрудно получить следующую таблицу интегралов:

1) (), 7),

2) , 8),

3) , 9),

4) , 10),

5) , 11),

6) , 12).

Не останавливаясь на непосредственном интегрировании по формулам, как на простейшем способе решения примеров, перейдём сразу к более сложным методам.

3.1 Метод замены переменного

Пусть требуется найти неопределенный интеграл от непрерывной функции

Рассмотрим некоторую функцию , которая имеет непрерывную производнуюи обратную функцию. (Например:монотонна). Тогда справедлива формула:

. (3.1.1)

В некоторых ситуациях удается подобрать функцию так, что интеграл в правой части (3.1.1) оказывается проще, чем в левой части. Такой прием называетсяметодом замены переменной. На практике часто формулу используют в обратную сторону:

. (3.1.2)

Другими словами, если подынтегральное выражение может быть записано в форме левой части (3.1.2), то с помощью подстановки получаем более простой интеграл (3.1.1).

Пример 8 .

Решение.

.

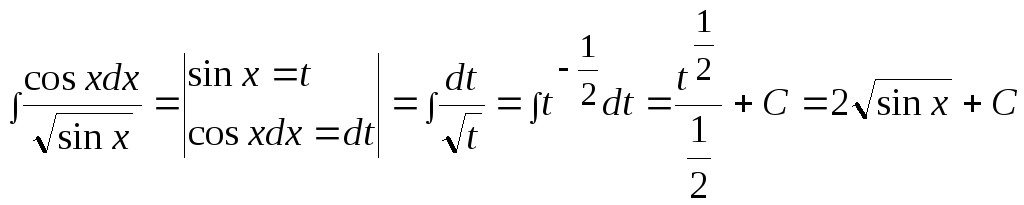Пример 9 .

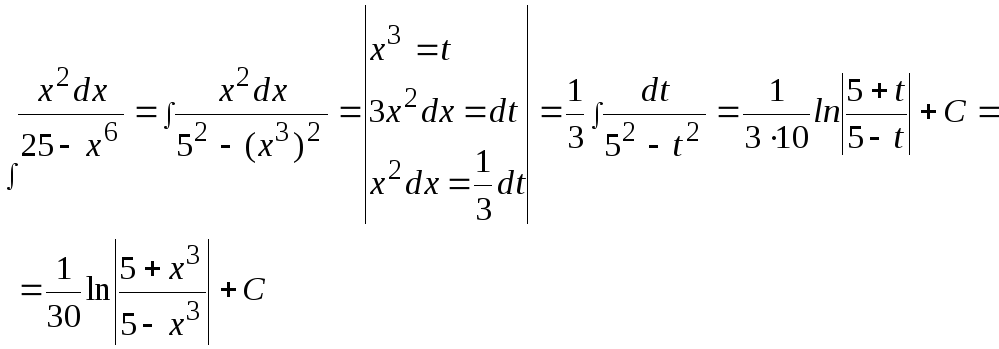
На практике часто используется следующая простая формула:

,

где - первообразная функции.

Пример 10. .

Пример 11. .

Пример 12. .

3.2 Интегрирование по частям

Формула интегрирования получается почленным интегрированием формулы производной произведения.

.

Смысл формулы заключается в том, что производная перебрасывается с одного множителя не другой и интеграл при этом может оказаться проще, чем исходный.

Можно выделить по крайней мере два класса интегралов, для которых применима формула интегрирования по частям.

I.

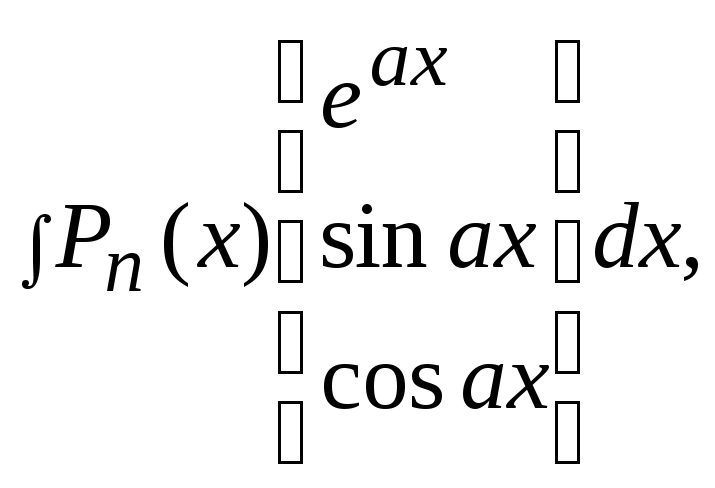
где - многочлен степени. В качественужно взять, а=- другой сомножитель.

При этом формулу приходится применить столько раз, какова степень многочлена.

II. .

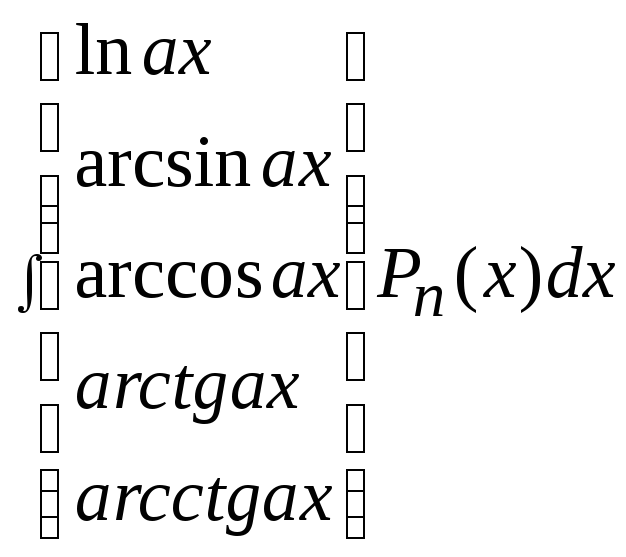В этом случае, наоборот, следует положить =.

Рассмотрим применение указанной схемы.

Пример 13.

.

Это интеграл первого типа, поэтому:

==

==

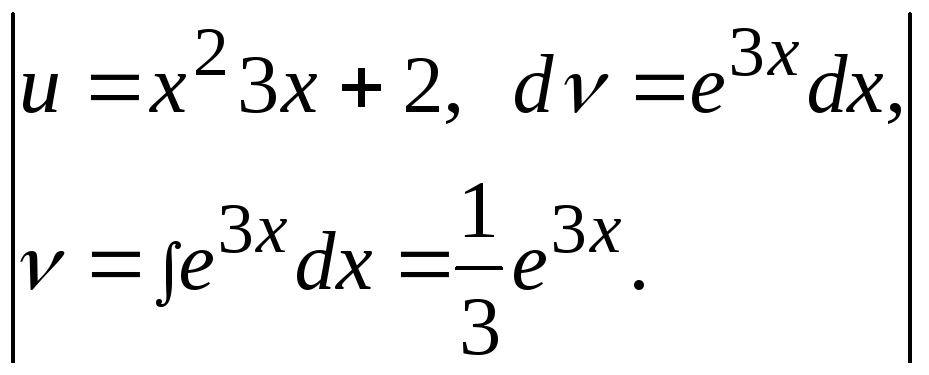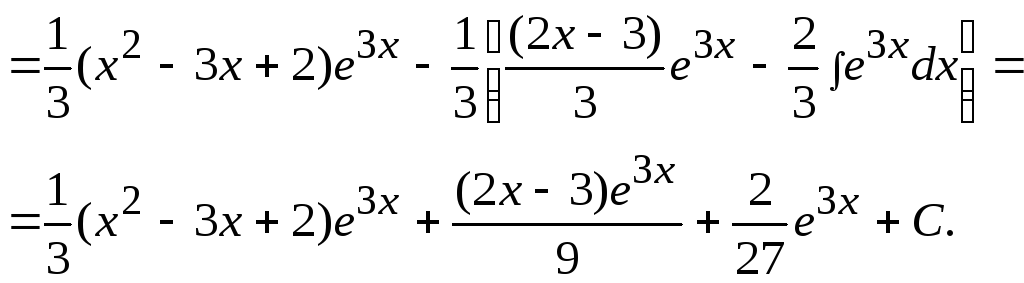
Пример 14. .

Решение.

Это интеграл второго типа, поэтому имеем:

.

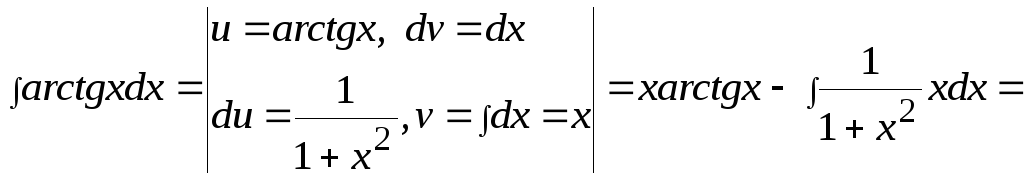
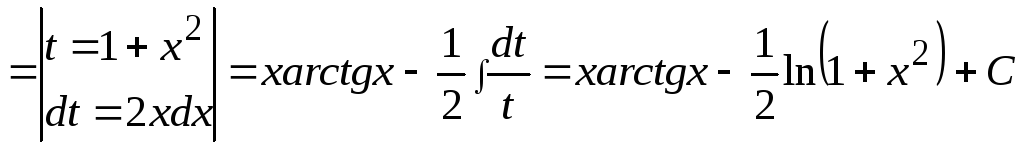Заметим, что при использовании формулы интегрирования по частям приходится восстанавливать функцию по ее дифференциалу. Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию.

Формула интегрирования по частям может хорошо сработать и в других случаях.

Пример 15 .

.

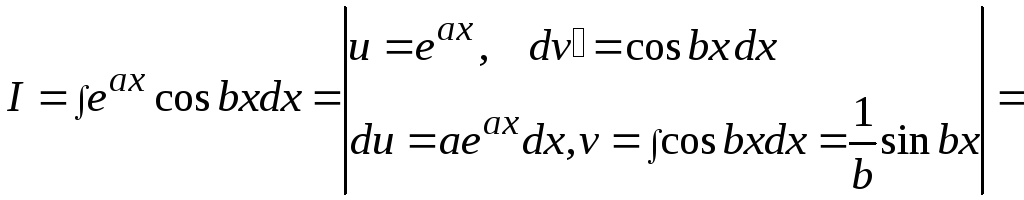
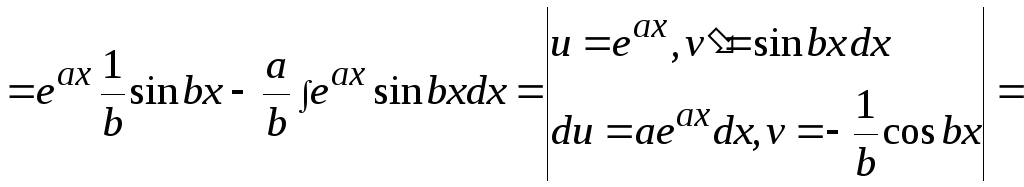
Получили уравнение относительного исходного интеграла I. Вынося I за скобку, получим

,

откуда

.

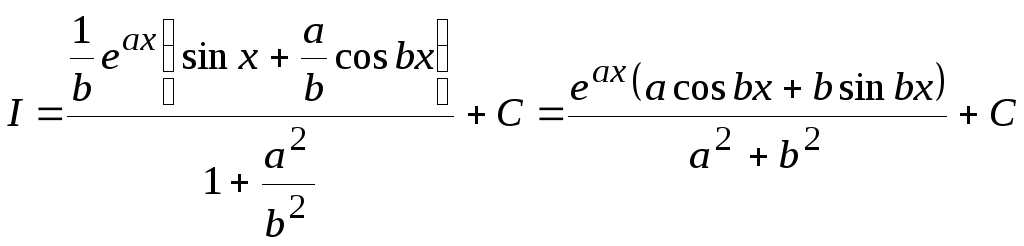3.3 Интегрирование выражений, содержащих квадратный трехчлен.

К этому типу интегралов относятся интегралы вида:

;

;

Мы увидим в дальнейшем, что без умения находить такие интегралы, мы не сможем вычислять интегралы от рациональных дробей.

Сначала научимся находить более простые интегралы видов и.

Трудность заключается в наличии слагаемого bx. Если бы его не было, то, вынося за знак интеграла , получили бы интеграл вида (11) или (12). Решить проблему можно выделением полного квадрата.

Пример 16 .

Решение.

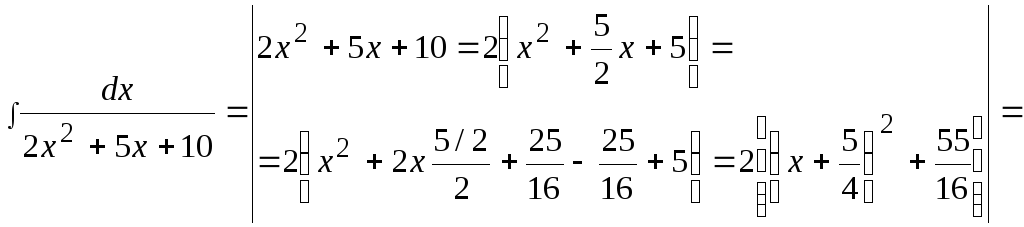
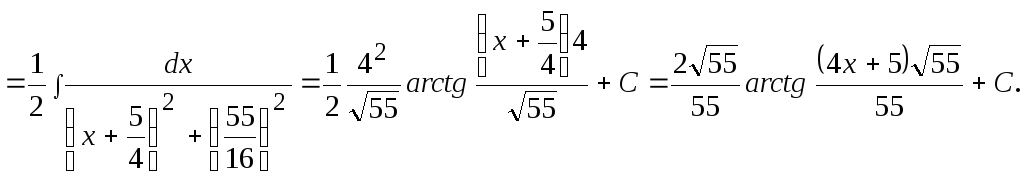
Пример 17 .

Решение.

.

Пример 18.

Решение.

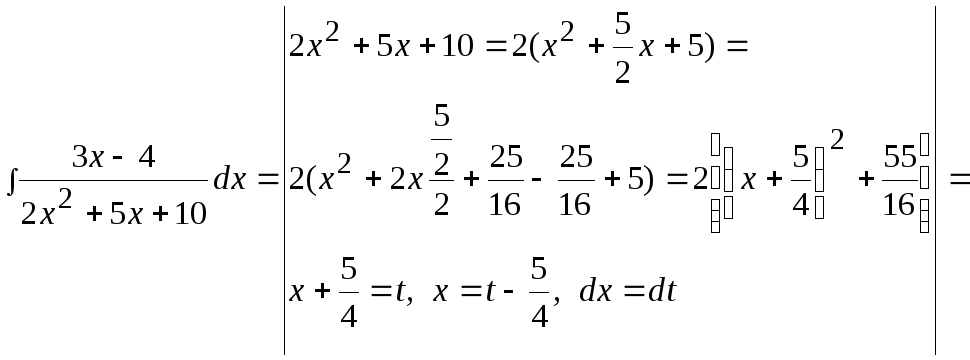
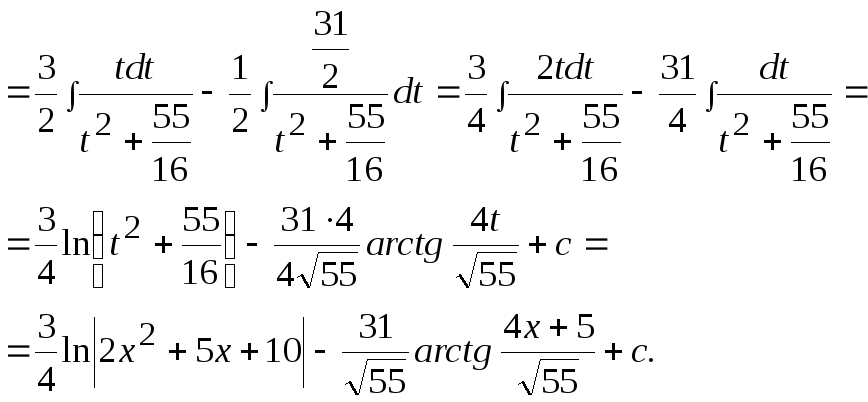
Пример 19 .

Решение.

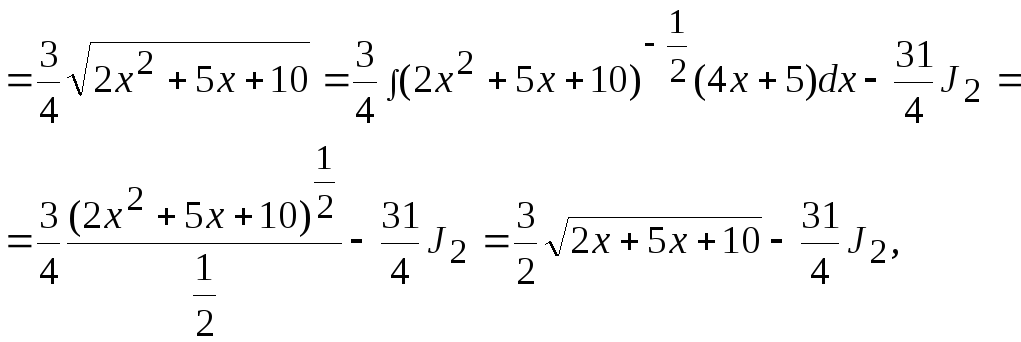
где - интеграл, рассмотренный в примере 17.