1 Производная функции

Понятие производной функции является одним из основных в математике и широко применяется в различных областях науки и техники.

Производной функции y=f(x) в точке хназывается предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю произвольным образом.

.

Процедура отыскания производной называется дифференцированием функции.

Справедливы следующие правила дифференцирования:

1. (с)=0 2. (u+v)=u+v3.(uv)=uv+uv

4. (сu)= сu5..

На основе этого определения могут быть выведены формулы для производных основных элементарных функций:

1. , в частности:;

2. , в частности:;

3. , в частности:;

4. ; 5.;

6. ; 7.;

8. ; 9.;

10. ; 11..

Особый интерес представляет производная сложной функции.

Если у=f(u), где u=, тогда у.

Пример 1 Найти производную функции: .

Решение.

Используя правило дифференцирования сложной функции, а также формулу нахождения производной степенной функции, получим:

.

Пример 2 Найти производную функции .

Решение.

Воспользуемся правилом дифференцирования произведения двух функций и формулами нахождения производной от показательной и логарифмической функции.

= == =

=.

Пример 3 Найти производную функции: .

Используем правило дифференцирования дроби и формулы нахождения производной от и степенной функции.

=

Пример 4Найти производную функции:.

Решение.

При нахождении производной неявно заданной функции продифференцируем обе части уравнения по переменной , имея в виду, чтоесть функция оти выразимиз полученного линейного относительноуравнения.

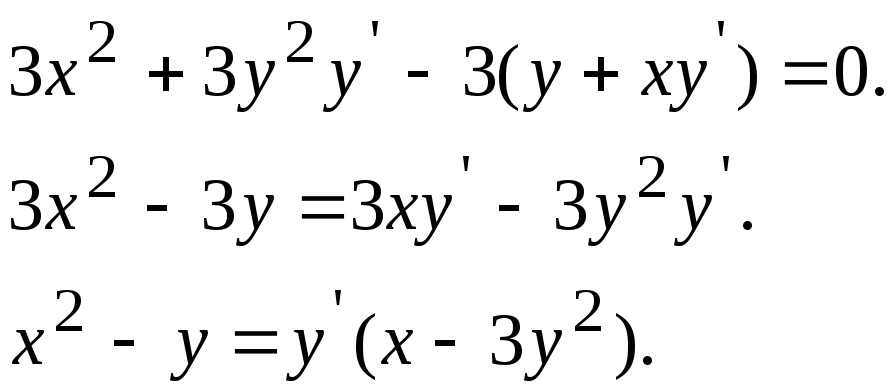
Если функция задана параметрическими уравнениями, то ее производная по переменнойнаходится по формуле.

Пример 5Найти производную функции:

Решение.

Поскольку ,, то

.

Пример 6Найти производную функции:.

Решение.

Применим метод логарифмического дифференцирования, для чего логарифмируем заданное выражение по основанию «», потом дифференцируем и находим у.

.

Дифференцируем:

=

=

Находим из полученного уравнения у:

.

0. Вопросы для самопроверки

1. Что называется производной функции?

1. Каковы правила нахождения производных от суммы, произведения, дроби, от постоянной величины?

2. Как найти производную сложной функции?

3. Правило дифференцирования функции, заданной неявно.

4. В чем заключается метод логарифмического дифференцирования?

2 Приложение производной к исследованию функции и построению ее графика

Методы дифференциального исчисления позволяют исследовать функции и строить их графики. Так, по знаку первой производной в интервале можно определить возрастание (убывание) функции, делать выводы о наличии или отсутствии экстремума функции. По знаку второй производной выделяем интервалы выпуклости (вогнутости) графика функции и точки перегиба ее графика.

Справедливы следующие теоремы:

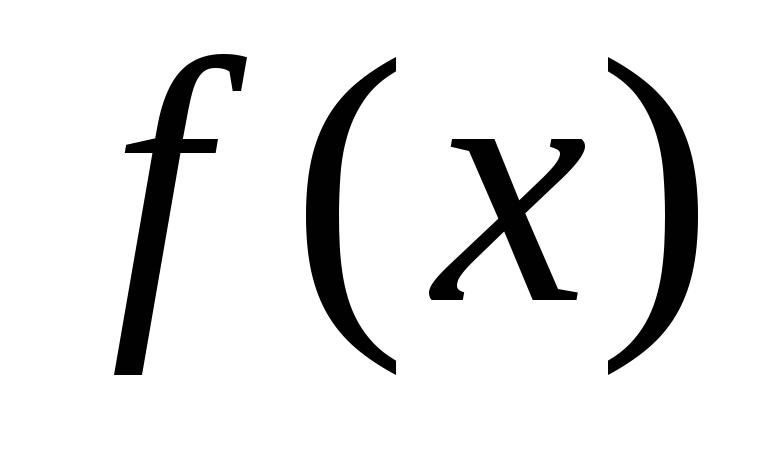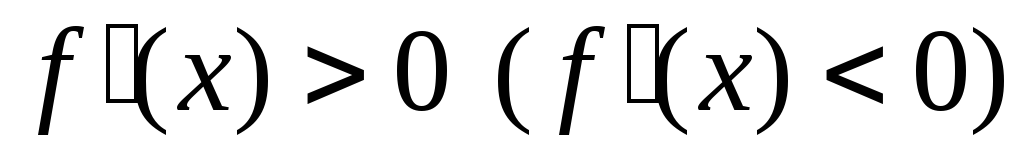1. Если функция дифференцируема на интервалеидля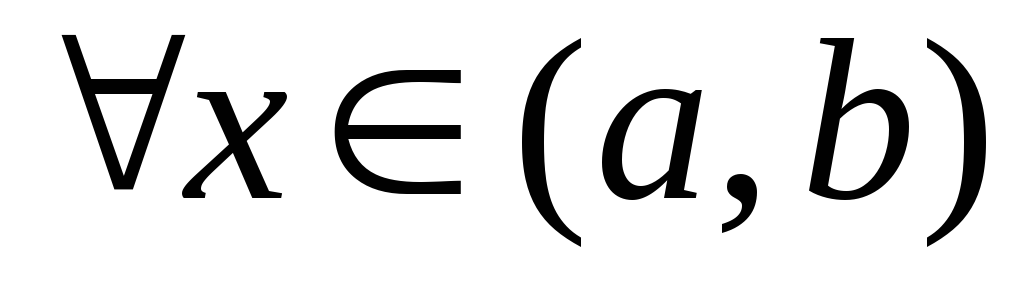, то эта функция возрастает (убывает) на интервале.

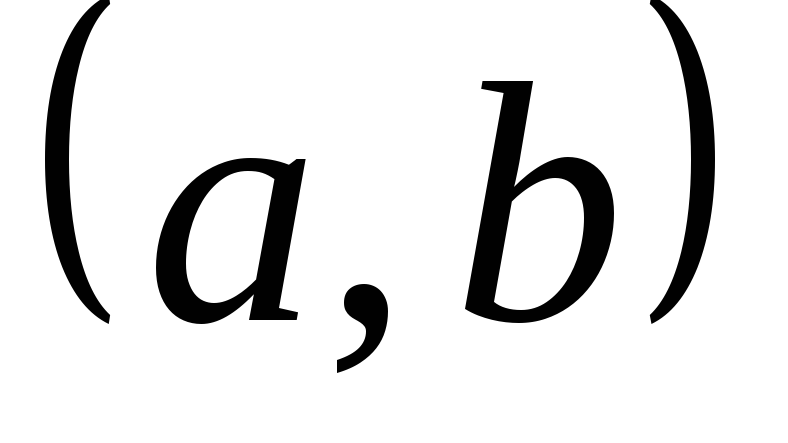2. Если дифференцируемая функция =имеет экстремум в точке х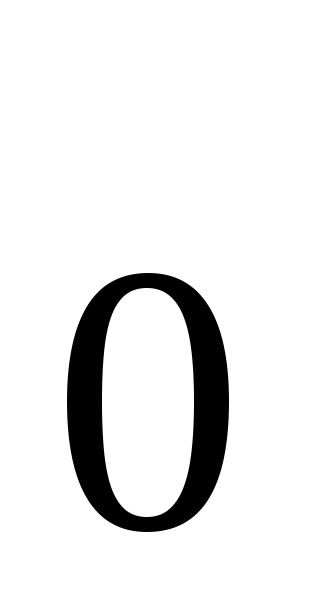, то ее производная в этой точке равна нулю:.

3. Если непрерывная функция =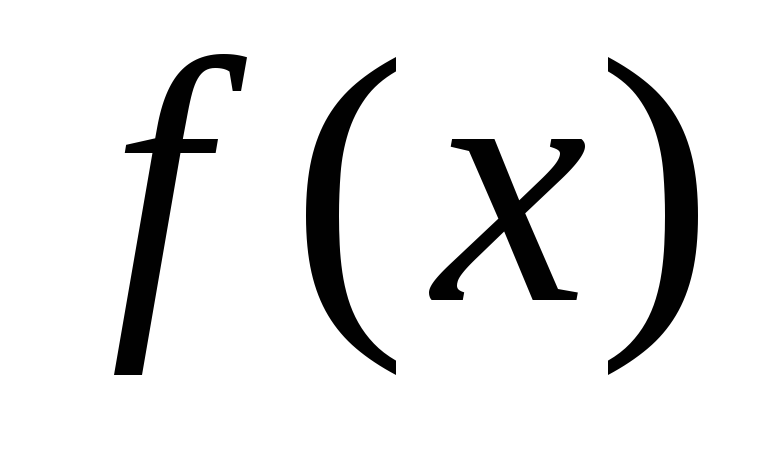дифференцируема в некоторой-окрестности критической точки х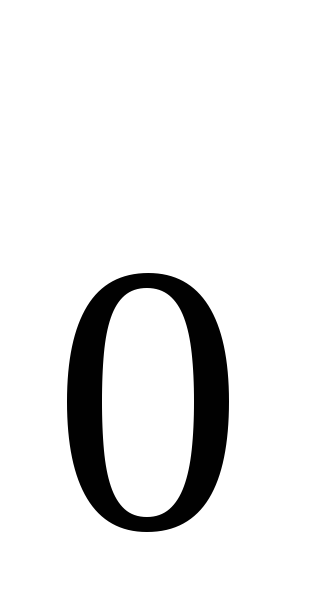и при переходе через нее (слева направо) производная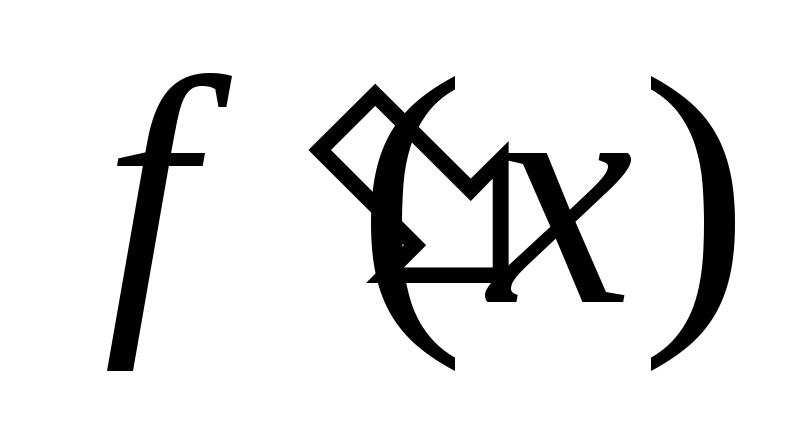меняет знак с плюса на минус, то х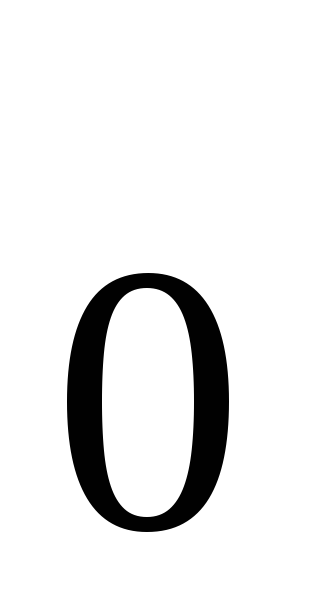- точка максимума; с минуса на плюс, то х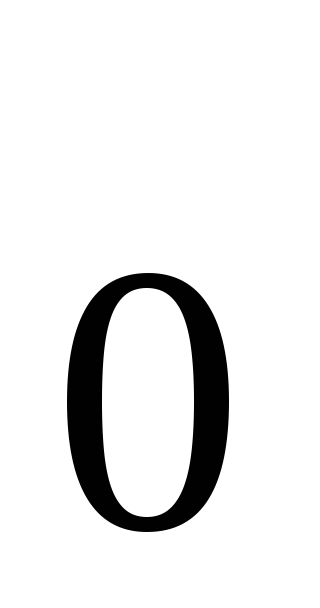- точка минимума.

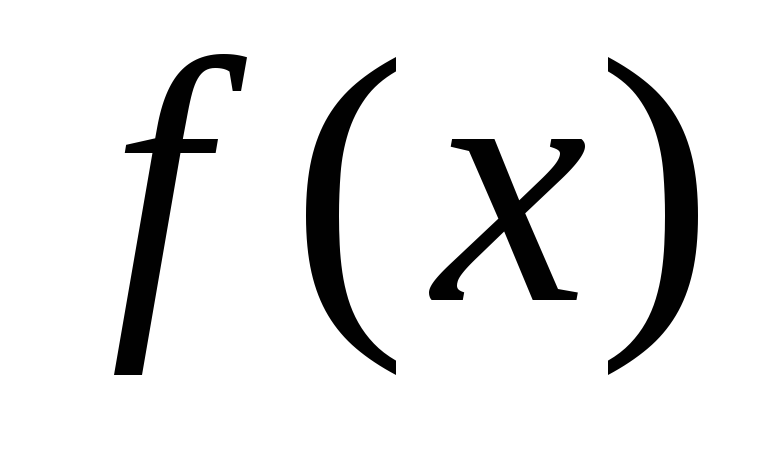4. Если функция =во всех точках интервала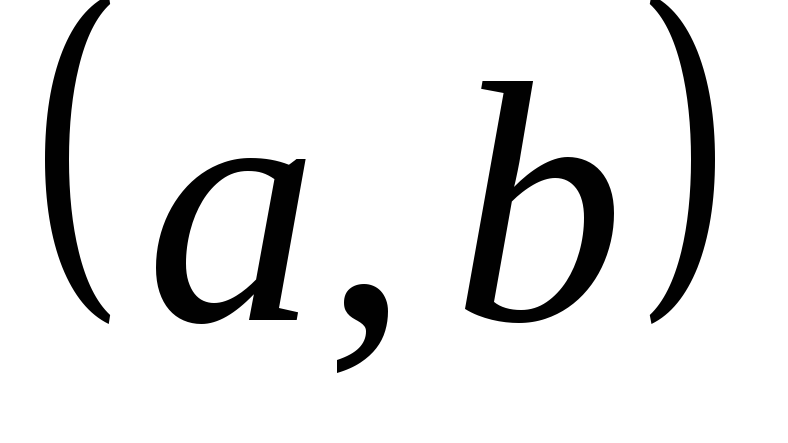имеет отрицательную вторую производную, то график функции в этом интервале выпуклый верх; если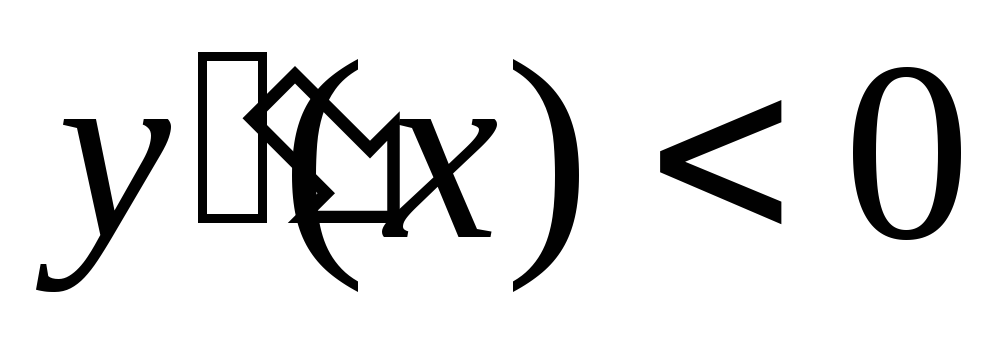, то график выпуклый вниз.

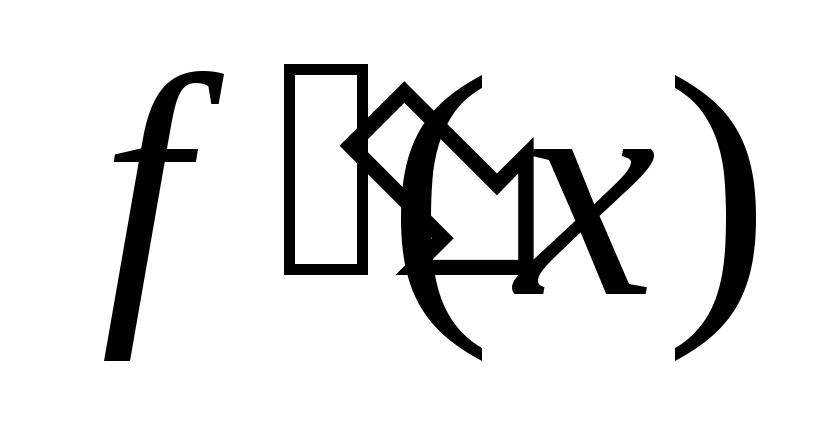5. Если вторая производная при переходе через точку х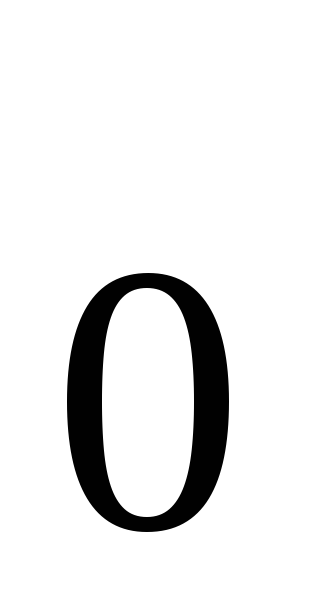, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х- точка перегиба.

Построение графика функции значительно облегчается, если известны его асимптоты.

Различают 2 вида асимптот:

а) Вертикальные, существующие в точках разрыва второго рода. Их уравнения имеют вид .

б) Наклонные: , где

,.

В частности, при наклонная асимптота становится горизонтальной и имеет уравнение.

При исследовании функции и построении ее графика полезно воспользоваться следующей схемой:

1. Найти область определения функции.

2. Найти точки пересечения графика с осями координат, если это возможно.

3. Найти асимптоты графика функции.

4. Найти интервалы монотонности и точки экстремума функции.

5. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.

На основании полученного исследования построить график.

Пример 7Исследовать функцию и построить ее график:

.

Решение.

1. Область определения.

.

2. Асимптоты графика:

а) вертикальная

б) наклонная , где

.

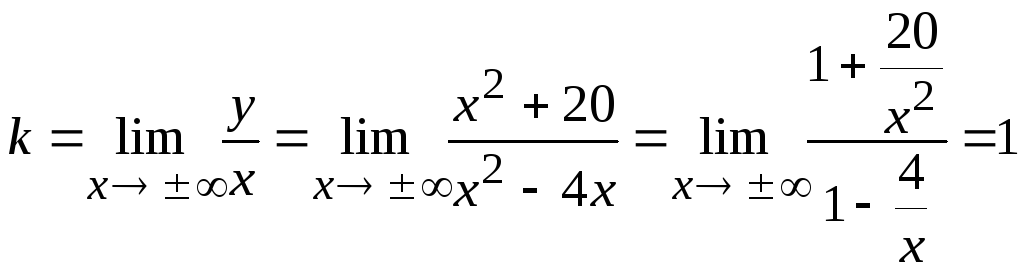3. Найдем производную функции.

;;.

.

Определим знак производной в промежутках:

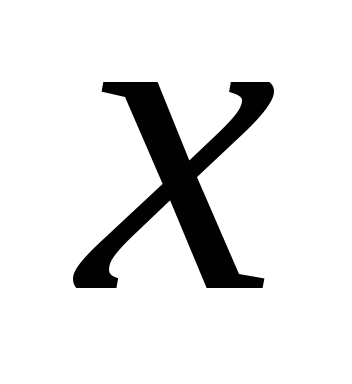
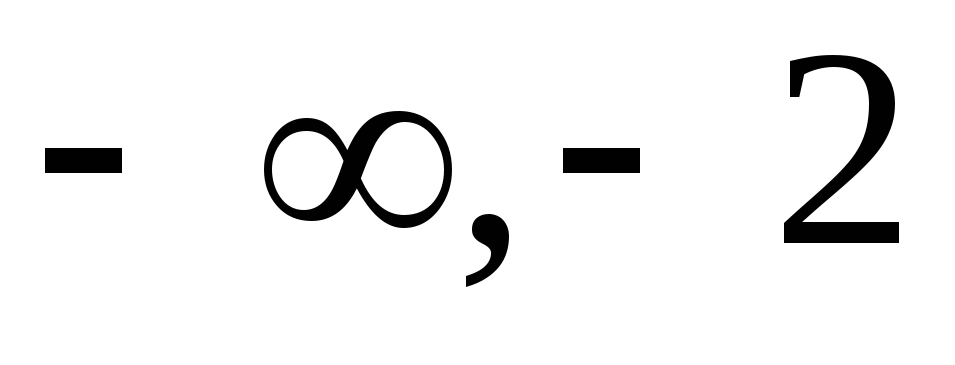	()	-2	-2, 4	4	(4, 10)	10	(10, +)
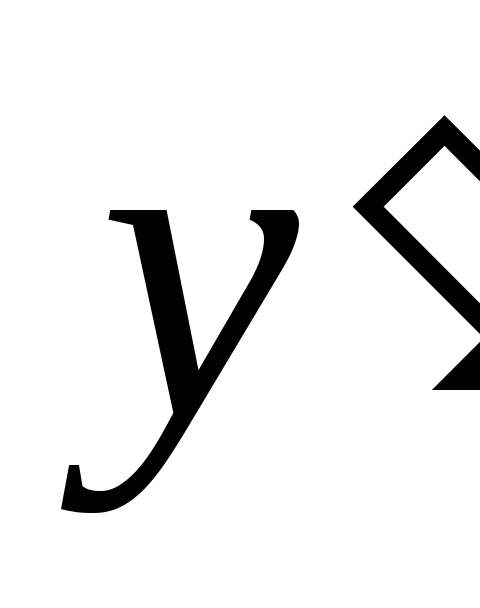
	+	0	-	не сущ.		0	+
		max				min

4. Найдем вторую производную функции.

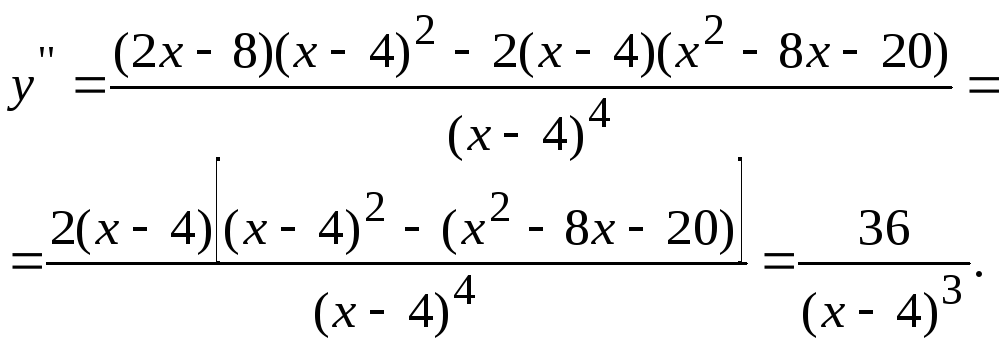
	()	4	(4, +)
	-	не сущ.	+

Точек перегиба графика функции нет.

П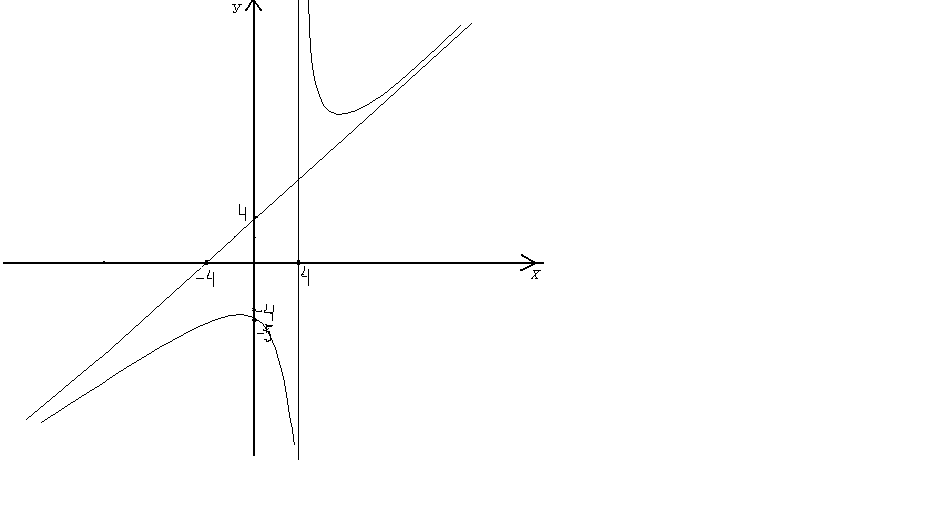о результатам исследования построим график функции.