
- •Билет №1.Числовые множества. Модуль. Элементарные ф-ции. Графики. Преобразование графиков.
- •Алгебраические:
- •Билет №2. Числовые последовательности. Определение предела числовой последовательности.
- •Билет №4. Свойства пределов числовой последовательности .
- •Билет №5. Пределы ф-ций. Свойства пределов ф-ций.
- •Билет №6. Бесконечно малые и бесконечно большие функции. Сравнение бм.
- •Сравнение бесконечно малых
- •Билет №9. Разрывы функций.
- •Точки разрыва первого и второго рода
- •Билет № 12.Понятие производной функции. Свойства производной.
- •Билет № 13 .Геометрический смысл производной.
- •Билет № 14. Уравнение касательной к графику.
- •Билет №15. Связь понятий. Дифференцируемость ф-ции в точке и ее непрерывность.
- •2) Существует ф-ция в каждой точке непрерывная и не в 1ой точке, не имеющая производной.
- •Билет №16.Дифференциал ф-ции. Произв. Суммы, произведения и отношения 2х ф-ций.
- •Правила дифференцирования.
- •Билет №22. Формулы Тейлора и Маклорена.
- •Билет №25. Исследование функции на выпуклость.
- •Билет №27. Предельные величины в экономике.
- •Билет №28. Эластичность спроса.
- •Билет №29. Оптимизационные задачи в экономике.
2) Существует ф-ция в каждой точке непрерывная и не в 1ой точке, не имеющая производной.
Производная стремится к бесконечности, когда касательная более перпендикулярна к оси Х.
Билет №16.Дифференциал ф-ции. Произв. Суммы, произведения и отношения 2х ф-ций.
Дифференциал - главная линейная часть приращения ф-ции. Если ф-ция y = f (x) 1го переменного х имеет при х = х0 производную, то приращение Δy = f (x0 + Δx) - f (x0) ф-ции f (x) можно представить в виде Δy = f' (x0) Δx + R,
где член R бесконечно мал по сравнению с Δх. Первый член dy = f' (x0) Δх
называется дифференциалом функции f (x) в точке x0. Из этой формулы видно, что дифференциал dy линейно зависит от приращения независимого переменного Δx, а равенство
Δy = dy + R показывает, в каком смысле Д. dy является главной частью приращения Δy.
1.Дифференциалом ф-ции называется произведение производной на приращение независимой переменной dy=f'(x)*Δx
Дифференциал независимой переменной равен приращению этой переменной =>
dy=f'(x)*dx или f'(x)=dy/dx
Также знак
дифференциала используется в
обозначении Лейбница для производной ![]() .
Это обозначение мотивировано тем, что
для дифференциалов ф-ции
.
Это обозначение мотивировано тем, что
для дифференциалов ф-ции ![]() и
тождественной ф-ции
и
тождественной ф-ции ![]() верно
соотношени
верно
соотношени![]()
2.Дифференциал функции
равен приращению ординаты касательной,
проведенной к графику в точке (х;у) при
изменении x на велечину Δx=dx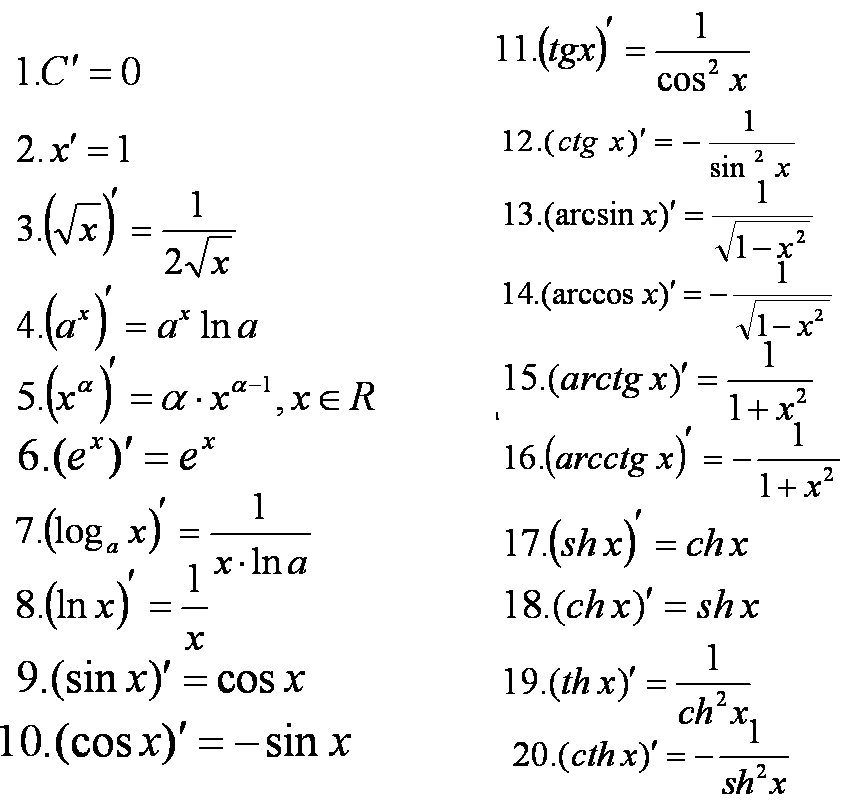
Правила дифференцирования.
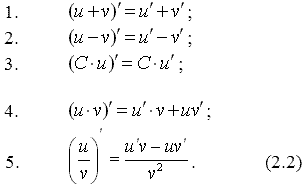
Билет № 17. Производная сложной функции. Пусть y = f(u), а u= u(x). Получаем ф-цию y, зависящую от аргумента x: y = f(u(x)). Последняя ф-ция называется ф-цией от ф-ции или сложной ф-цией.
Областью определения ф-ции y = f(u(x)) является либо вся область определения ф-ции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области определения ф-ции y= f(u).
Теорема. Если ф-ция u= u(x) имеет в некоторой точке x0 производную и принимает в этой точке значение u0 = u(x0), а ф-ция y= f(u) имеет в точке u производную y'u= f '(u0), то сложная ф-ция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x).
Таким образом, производная сложной ф-ции равна произведению производной данной ф-ции по промежуточному аргументу u на производную промежуточного аргумента по x.
Итак, чтобы продифференцировать сложную ф-цию y = f(u(x)), нужно взять производную от "внешней" ф-ции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" ф-ции по независимой переменной.
Если ф-цию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y'x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем y'x = y'u·u'x. Применяя эту же теорему для u'x получаем , т.е.
y'x = y'x · u'x· v 'x = f'u (u)·u'v (v)·v'x (x).
Примеры:
![]() :
:
![]()
![]() :
:
![]()
Билет № 18. Обратная функция и ее производная.
Функция ![]() является
обратной к ф-ции
является
обратной к ф-ции ![]() ,
если выполнены следующие тождества:
,
если выполнены следующие тождества:
![]() для
всех
для
всех ![]()
![]() для
всех
для
всех ![]()
Чтобы
найти обратную ф-цию, нужно
решить уравнение ![]() относительно
относительно ![]() .
Если оно имеет более чем 1 корень, то
ф-ции обратной к
.
Если оно имеет более чем 1 корень, то
ф-ции обратной к ![]() не
существует. Таким образом, функция
не
существует. Таким образом, функция ![]() обратима
на интервале
обратима
на интервале ![]() тогда
и только тогда, когда на этом интервале
она обратима
однозначно.
тогда
и только тогда, когда на этом интервале
она обратима
однозначно.
Для непрерывной
ф-ции ![]() выразить
выразить ![]() из
уравнения
из
уравнения ![]() возможно
в том и только том случае, когда
ф-ция
возможно
в том и только том случае, когда
ф-ция ![]() монотонна.
Тем не менее, непрерывную ф-цию всегда
можно обратить на промежутках её
монотонности. Например,
монотонна.
Тем не менее, непрерывную ф-цию всегда
можно обратить на промежутках её
монотонности. Например, ![]() является
обратной ф-цией к
является
обратной ф-цией к ![]() на
на ![]() ,
хотя на промежутке
,
хотя на промежутке ![]() обратная
функция другая:
обратная
функция другая: ![]() .
.
Пусть ![]() - дифференцируемая
ф-ция от аргумента x в некотором
интервале
- дифференцируемая
ф-ция от аргумента x в некотором
интервале ![]() .
Если в уравнении
.
Если в уравнении ![]() y
считать аргументом, а x - ф-цией, то
возникает новая ф-ция
y
считать аргументом, а x - ф-цией, то
возникает новая ф-ция ![]() ,
где
,
где ![]() - ф-ция
обратная данной.
- ф-ция
обратная данной.
Теорема о дифференцировании обратной функции
Для
дифференцируемой ф-ции с производной,
отличной от нуля, производная обратной
ф-ции равна обратной величине
производной данной ф-ции![]()
Для арксинуса:
![]()
![]()
Для арктангенса:
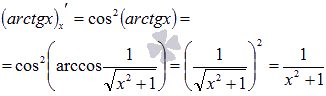
Билет 19. Теорема Лагранжа
Пусть
ф-ция ![]() дифференцируема в открытом промежутке
дифференцируема в открытом промежутке
![]() и сохраняет непрерывность на концах
этого промежутка. Тогда существует
такая точка
и сохраняет непрерывность на концах
этого промежутка. Тогда существует
такая точка ![]() ,
что
,
что![]()
Следствие
1. В частном случае,
когда ![]() ,
из теоремы Лагранжа вытекает, что
существует точка
,
из теоремы Лагранжа вытекает, что
существует точка ![]() ,
в которой производная ф-ции
,
в которой производная ф-ции ![]() равна
нулю:
равна
нулю: ![]() .
Это означает, что теорема Лагранжа
является обобщением теоремы Ролля.
.
Это означает, что теорема Лагранжа
является обобщением теоремы Ролля.
Следствие
2. Если ![]() во всех точках некоторого промежутка
во всех точках некоторого промежутка
![]() ,
то
,
то ![]() в
этом промежутке. Действительно, пусть
в
этом промежутке. Действительно, пусть
![]() и
и ![]() – произвольные точки промежутка
– произвольные точки промежутка ![]() и
и ![]() .
Применяя т. Лагранжа к промежутку
.
Применяя т. Лагранжа к промежутку ![]() ,
получим
,
получим
![]()
Билет №20. Правило Лопиталя.
Теорема
Лопиталя -
метод нахождения пределов
ф-ций, раскрывающий
неопределённости вида ![]() и
и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения ф-ций равен
пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения ф-ций равен
пределу отношения их производных.
Теорема Лопиталя:
-
 либо
либо 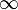 ;
; -
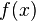 и
и 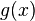 дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности 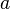 ;
; -
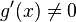 в
проколотой окрестности
в
проколотой окрестности 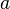 ;
; -
существует
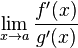 ,
,
тогда
существует ![]() .
.
Пределы также могут быть односторонними.
Билет №21. Производные высшего порядка. Формула Лейбница.
Пусть y = f(x) является дифференцируемой ф-цией. Тогда производная также представляет собой
ф-цию от x. Если и она является дифференцируемой ф-цией, то мы можем найти 2ую производную ф-ции f, которая обозначается в виде f''=(f')'=(dy/dx)=d/dx(dy/dx)=d2y/dx2
Аналогично, если f '' существует и дифференцируема, мы можем вычислить 3ю производную ф-ции f: f'''=(f'')'=d3y/dx3
Производные более высокого порядка (если существуют), определяются как f''''=(f''')'=d4y/dx4
Для нахождения производных высшего порядка можно использовать следующие формул
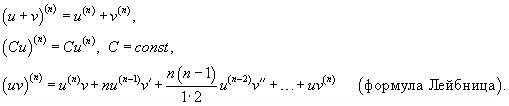
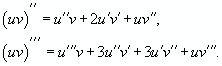
Ф-ла Лейбница для ![]() -ой
производной произведения 2 ф-ций -
обобщение правила дифференцирования произведения
(и отношения) 2х функций на случай
-ой
производной произведения 2 ф-ций -
обобщение правила дифференцирования произведения
(и отношения) 2х функций на случай ![]() -кратного
дифференцирования.
-кратного
дифференцирования.
Пусть
функции ![]() и
и ![]() —
— ![]() раз
дифференцируемые функции,
тогда
раз
дифференцируемые функции,
тогда![]() где
где ![]() — биномиальные
коэфф.
— биномиальные
коэфф.
(пример) В
случае ![]() ,
например, имеем:
,
например, имеем: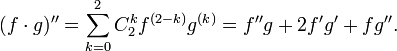
При ![]() получается
известное правило производной
произведения:
получается
известное правило производной
произведения:
![]()
