Билет №1.Числовые множества. Модуль. Элементарные ф-ции. Графики. Преобразование графиков.

трансцендентные:

• показательная и логарифмическая;

• тригонометрические и обратные тригонометрические.

Каждую элементарную ф-цию можно задать формулой, т.е. набором конечного числа символов, соответствующих используемым операциям. Все элем. ф-ции непрерывны на своей области определения.

Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.

График ф-ции - понятие, которое даёт представление о геометрическом образе ф-ции. Это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией: точка располагается (или находится) на графике функции  тогда и только тогда, когда .

[Элементарные] преобразования графиков функций - термин, используемый для обозначения линейных преобразований функции или её аргумента вида . Применяется также для обозначений операций с использованием модуля.

Билет №2. Числовые последовательности. Определение предела числовой последовательности.

Последовательность - числовая функция f_n, заданная на множестве натуральных чисел N.

Обозначается через a_n, (a_n), {a_n}. Если n  - натуральное число, а a_n - значение последовательности в тоске n, то n  - номер числа a,  а само число a_n - общий или n-ый член последовательности.

График - изолированное множество точек плоскости.

Способы задания числовых последовательностей:

1) формулой n-го члена.  1, 4, 9, 16, 25, 36, ...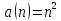 … 2) описания членов 2, 4, 6, 8, 10, ... 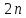... 1, 3, 5, 7, 9, ... 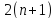... 3) рекуррентным 1, 1, 2, 3, 5, 8, 13, 21, ...  a_n = a_n-1 + a_n-2 , …

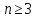Пример. Последовательность Фибоначчи. Проблема с кроликами: человек пару кроликов в загон, окруженный стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со 2го,  каждая пара кроликов производит на свет 1 пару?

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

(Ряд,  каждый член в котором - сумма двух предыдущих.)

Число А называется пределом числовой последовательности {a_n}, если для любого, сколь угодно малого положительного числа ε > 0, найдется такое число N (зависящее от ε, N=N_ԑ), что для всех членов последовательности с номерами n>N верно неравенство  .

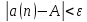Если это выполняется, то пишут 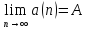или 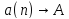при n∞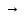

Последовательность может быть сходящаяся/расходящаяся.

Используя логические символы определение

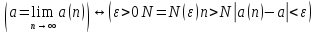
Смысл: для достаточно больших n члены последовательности {a_n} как угодно мало отличаются от числа a  (по абсолютной величине меньше, чем на число ԑ, каким бы малым оно ни было).

(Пример.: С ростом номера n число a_n становится все ближе к 1.  )

Билет №3. Бесконечно малые и бесконечно большие последовательности и их свойства.

Свойства бесконечно малых и бесконечно больших последовательностей

• Сумма 2х бесконечно малых последовательностей также бесконечно малая последовательность.

• Разность 2х бесконечно малых последовательностей также бесконечно малая последовательность.

• Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

• Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

• Любая бесконечно малая последовательность ограничена.

• Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.

• Если вся бесконечно малая посл-ность состоит из одинаковых элементов, то эти элементы - нули.

• Если некоторая бесконечно большая последовательность не содержит нулевых членов, то существует обратная последовательность , которая является бесконечно малой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера, и всё равно будет бесконечно малой.

• Если f(x) бесконечно малая последовательность, не содержащая нулевых членов, то сущ. обратная последовательность, которая является бесконечно большой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера, и всё равно будет бесконечно большой.

Теорема о переходе к пределу в неравенства: Если  или   на  и существуют и, то .

Теорема о 2х полицейских: Т: Пусть даны 3 последовательности: {Xn}, {Yn}, {Zn}. Причем Xn<=Yn<=Zn. При этом существует limXn=a=limZn (при n→∞), тогда limYn=a (при n→∞)

Доказательство:

1) Докажем, что Zn-Xn – бесконечно малая последовательность (бм)

Zn-Xn=Zn - a +a - Xn (Zn – a есть бм, + a – Xn – есть бм) => б.малая!

2) Докажем: Yn – Xn – бесконечно малая

0≤ Yn - Xn≤ Zn – Xn (а это бесконечно малая посл.) для любого E>0 существует N для каждого из которых n>N

|Zn – Xn| < E => |Yn – Xn| < E

Zn – Xn<E => Yn – Xn<E

3) Докажем: Yn – a – б.мал.

Yn - a = (Yn – Xn /есть б.мал.) + (Xn – a/ есть б.мал) – сумма б.малых есть б.малая.