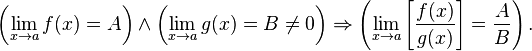Билет №4. Свойства пределов числовой последовательности .
Предел числовой последовательности - такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого удаление членов последовательности от данной точки становится меньше заранее заданной величины.
Аддитивность.
Предел суммы числовых
посл-стей есть сумма их пределов, если
каждый из них сущ-ет.
Однородность. Константу можно выносить из-под знака предела.
Предел
произведения числовых
посл-стей факторизуется на произведение пределов, если каждый из них сущ-ет.
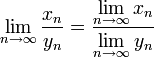
Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.
-
Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа.
-
Если некоторое число не превышает все элементы сходящейся последовательности, начиная с некоторого номера, то оно также не превышает и предела этой последовательности.
-
Если некоторое число строго превышает все элементы сходящейся последовательности, начиная с некоторого номера, то предел этой последовательности не превышает этого числа.
-
Если все элементы сходящейся последовательности, начиная с некоторого номера, строго превышают некоторое число, то это число не превышает предела этой последовательности.
-
Если, начиная с некоторого номера, все элементы одной сходящейся последовательности не превышают соответствующих элементов другой сходящейся последовательности, то и предел первой последовательности не превышает предела второй.
-
Для числовых последовательностей справедлива теорема о двух милиционерах.
-
Сходящаяся числовая последовательность имеет только 1 предел.
-
Замкнутость. Если все элементы сходящейся числовой последовательности лежат на некотором отрезке, то на этом же отрезке лежит и её предел.
-
Предел последовательности из одного и того же числа равен этому числу.
-
Замена или удаление конечного числа элементов в сходящейся числовой последовательности не влияет на её предел.
-
У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.
-
Если у последовательности
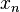существует
предел, то последовательность средних
арифметических 
имеет
тот же предел.
-
Если у последовательности чисел
существует
предел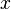 
,
и если задана функция 
,
определенная для каждого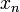 
и
непрерывная в точке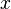 
,
то
Билет №5. Пределы ф-ций. Свойства пределов ф-ций.
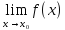=a
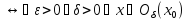
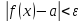
Значение
a
называется пределом функции f(x)
в точке
,
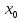если для любого
0
выполняется
неравенство
.
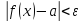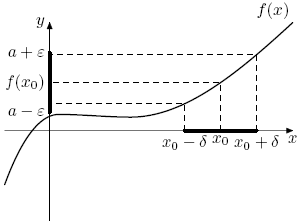
Значение a называется пределом функции 
в точке 
,
если для любой последовательности точек
,
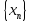стремящейся к 
,
но не содержащей 
в
качестве 1го из своих элементов (то есть
в проколотой окрестности 
),
последовательность значений функции
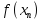стремится
к а.
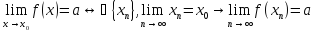
Значение 
называется пределом
функции 
в
точке 
,
если для любого наперёд взятого
положительного числа 
найдётся
отвечающее ему положительное число 
такое,
что для всех аргументов 
,
удовлетворяющих условию 
,
выполняется неравенство 
.
Односторонний
предел числовой
ф-ции в
точке - это специфический предел,
подразумевающий, что аргумент ф-ции
приближается к указанной точке с слева
или справа. Числовая ф-ция имеет предел
в точке <=> она имеет в этой точке
совпадающие левый и правый пределы.
Пусть даны ф-ции 
и 
.
-
Одна и та же функция в одной и той же точке может иметь только один предел
-
Сходящаяся функция локально сохраняет знак. Более обще,
где 
—
проколотая окрестность точки 
.
-
В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
-
Сходящаяся функция локально ограничена в окрестности предельной точки:
-
Отделимость от нуля функций, имеющих предел, отличный от нуля.
-
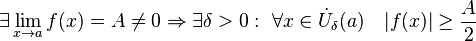
Операция взятия предела сохраняет нестрогие неравенства.
-
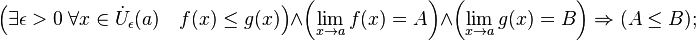
Правило двух милиционеров
-
Предел суммы равен сумме пределов:
-
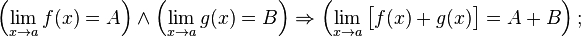
Предел разности равен разности пределов:
-
Предел произведения равен произведению пределов:
-
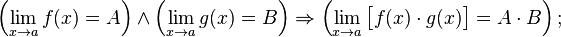
Предел частного равен частному пределов.
