Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

mu

.pdf

Скачиваний:

Добавлен:

29.05.2015

Размер:

1.72 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Вариант № 19

1. Найдите неопределённые интегралы:

∫

1.1.

−

−3

dx ;

1.2. ∫92−5 x dx ;
1.3. ∫		dx		;
	x 3	(2ln x −3)	4

1.4. ∫		dx			;
	arctg4 2x (1+ 4x2 )

2. Вычислите определённые интегралы:

1.5. ∫(9x −1) cos3xdx ;

1.6. ∫		dx		;
	1	−2x − x	2

1.7.∫sin2 (x 2) 9cos3 (x 2)dx ;

1.8.∫sin 3x 4 sin x 2 dx .

2.1. ∫4 e−2 x+7dx ;

0
1	xdx
2.2. ∫0	xdx	;
2.2. ∫0	(3x2 +1)2	;

2.3. ∫π x cos(x 2)dx ;

2.5. ∫4

, заменаx =

t −1

;

2x +1

0 1+

π3

1 −t2

2.6. ∫0

, замена x = tg

cos x =

;

2 +cos x

1 +t2

если

x ≤ −3,

2.7. ∫ f (x)dx ,

−3 < x ≤1,

f (x) = 2, если

−5

если

x >1.

3. Вычислите несобственные интегралы (или установите их расходимость):

3.1. ∞∫ln xdx		;	3.2. ∫0	x e−4 x2 dx ;
1	x		−∞

4. Вычислите площади фигур, ограниченных графиками функций:

4.1.y = 2x2 − x +2,

y = 0, x = 3, x = 0.

5.Найдите среднее значение функций:

5.1.y =sin x, π4;π2 ;

4.2.y = x ,

y = 0, x =1, x = 2.

5.2.y = 2 +3x,[0;3].

6. Решите уравнение ∫x (1 −2t)dt =1.

7. Найдите модуль и аргумент комплексного числа z = − 3 +3i . Постройте это число на комплексной плоскости.

Вариант № 20

1. Найдите неопределённые интегралы:

1.1. ∫

−

dx ;

1.5. ∫arctg 2xdx ;

1.2. ∫cos x (4 −3sin x)4 dx ;

1.6. ∫

;

exdx

+4x −3

1.3. ∫

;

1.7. ∫cos

x sin

xdx ;

cos2 ex

1.4. ∫x2 5 (4 −3x3 )2 dx ;

1.8. ∫sin( x 5) cos 2xdx .

2. Вычислите определённые интегралы:

2 ctg3 xdx

xdx

2.1. ∫

;

2.5. ∫

, замена

;

sin

+ x

1 1

2.2. ∫3

;

2.6. ∫3

3 − x2 dx , замена x =

3 sin t ;

2x +5

π4

ex ,

если

x ≤ −7,

2.3. ∫(3 −2x) cos 4xdx ;

если−7 < x ≤ −1,

2.7. ∫ f (x)dx , f (x) = x3 ,

−9

−4

, если

x > −1.

3. Вычислите несобственные интегралы (или установите их расходимость):

∞	xdx					0	−x
3.1. ∫					;	3.2. ∫	3	dx ;
3.1. ∫	(1− x	2	)	3	;	3.2. ∫	3	dx ;
2	(1− x		)			−∞

4. Вычислите площади фигур, ограниченных графиками функций:

4.1.y =5 − 2x2 ,

y =3x2.

5.Найдите среднее значение функций:

5.1.y = x x,[1;9];

6. Решите уравнение ∫x (2t +1)dt = 0 .

4.2.y = x3 ,

y =8, x = 0.

5.2.	y =	ln2 x	,[1;e].
		x

7. Найдите модуль и аргумент комплексного числа z =3 − 3i . Постройте это число на комплексной плоскости.

4.2.4. Решение типового варианта и образец оформления индивидуального задания № 2

Вариант № 0 1. Найдите неопределённые интегралы:

∫

ln xdx ;

1.1.

−

−7

−

dx ;

1.5.

1.2. ∫5 6 − 2xdx ;

1.6. ∫

;

x2 −6x + 25

1.3. ∫

;

1.7. ∫cos

3xdx ;

xln2 x

1.4. ∫sin 2x 3 2 −3cos 2xdx ;

1.8. ∫sin

cos3xdx ;

Решение

∫

1.1.

−

−7

−

Интеграл вычисляется непосредственным интегрированием. При этом используются свойства линейности неопределённого интеграла.

4 x

∫

−

−7 −

= ∫

dx −

∫

dx − ∫7dx − ∫

dx =

∫x3dx −4∫x−2dx −7∫dx −

∫x 14 dx =

−4

x−1

−7x −

x54

+C =

−1

+4x−1 −7x −

x5 4

+C.

Интегралы 1.2, 1.3 и 1.4 вычисляются подведением под знак дифференциала.

1.2. ∫5 6 − 2xdx

∫5 6 −2xdx = ∫(6 − 2x) 15 dx = ∫(6 −2x) 15 d(6 −2x) = −2

= −	1	∫(6 −2x)15 d (6 −2x) =−	1	(6 −2x)65		+C = −		5	(6 −2x)65 +C.
	2		2	6	5		12

1.3. ∫

xln2 x

(ln x)−2

(ln x)−1

∫

= ∫

d (ln x)

= ∫(ln x)

−2

d (ln x) =

+C .

x ln2 x

−1

1.4. ∫sin 2x 3 2 −3cos 2xdx

∫sin 2x 3 2 −3cos 2xdx = ∫sin 2x (2 −3cos 2x) 13 dx =

d (2 −3cos 2x)

= ∫sin 2x (2 −3cos 2x)

∫(2

−3cos 2x)

d(2 −3cos 2x) =

(2 −3cos 2x)4 3

6sin 2x

+C =

(2 −3cos 2x)4 3 +C.

1.5. ∫

x3 ln xdx

Интеграл вычисляется с помощью формулы интегрирования по частям ∫udv = uv − ∫vdu .

u = ln x du = 1 dx

∫

x3 ln xdx = ∫x

2 ln xdx =

dv = x3 2 dx v = ∫x

3 2 dx =

x5 2

x52

5 2

− ∫

∫x

= ln x

dx =

ln x −

2 dx

x5 2

x52 ln x −

+C =

5 2 ln x −

x52 +C.

1.6. ∫

x2 −6x + 25

Интеграл содержит квадратный трехчлен. Преобразуем выражение,

стоящее в знаменателе подынтегральной дроби

x2 −6x +25 = x2 −2 3 x +32 −32 +25 = (x −3)2 +16 .

∫

= ∫

∫

d (x −3)

arctg

x −3

+C.

x2 −6x +25

(x −3)2 +16

(x −3)2 +42

Интегралы 1.7 и 1.8 содержат тригонометрические функции

1.7. ∫cos3 3xdx

∫cos3 3xdx = ∫cos2 3x cos3xdx = ∫(1−sin2 3x)cos3xdx =

=∫(cos3x −sin2 3x cos3x)dx = ∫cos3xdx − ∫sin2 3x cos3xdx =

=∫cos3x d (33x) − ∫sin2 3x cos3x d3cos3(sin 3xx) =13 ∫cos3xd (3x) −

−1 ∫sin2 3xd (sin 3x) =1 sin 3x − 1 sin3 3x +C. 3 3 3 3

1.8. ∫sin 2x cos 3xdx

Для преобразования подынтегрального выражения воспользуемся формулой тригонометрии sin α cosβ = 12 (sin(α+β) +sin(α−β)) .

sin

cos 3xdx =

sin

3x +

+sin

3x −

sin

dx +

∫

2 ∫

∫

∫sin

d (3,5x)

∫sin

d (2,5x)

3,5

2,5

∫

sin

= −

cos

−

cos

+C .

2. Вычислите определённые интегралы:

4 tg2 xdx

xdx

2.1. ∫0

;

2.4. ∫0

, замена x =t

−1;

cos2 x

3 1 + x

xdx

2.2. ∫

;

2.5. ∫

25 − x

dx , замена x =5sin t ;

1 2x

x ≤ 0,

π3

−3,

если

2.3. ∫(4 −3x)sin 3xdx ;

2.6. ∫ f (x)dx ,

f (x) =

если

0 < x ≤1,

−3

x −4,

если

x >1.

Решение

π/ 4 tg2 xdx

2.1.

∫0

cos2 x

π4

∫

tg xdx

= ∫

cos2 x

cos

2 x

tg3 π − tg3 0 =

xdx

2.2. ∫1

2x2 +5

xdx

∫

2x2 +5

2x2


d (tg x)					π		4				tg3 x	π4
							4
				=	∫tg				2	x d (tg x) =		=
1				=	∫tg					x d (tg x) =	3	=
cos2 x					0							0
cos2 x					0							0
3		3			1
(1	−0		) =					.
(1	−0		) =			3		.

d (2x2 +5)		1	3	d (2x2 +5) 1							3
			3						2
			∫					2x	2
	=				=		ln			+5	=
4x	=	4		2x2 +5	=	4	ln			+5	=
4x		4		2x2 +5		4
			1								1

= 14 (ln(2 32 +5) −ln(2 12 +5))= 14 (ln 23 −ln 7).

π3

2.3.∫(4 −3x)sin 3xdx

Интеграл вычисляется методом интегрирования по частям

	b	b
	∫udv = uv	ba − ∫vdu .


	a	a
π	3		u = 4 −3x du = −3dx
π	3		u = 4 −3x du = −3dx
∫(4 −3x)sin 3xdx =			dv =sin 3xdx v = ∫sin 3x	d (3x)	= −	1	cos3x	=
0			dv =sin 3xdx v = ∫sin 3x	3	= −	3	cos3x
				3		3

π3

(4 −3x)

−

cos3x

−

cos3x

∫0

= −

((4 −π) cos π−4cos0)− ∫3 cos3x

−

(sin π−sin 0) =

8 −π

(−3dx) =

d (3x)		1				1		π
	= −		(−4	+ π−4)	−		sin 3x	3	=

3		3				3		0

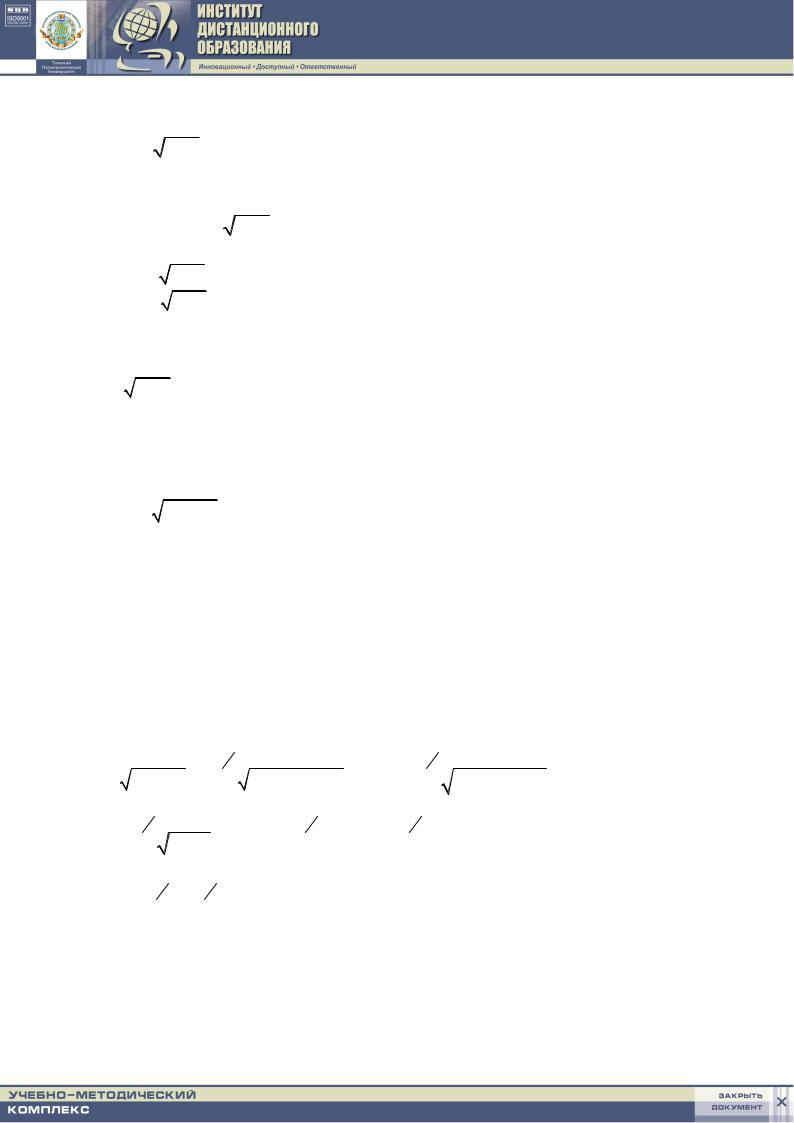
2.4. ∫7	xdx	, замена x =t3 −1
2.4. ∫7	3	, замена x =t3 −1
0	1 + x

Выполним замену в интеграле по формуле x = t3 −1. Тогда dx = 3t2dt ;

t3 = x +1 t = 3 x +1 .

Находим новые пределы интегрирования

tнижн = 3 0 +1 =1, tверхн = 3 7 +1 = 2.

Тогда

7	xdx					2		(t			3	−			2		dt	2													2							t	5		t	2	2
7						2					3				2			2													2								5			2	2
∫					=	∫							1) 3t					= 3			(t3			−1)tdt = 3								(t4 −t)dt = 3								−			=
	3 1+ x				=									t				= 3			(t3			−1)tdt = 3								(t4 −t)dt = 3								−			=
	3 1+ x													t						∫										∫								5 2					1
0						1												1													1												1
		25			22					1			1						32 −1				1−4								47				141		.
=	3		−				−					+			= 3							+					= 3							=
=	3	5	−		2		−			5		+	2		= 3			5				+					= 3				10			=	10
		5			2					5			2					5							2						10				10
2.5. ∫5			25 − x2 dx , замена x =5sin t
	0
		Выполняем замену																										x
		x =5sin t dx = 5cos tdt; t = arcsin																										x		.
		x =5sin t dx = 5cos tdt; t = arcsin																												.
																											5
		Находим новые пределы интегрирования
tнижн		= arcsin							0		= 0,
tнижн		= arcsin						5			= 0,
tверхн		= arcsin						5			= arcsin1 = π.
		Тогда						5										2
		Тогда									π																		π
5											π																		π
5	25 − x2 dx = ∫2													25 −25sin2 t 5costdt =∫2
∫	25 − x2 dx = ∫2													25 −25sin2 t 5costdt =∫2																		25(1−sin2 t) 5costdt =
0											0																0
	π																		π								π
= 25 ∫2				cos2 t costdt = 25 ∫2 cos2 tdt =25 ∫2																									1+cos 2t							dt =
= 25 ∫2				cos2 t costdt = 25 ∫2 cos2 tdt =25 ∫2																																dt =
		0																0									0					2
	25	π	2				π2									d (2t)					25					1							π
	25	π	2				π2									d (2t)					25					1							2
=				dt +					∫		cos 2t									=			t +				sin 2t							=
=	2			dt +							cos 2t						2			=		2	t +			2	sin 2t							=
	2	∫															2					2				2
		0						0																									0
		0						0																									0

	25			π		1						1											25π
=					+			sin π−0 −							sin 0						=					.
=	2				+	2		sin π−0 −				2			sin 0						=			4		.
	2			2		2						2												4
																							если						x ≤ 0,
				4									−3,										если						x ≤ 0,
2.6. ∫ f (x)dx ,										f (x) =								x,					если						0 < x ≤1,
2.6. ∫ f (x)dx ,										f (x) =								x,					если						0 < x ≤1,
			−3												2			x −4,						если					x >1.
															2

													3
				Воспользуемся свойством аддитивности определённого интеграла
				4						0									1										4
				∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx + ∫ f (x)dx .
				−3						−3									0										1
4				Тогда			0					1										4												0					1
4							0					1										4		2x										0					1	1
∫							∫					∫										∫			3								∫						∫
		f (x)dx =							(−3)dx +									xdx +										−4 dx = −3							dx +					x 2dx +
−3							−3					0										1										−3							0
	2		4				4				0						x32			1		2 x2					4			4
																				1

			∫	xdx −4			∫		dx =−3x																				−4x
+	3		∫				∫				−3			+			3				+	3			2					1	=
+			1				1							+					2	0	+						1				=



									2					1																		2				15					40
= −3(0 +3) +									2	(1 −0) +				1		(16 −1) −4(4 −1) = −9 +																2		+		15		−12 = −			40	.
= −3(0 +3) +									3	(1 −0) +				3		(16 −1) −4(4 −1) = −9 +																3		+			3	−12 = −			3	.
									3					3																		3					3				3

3. Вычислите несобственные интегралы (или установите их расходимость):

3.1. ∫∞

;

3.2.

∫1

e−2 xdx .

(x +5)4

−4

−∞

Решение

3.1. ∫∞

(x +5)4

−4

∞

−4

+5)−3

∫

= lim

∫

(x +5)

d(x +5)

= lim

(x +5)4

−3

b→∞

−4

(x +5)−3

= lim

= −

lim

−1 =

−3

−4

(b +

b→∞

Так как предел существует и конечен, то несобственный интеграл сходится.

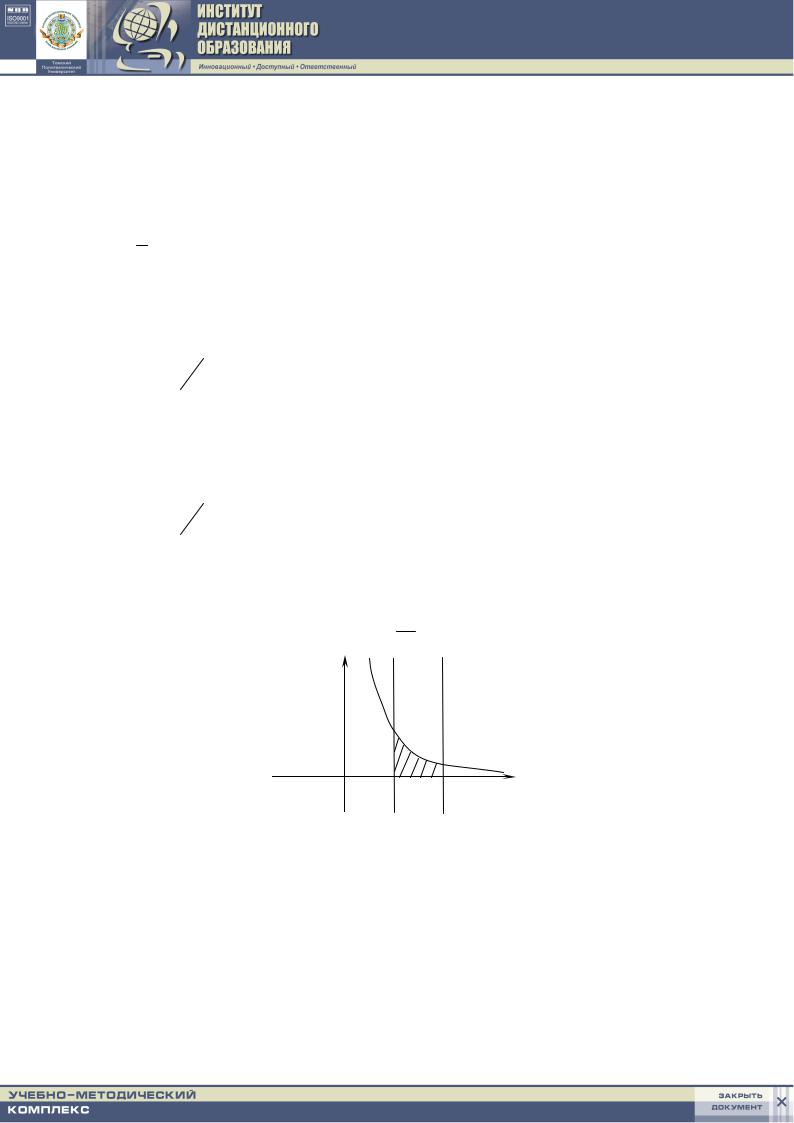
3.2. ∫1		e−2 xdx
	−∞					1 alim→−∞(e−2 x	1a )=
∫1	e−2 xdx = alim→−∞ ∫1 e−2 xdx =alim→−∞ ∫1 e−2 x d (−2x)				=−
					=−

−∞		a	a	−2		2

=− 1 lim (e−2 −e−2a )= ∞.

2 a→−∞

Так как предел равен бесконечности, то несобственный интеграл расходится.

4. Вычислите площадь фигуры, ограниченной графиками функций:

	y = 1	x	2 ,
		x			2
4.1.			4.2.
4.1.	y = 0		4.2.	y = 2x − x ,
	x =1,			y = 0.

	x = 2.
			Решение
	y = 1	x	2 ,
		x
4.1.
4.1.	y = 0
	x =1,

x = 2.

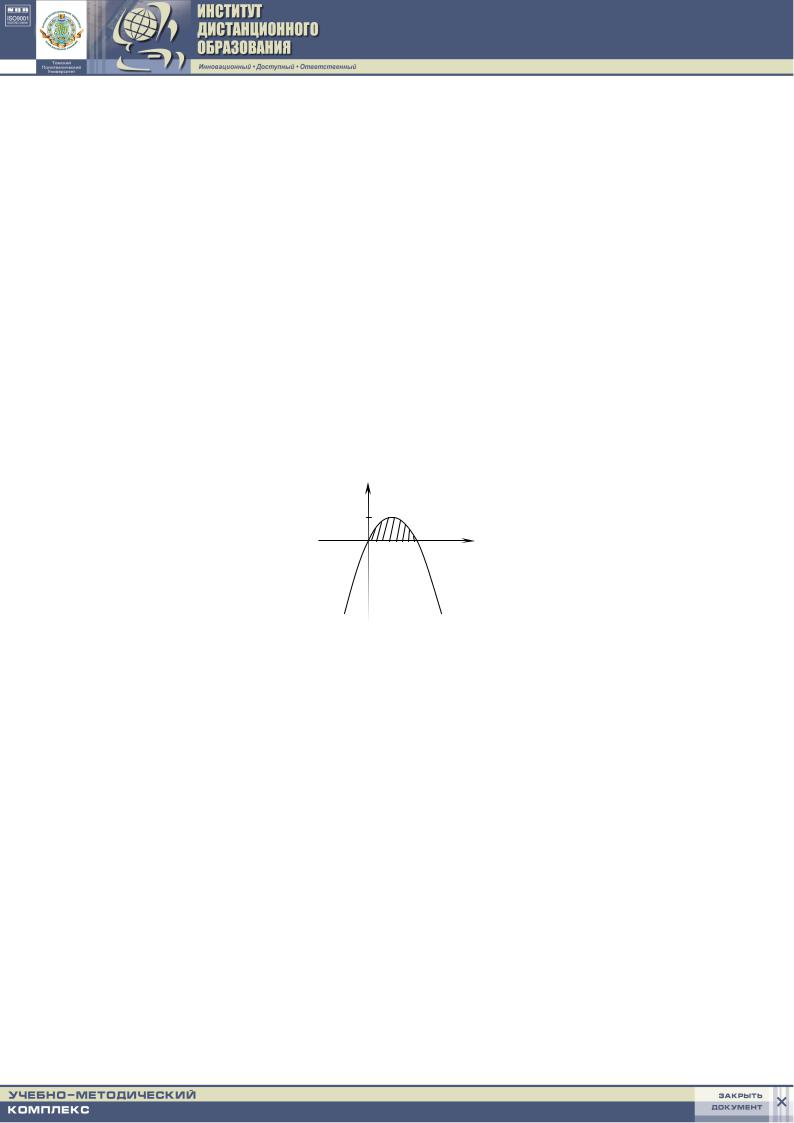
Построим график функции y = x12 и прямые x =1, x = 2. y

Так как фигура, площадь которой надо найти, снизу ограничена осью Ox , то формула для вычисления площади имеет вид

S = ∫b	f (x)dx , где	f (x) =	1	, a =1,b = 2.
			2
a			x

Окончательно получаем

S =	2	dx			1	2		1			1

				= −			= −		−1	=		(кв. ед.).
	∫x		2		x			2			2
						1
	1

4.2.y = 2x − x2 ,y = 0.

Построим фигуру, ограниченную линиями y = 2x − x2 и y = 0. Графиком функции y = 2x − x2 является парабола, ветви которой направле-

ны вниз. Найдём вершину параболы

xв = −2ab = −−22 =1, yв = y(xв) = 2 1−12 =1.

Находим абсциссы точек пересечения параболы y = 2x − x2 с осью Ox , для этого решим уравнение

2x − x2 = 0 x(2 − x) = 0 x = 0, x = 2.

Графиком функции y = 0 является ось Ox .

0 2

Найдём площадь фигуры по формуле
S = ∫b	f (x)dx , где					f (x) = 2x − x2 ,a = 0,b = 2.
a
2							x3	2		8		4
								2

S = ∫(2x − x		2			2
			)dx = x			−			= 4 −		−(0 −0) =		(кв.ед.).
			)dx = x			−	3		= 4 −	3	−(0 −0) =	3	(кв.ед.).
0							3	0		3		3
0								0			f (x) на отрезке [a;b]:
5. Найдите среднее значение функции											f (x) на отрезке [a;b]:
5.1. f (x) = 3x ,				[−1; 2];							5.2. f (x) = x2 −2x, [0; 4].

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.05.2015141.18 Кб95Modul_4.docx
#
17.09.2019692.24 Кб67Moya_rabota_po_gosam.docx
#
21.12.20183.36 Mб79MO_shpor.doc
#
23.12.2018483.33 Кб40Msis.doc
#
29.05.20151.02 Mб60mu.pdf
#
29.05.20151.72 Mб12mu.pdf
#
29.05.20151.99 Mб72mu.pdf
#
29.05.20151.64 Mб12mu.pdf
#
29.05.201534.55 Mб18mu.pdf
#
10.11.20183.99 Mб1MultimediaMetod.doc
#
18.11.20191.99 Mб39MU_Adsorbtsia_Lengmyura.doc