Вопрос 14.

Для количественного рассмотрения влияния температур вводят понятие температурного эффекта реактивности и температурного коэффициента реактивности.

Температурный эффект реактивности (ТЭР) – интегральная характеристика влияния T на  и представляет собой изменение  при разогреве или расхолаживании реактора в заданном интервале температур от T₁ до T₂. Изменяется в относительных единицах или процентах:

(1)

Обычно подразумевается изменение  при разогреве от 20⁰С до рабочей температуры.

Температурный коэффициент реактивности (ТКР) – дифференциальная характеристика влияния T на  и представляет собой изменение  при изменении температура реактора на 1⁰С. Измеряется ТКР в ⁰С^–1 и обозначается .

, ⁰C^–1. (2)

Так как , то

(3)

Когда k_эф1 для практических приложений часто используется удобная зависимость

(4)

ТЭР и ТКР связаны между собой соотношением:

(5).

Таким образом, мы будем в основном рассматривать температурный коэффициент реактивности, который определяет и температурный эффект реактивности.

Для удобства теоретического анализа температурный коэффициент реактивности обычно разделяют на три части:

• ядерный температурный коэффициент (ЯТКР), обусловленный влиянием температуры на эффективные сечения взаимодействия,

• плотностной температурный коэффициент (ПТКР), связанный с изменением плотности материалов активной зоны,

• геометрический температурный коэффициент реактивности, зависящий от изменения формы и размеров твердых материалов активной зоны.

Вопрос 15

Рассмотрим два случая

1. Пусть мало по сравнению с(). Тогда. Раскладывая квадратный корень в выражении (4) в ряд Маклорена (при) и ограничиваясь первым значащим слагаемым, выражение (4) примет вид:

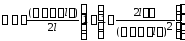(7)

Таким образом, в рассматриваемом случае решениями уравнения (7) являются:

(8)

, вследствие малости третьего слагаемого в квадратных скобках им пренебрежем, тогда окончательно имеем:

(9)

Для однозначного определения потока нейтронов согласно выражению (5) [] необходимо определить коэффициентыА₀ и А₁.

Запишем уравнение баланса для концентрации ядер-предшественников:

(10)

С другой стороны согласно выражению (6) -

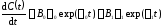(11)

Сравнивая (10) и (11) и учитывая (5) и (6) получаем:

Разделяем слагаемые, содержащие константы типа А и типа В.

Равенство сумм предполагает равенство соответствующих слагаемых:

(12)

(13)

Подставим в выражения (12) и (13) значения 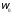ив соответствии с соотношениями (8) и (9):

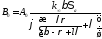. Оценив порядок величин (), пренебрежем произведением. Тогда

(14)

(15)

В (15) аналогично (14) пренебрегли произведением вследствие его малости.

В соответствие с (5) и (6) запишем начальные условия: Ф(0)=А₀+А₁=Ф₀ и С(0)=В₀+В₁=С₀. С другой стороны в соответствие с (10) для момента времени t=0 получим:

(16)

Рассматривая совместно начальные условия и выражения (14)-(16), проведем преобразования:

(17)

Выразим из начальных условий А₁=Ф₀–А₀ и подставим в (17):

. В дроби порядок числителя составляет 10^-6, а порядок знаменателя 10^-3. Таким образом, вся дробь стремиться к 0. Тогда: (18)

Выразим из начальных условий А₀=Ф₀–А₁ и подставим в (17):

. Также, как и в случае А₀, вследствие малости дроби во втором слагаемом получаем:

(19)

Таким образом, закон изменения нейтронного потока во времени примет вид:

(20)

Нейтронный поток представляется разностью двух слагаемых, из которых один с течением времени растет, в другой – падает. Рассмотрим конкретный пример. Предположим, что l = 10^-3 c, =0,0064,=0,077 с^-1 (случай деления 235U), введенная реактивность составляет =0,003. Тогда соотношение (20) можно представить в следующем виде:

Ф(t)/Ф(0) = 1,88 exp(0.07t) – 0,88 exp(-3,4t) (21)

На рисунке приведен график изменения во времени как всего соотношения (21), так и отдельных его слагаемых. Несложно убедиться, что в первый момент времени после скачка реактивности (около 0,2 с) изменение потока нейтронов почти полностью определяется вторым (переходным) слагаемым. Можно оценить период реактора в этом случае. Для этого нужно известное выражение Ф(t)=Ф₀exp(t/T) и соотношение (20) продифференцировать по времени и рассмотреть времена, близкие к нулю (t=0). Тогда получим:

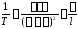или (22)

При малых значениях реактивности () первое слагаемое в выражении (22) много меньше, чем второе. Следовательно,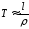. Это означает, что при малых значениях положительной реактивности запаздывающие нейтроны практически не участвуют в изменении потока нейтронов в начальный момент времени после скачка реактивности. По истечении времени, равного примерно 1 с второе (переходное) слагаемое в выражениях (20) и (21) затухает, и поток нейтронов изменяется по закону:

отсюда период реактора равен , что соответствует установившемуся режиму разгона реактора при малых положительных значениях скачка реактивности. Таким образом, поведение реактора в этом случае определяется поведением запаздывающих нейтронов. Если вернуться к рассмотренному примеру, то установившийся период составит величину около 15 с, когда как в отсутствии запаздывающих нейтронов он равен примерно 0,4 с. Отсюда можно констатировать, что наличие запаздывающих нейтронов уменьшает скорость увеличения потока нейтронов при скачке положительной реактивности.

Необходимо отметить одну важную особенность – резкий рост (практически скачком) потока нейтронов в переходном режиме разгона реактора (первое время после скачка реактивности) и относительно слабый – в установившемся.

2. Рассмотрим второй случай положительной реактивности. Пусть введенная положительная реактивность велика по сравнению с (). Тогда общее решение квадратного уравнения (3), которое имеет вид (4):

может быть переписано следующим образом (с учетом малости величины ):

(23)

Раскладывая, как и в случае малых , квадратный корень в выражении (23) в ряд Маклорена и ограничиваясь первым значащим слагаемым, выражение (23) примет вид:

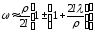(24)

Таким образом, в случае больших значений реактивности корнями уравнения (3) являются:

(25)

В (25) отношение по порядку величины много больше, чем.

(26)

Сравнивая (25) и (26), видно, что . Следовательно, нет необходимости определять константы в законе изменения потока нейтронов во времени, т.к. в любой сколь угодно малый момент времени поток практически полностью определяется первым слагаемым:(переходный режим разгона практически отсутствует). Другими словами поток нейтронов будет изменяться с периодом , т.е. запаздывающие нейтроны практически не принимают участия в изменении потока нейтронов.

На рис. 2 проиллюстрированы вышеуказанные выводы. Видно, что при малых изменение потока нейтронов во времени имеет «изломы», соответствующие наличию переходных режимов, при большихизменение потока происходи почти по прямой, что говорит о незначительных переходных режимах разгона.

Дадим физическую интерпретацию полученных результатов. (См. вопрос 11)

В нашем анализе мы сравнивали величину введенной положительной реактивности с величиной доли запаздывающих нейтронов. Можно предположить, что является некой мерой возможности управления реактором. Для доказательства этого введем понятие мгновенно критического реактора. Мгновенная критичность – это состояние реактора, при котором он становится критическим на одних мгновенных нейтронах. Получим условие мгновенной критичности. Для этого воспользуемся известным уравнением диффузии с учетом запаздывающих нейтронов:

Т.к. мы договорились вести речь о реакторе на мгновенных нейтронах, то третье слагаемое, описывающее источник запаздывающих нейтронов, можно исключить. При этом в реакторе, находящемся в критическом состоянии, поток не должен изменяться во времени, так что производная =0. Следовательно, записанное уравнение диффузии примет вид (раскрывая все скобки):

(27)

Разделим обе части (27) на , вспомним, чтои получим условие:

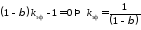(28)

Из определения реактивности следует, что. Подставив это в (28) получим условие, при котором реактор будет мгновенно критическим:

(29)

Соответственно, при реактор будет надкритическим на мгновенных и запаздывающих нейтронах, а при- только на мгновенных. Например, реактор на тепловых нейтронах, в котором делящимся материалом является²³⁵U, достигает мгновенной критичности при величине реактивности, равной 0,0064. Если введенная реактивности превысит эту величину, то нейтронный поток начнет нарастать с большой скоростью, определяемой мгновенными нейтронами, и реактор вскоре выйдет из-под контроля. При скачке реактивности величиной, меньшей 0,0064, управление реактором становится возможным благодаря эффекту запаздывающих нейтронов, хотя период реактора будет уменьшаться по мере того, как приближается к, т.е. для нашего примера к величине 0,0064.