Математика РГР

2) Для потенциального поля вектор поля V gradU , где U – потенци-

ал поля, то есть

Из условия U (0;0;0) 30 находим С:

30 0 0 0 C,

C30

ипотенциал поля равен

U(x; y; z) y2 xz 2 yz 2 30.

3)Работа потенциального поля между точками M1 и M 2 равна разно-

сти значений потенциала в конечной и начальной точках.

Проверили еще один признак потенциального поля: циркуляция потен-

циального поля V вдоль любого замкнутого контура равна нулю.

111

Ответ: 1. rotV 0 ,

2.U (x; y; z) y2 xz 2 yz 2 30,

3.AM1M 2 0, AM 2 M 3 1, AM 3 M1 1, Ц 0.

22.Найти вероятность безотказной работы участка цепи, если известно, что

каждый i -ый элемент работает независимо от других с вероятностью pi ( i

= 1, 2, 3, 4, 5, 6).

p1 0,6, p2 0,7, p3 0,8, p4 0,5, p5 0,9, р6 0,7 .

Рисунок 19 – Электрическая схема

Решение. Участок цепи будет работать безотказно, если работают бло-

ки 1–2 и 3–4–5–6 (последовательное соединение).

Рассмотрим блок 1–2. Элементы 1 и 2 соединены параллельно, следо-

вательно, блок 1–2 будет работать, если хотя бы один из элементов 1, 2 ис-

правен.

Р1 2 1 (1 р1 )(1 р2 ) 1 0,4 0,3 0,88 – надежность блока 1–2.

Рассмотрим блок 3–4–5–6. Блок 3–4–5–6 будет безотказно работать хо-

тя бы в одном из случаев:

исправны элементы 3 и 4,

исправен элемент 5,

исправен элемент 6.

Р3 4 р3 р4 0,8 0,5 0,4 – вероятность безотказной работы блока

112

3–4.

Р3 4 5 6 1 (1 р3 4 )(1 р5 )(1 р6 ) 1 (1 0,4)(1 0,9)(1 0,7) 0,982 –

надежность блока 3–4–5–6.

Следовательно, Р Р1 2 Р3 4 5 6 0,88 0,982 0,864 – искомая надежность участка

цепи.

23. Рабочий обслуживает четыре однотипных станка. Вероятность того, что любой станок в течение часа потребует внимания рабочего, равна 0,6. Пред-

полагая, что неполадки на станке независимы, найти вероятность того, что в течение часа потребуют внимания рабочего: 1) все четыре станка; 2) ни один станок; 3) по крайней мере один станок.

Решение. Обозначим через А1, А2 , А3 , А4 события, состоящие в том, что в течение часа потребуют внимания рабочего соответственно первый, вто-

рой, третий, четвертый станки. По теореме умножения вероятностей незави-

симых событий вероятность того, что в течение часа все станки потребуют внимания рабочего, то есть произойдут события и А1 , и А2 , и А3 , и А4 , вы-

числим по формуле

Р А1 А2 А3 А4 Р А1 Р А2 Р А3 Р А4 0,6 0,6 0,6 0,6 0,1296.

Вероятность того, что в течение часа станок (любой) не потребует вни-

мания рабочего, найдем по правилу вычисления вероятности противополож-

ного события:

Р А1 Р А2 Р А3 Р А4 1 0,6 0,4.

Следовательно, вероятность события В, состоящего в том, что ни один станок в течение часа не потребует внимания рабочего, то есть произойдут события и А1 , и А2 , и А3 , и А4 , равна

Р(В) Р А1 А2 А3 А4 Р А1 Р А2 Р А3 Р А4 0,4 0,4 0,4 0,4 0,0256 .

113

Событие, состоящее в том, что в течение часа по крайней мере один из четырех станков потребует внимания рабочего, и событие В являются противоположными. Поскольку Р(В) 0,0256 , то

Р(В) 1 Р(В) 1 0,0256 0,9744 .

24. Заданы законы распределения двух независимых случайных величин Х и

У

Найти математическое ожидание и дисперсию для случайной величины

Z 2X 7Y .

Решение. Найдем математические ожидания и дисперсии случайных величин Х и У:

М( Х ) 5 0,4 2 0,3 3 0,1 4 0,2 0,3,

М(У ) 1 0,2 8 0,8 3,4.

Напишем законы распределения для случайных величин Х 2 и У 2 :

Найдем математические ожидания для случайных величин Х 2 и У 2 :

М( Х 2 ) 25 0,4 4 0,3 9 0,1 16 0,2 15,3,

М(У 2 ) 1 0,2 16 0,8 13,0.

Отсюда

D( X ) M ( X 2 ) M ( X ) 2 15,3 ( 0,3)2 15,21, D( X ) M (Y 2 ) M (Y ) 2 13,0 3,42 1,44.

114

Пользуясь свойствами математического ожидания и дисперсии, а также независимостью случайных величин Х и У, получаем

M (Z ) M (2X 7Y ) 2M ( X ) 7M (Y ) 2 ( 0,3) 7 3,4 24,4, D(Z ) D(2X 7Y ) 4D( X ) 49D(Y ) 4 15,21 49 1,44 131,4.

25. Станок-автомат изготавливает шарики. Шарик считается годным, если отклонение Х его диаметра от проектного размера по абсолютной величине меньше 0,9 мм. Считая, что случайная величина Х распределена нормально с нулевым математическим ожиданием и со средним квадратическим отклоне-

нием 0,5 мм, найти, сколько процентов годных шариков изготовляет

станок-автомат.

Решение. Воспользуемся формулой для вычисления вероятности за-

данного отклонения нормально распределенной случайной величины Х от ее

математического ожидания

115

Выполнить статистическую обработку результатов измерений по следующе-

му плану:

1)Построить статистическое распределение выборки.

2)Выполнить точечные оценки среднего значения x и дисперсии D X

случайной величины X .

3)Построить гистограмму относительных частот, установив статистиче-

ский (эмпирический закон распределения).

4)На том же чертеже построить кривую нормального распределения с параметрами a x и D X и проанализировать, хорошо ли стати-

стические данные описываются нормальным законом распределения.

Решение. 1) Построение статистического распределения выборки.

Данную выборку преобразуем в вариационный (интервальный ряд).

Для этого диапазон изменения случайной величины X в выборке делим на k

интервалов. Число интервалов k определяется по эмпирической формуле с округлением до ближайшего целого. В нашем случае объем выборки n 60 , поэтому k 1 3, 2lg 60 6, 69 7 . Ширину каждого интервала

наименьший элементы выборки. Величина должна выбираться с точно-

стью выборки и округляться в сторону завышения.

Границы интервалов вычисляются по формулам

x0* xmin

xi* 1 xi* i 0,1, 2,...k 1

Для каждого интервала i подсчитываем количество попавших в него элемен-

тов ni . Если элемент совпадает с границей двух соседних интервалов, то его следует отнести к интервалу с меньшим номером.

116

На основании полученных результатов заполняем первые четыре столбца таблицы 4.

Таблица 4 – Характеристики интервального ряда

X .

Математическое ожидание можно оценить, взяв среднее арифметиче-

ское чисел из таблицы 3:

x x1 x2 ...xn . n

Исправленная дисперсия может быть вычислена по формуле

Эти формулы целесообразно использовать, если объем выборки неве-

лик, или все статистические данные внесены в компьютер (например, в про-

грамму Excel). При выполнении расчетов вручную используется иная мето-

дика, которая требует меньших вычислений.

В случае выборки большого объема среднее значение случайной вели-

чины X удобно вычислить по формуле

117

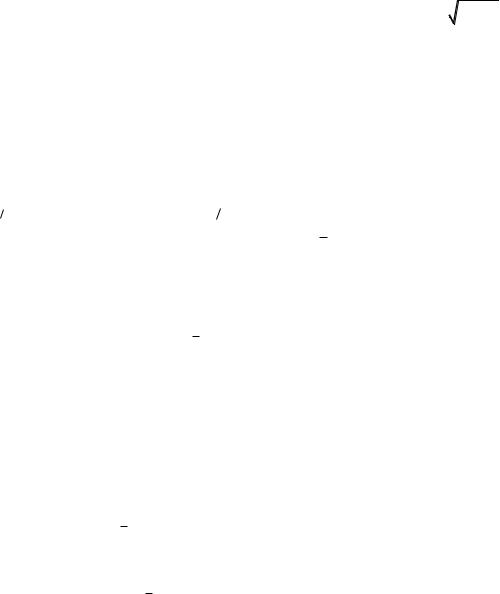
Для дисперсии получаются формулы следующего вида:

При таком выборе формулы перехода величины ui будут принимать после-

довательные целые значения, близкие к нулю.

Пользуясь свойствами дисперсии и математического ожидания, можно получить формулы, выражающие x и D X через соответствующие характе-

ристики случайной величины U , аналогичные формулам (1,2).

Таким образом, при решении пункта 3 настоящей задачи будем действо-

вать в следующем порядке

2.В нашем случае c x4 67, 78 .

3.В 6 столбец таблицы 4 заносим числа –3, –2, –1, 0, 1, 2, 3, которые по-

лучаются из значений xi по формуле (3).

118

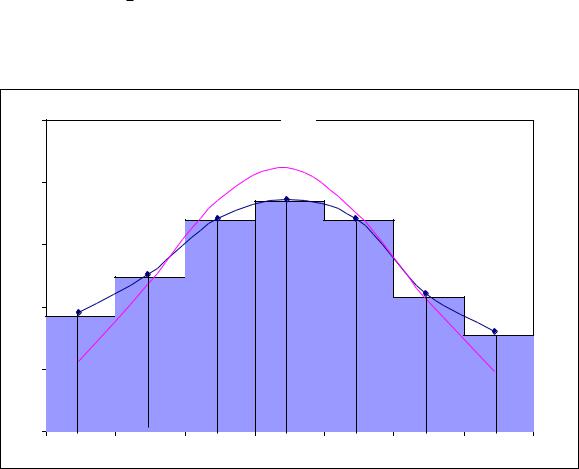
3) Построение гистограммы относительных частот.

Гистограммой называется ступенчатая фигура, состоящая из прямо-

угольников, основаниями которых служат частичные интервалы длиной , а

высоты равны Wi .

Высоты прямоугольников записываем в 7 столбец таблицы 4. Диа-

грамма, построенная по данным таблицы 4, показана на рисунке 21.

Если теперь середины верхних сторон прямоугольников соединить плавной линией, то эта линия будет аналогом плотности распределения слу-

чайной величины – эмпирическим законом распределения.

4) Сравнение эмпирического и теоретического законов распределения

случайной величины X.

Из вида кривой эмпирического распределения следует, что случайная

величина X должна иметь закон распределения, близкий к нормальному.

Для сравнения в той же системе координат построим кривую нормального закона распределения

дущем пункте. Таким образом, 1,89 .

Одним из критериев, позволяющих установить справедливость нор-

мального закона распределения случайной величины X, является правило трех сигм. В случае нормально распределенной величины вероятность от-

клонений от x больше, чем на величину 3 , мала, следовательно, такие от-

119

клонения встречаются крайне редко. Для наших статистических данных

3 5, 67 . Из графика и таблицы можно сделать вывод, что величина X редко отклоняется от x более, чем на 3 , следовательно, ее закон распределения близок к нормальному.

27. В задаче приведены данные по группе хозяйств о дозах внесения удобре-

ний на 1 га посева зерновых в ц. (Х) и об урожайности зерновых культур в ц.

с 1 га. (Y). Методом корреляционного анализа нужно исследовать зависи-

мость меду этими признаками, построить корреляционное уравнение (урав-

нение регрессии), рассчитать коэффициент корреляции и построить график корреляционной зависимости. Сформулируем выводы корреляционного ана-

лиза.

Решение. Для решения следует составить вспомогательную таблицу.

Вспомогательная таблица для расчета коэффициентов регрессии и кор-

реляции

120