Математика РГР

х (t) pX ( p) x(0) pX ( p) 1,

y (t) pY ( p) y(0) pY ( p) 1.

Следовательно, операторная (изображающая) система имеет вид:

pX ( p) 1 3X ( p) 4Y ( p) 0,pY ( p) 1 4X ( p) 3Y ( p) 0.

Представим дробь в виде суммы простых дробей:

91

t ( 3;3) .

Выясним вопрос о сходимости этого ряда на концах интервала.

При t 3 ряд принимает вид

92

Получили числовой знакочередующийся ряд, применим к нему признак Лей-

бница:

Ответ: Область сходимости x 2;8 .

93

14. а) Найти разложение в степенной ряд по степеням х решения диф-

Из начальных условий уже известны y(0) и y (0) . Подставив эти значения в

заданное уравнение, вычислим y (0) :

y (0) 0 0 1 e0 0.

Последовательно дифференцируя данное уравнение, будем иметь:

y (x) y xy y e x xy e x ; y(IV ) (x) y xy e x .

Теперь вычислим значения производных при x 0 :

y (0) 1; y(IV ) 1.

Следовательно, y(x) 1 10! x 20! x2 31! x3 41! x4 ... или

y(x) 1 16 x3 241 x4 ...

есть искомое частное решение.

14. б) Используя разложение подынтегральной функции в степенной

94

Разложим подынтегральную функцию в степенной ряд. Для этого ис-

пользуем ряд

сти полученного ряда ( 1;1) , то будем интегрировать почленно в указанных пределах:

В полученном знакочередующемся ряде четвертый член по абсолют-

ному значению меньше 0,001. Следовательно, требуемая точность будет обеспечена, если учитывать только первые три члена ряда.

Найти:

1) экстремум функции z(x; y) ;

95

2)gradz в точке А(1; –2);

3)наибольшую скорость возрастания z(x; y) точке А(1; –2).

Решение. 1) Для отыскания экстремума функции z(x; y) предваритель-

но найдем частные производные первого и второго порядка:

Приравняем их к нулю и решим систему уравнений:

Решением системы является точка М(–4; 1). Точка М(–4; 1) называется подо-

зрительной на экстремум. Найдем частные производные второго порядка в точке М:

Из них составим определитель второго порядка

96

Так как 3 0 , то в точке М(–4; 1) есть экстремум. Производная

2 z 2 0 , а, значит, это точка минимума функции.

x2

zmin ( 4)2 ( 4) 1 12 9 ( 4) 6 1 20 1.

2) Градиент функции z найдем по формуле:

3) Наибольшая скорость возрастания функции равна модулю градиен-

та:

gradz( A) 132 ( 11)2 290 .

x2 y 2 2(z 4) находится в точке В(0; 0; 4), радиус окружности в плоско-

сти хОу равен 22 , осью цилиндра x2 y 2 4 является ось Оz, радиус по-

перечного сечения равен 2, а уравнение z 0 описывает координатную плос-

кость хОу.

97

Рисунок 12 – Декартова и цилиндрическая система координат точки М

Якобиан перехода от декартовых координат к цилиндрическим координатам

I .

Для вычисления объема тела в цилиндрической системе координат справедлива следующая формула:

V d d dz

V

или

В нашем случае (см. рис. 11) 0 2 , 0 2, а z находим из уравнения параболоида, учитывая цилиндрические координаты:

99

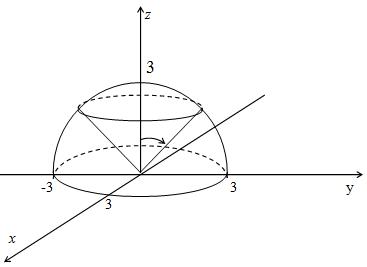
16. б) Найти объем тела, ограниченного сферой x2 y 2 z 2 9 и ко-

нусом x2 y 2 z 2 0 z 0 , через тройной интеграл, применяя сфериче-

скую систему координат.

Решение. Сделаем чертеж, учитывая, что центр сферы находится в начале координат (0; 0; 0), радиус равен 3; осью вращения конуса является

Рисунок 13 – Построение данного тела

С учетом характера области интегрирования V вычисления удобно вести в цилиндрических координатах ; ; r .

Зависимость между декартовыми и цилиндрическими координатами точки имеет вид:

x r cos sin ,y r sin sin ,

z r cos ,

100