1.1.5. Расчет и построение потенциальной диаграммы

Для расчета потенциалов в точках соединения элементов контура предварительно выбирают точку, потенциал которой принимают равным нулю, В качестве такой может быть взята любая точка заданного контура. Потенциал в каждой последующей точке зависит от того, какой элемент включен на расчетном участке. Потенциал в конце участка, содержащего источник напряжения, зависит от направления э.д.с. Если э.д.с. действует в направлении обхода контура, то потенциал в конце участка равен:

где – потенциал в начале участка.

Если действие э.д.с. и направление обхода контура не совпадают, то

Потенциал в конце участка с сопротивлением R зависит от направления тока. Если ток направлен от узла 1 к узлу 2, то потенциал в конце участка равен:

если наоборот, то

Для наглядной иллюстрации распределения потенциала в контуре строят потенциальную диаграмму , где R – текущее значение сопротивления при обходе контура.

1.2. Содержание задания

Для заданного варианта исходных данных:

1. Составить систему уравнений по законам Кирхгофа в символьном виде.

2. Рассчитать токи в ветвях методом контурных токов.

3. Рассчитать токи в ветвях методом узловых напряжений.

4. Проверить баланс мощности.

5. Используя метод эквивалентного источника напряжения, найти ток в ветви с сопротивлением R₁.

6. Рассчитать потенциалы в точках соединения элементов внешнего контура, включая ветви, соединенные с землей.

Построить потенциальную диаграмму.

1.3. Указания к расчету

1. Выбор варианта.

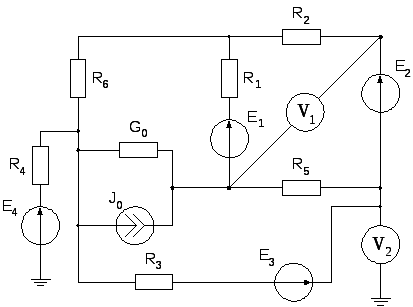
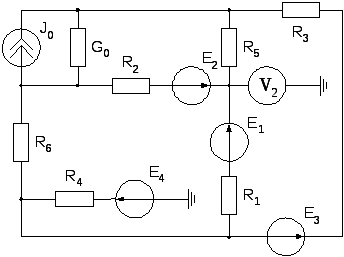
Вариант задания определяется двумя цифрами: 1-я цифра соответствует номеру схемы электрической цепи (1 – 24); 2-я цифра – соответствует номеру строки из таблицы 1 [3].

Таблица 1

№	J	E1	E2	E3	E4	E5	E6	G	R1	R2	R3	R4	R5	R6	R7	R8	R9
	А	В	В	В	В	В	В	1/Ом	Ом	Ом	Ом	Ом	Ом	Ом	Ом	Ом	Ом
1	10	110	110	220	220	100	100	0,2	6	8	15	4	10	15	2	8	5
2	12	110	220	110	110	100	110	0,2	10	15	12	8	12	9	2	5	6
3	10	220	110	110	220	220	110	0,4	15	12	8	16	20	20	4	6	5
4	5	200	150	200	150	100	110	0,1	20	15	25	18	12	20	8	8	6
5	6	100	120	80	100	110	220	0,1	25	18	12	20	20	15	10	12	8
6	10	110	110	120	120	150	200	0,2	16	12	16	20	15	15	4	10	8
7	10	100	100	110	110	120	160	0,1	16	20	25	18	22	30	10	14	10
8	12	120	120	130	100	150	200	0,1	25	15	18	10	12	18	10	20	15
9	8	130	130	140	100	120	120	0,2	15	10	10	12	8	10	14	8	10
10	12	150	150	140	140	110	100	0,4	20	15	10	8	6	8	12	5	6
11	4	100	50	100	50	100	60	0,2	6	9	15	7	20	10	16	7	9
12	8	50	100	70	90	120	80	0,3	9	6	7	16	15	9	20	13	10
13	10	110	80	120	110	140	100	0,4	30	7	20	6	10	15	14	7	14
14	12	90	100	60	120	160	120	0,3	25	9	7	16	6	18	6	10	20
15	14	100	40	120	60	180	140	0,2	9	18	16	10	19	16	40	20	6

2. При выполнении пунктов 1-5 необходимо исключить из схемы электрической цепи ветви, содержащие вольтметры. Следует обратить внимание на то, что такие ветви могут быть образованы из двух полуветвей, соединенных с землей.

Для получения системы уравнений узловых напряжений и контурных токов следует выполнить следующие действия:

– в соответствии с количеством независимых узлов и контуров записать уравнения в общем виде (1) и (3);

– записать в символьном виде и рассчитать коэффициенты левой части и правую часть каждого из уравнений системы; подставить полученные значения коэффициентов и правой части в исходные уравнения;

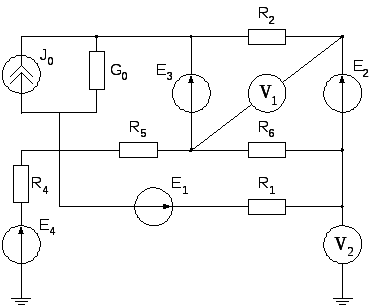
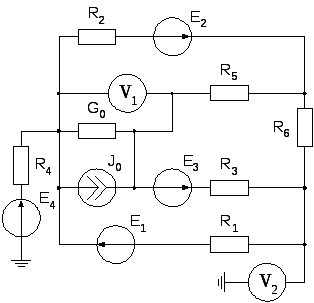
Рис.1	Рис.2
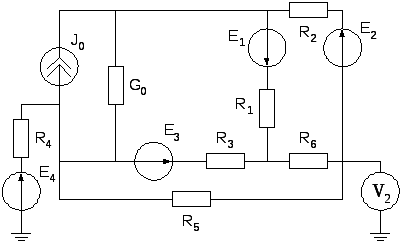
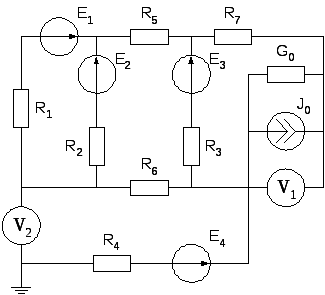
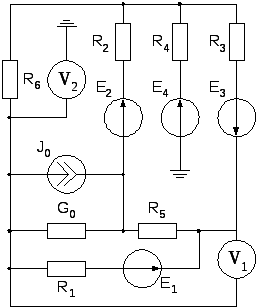
Рис.3	Рис.4
Рис.5	Рис.6
Рис.7	Рис.8
Рис.9	Рис.10
Рис.11	Рис.12
Рис.13	Рис.14
Рис.15	Рис.16
Рис.17	Рис.18
Рис.19	Рис.20
Рис.21	Рис.22
Рис.23	Рис.24

3. Решение уравнений после подстановки численных значений коэффициентов и правой части в каждое из уравнений выполняется на ЭВМ.

4. Показания вольтметров находят для заданной электрической цепи с учетом ветвей, соединённых с корпусом (землёй).

Предварительно указывают положительное направление напряжения вольтметра и выбирают произвольный контур, включающий ветвь с вольтметром. По закону Кирхгофа для напряжений составляют уравнение, решив которое, находят напряжение . В тех случаях, когда вольтметр присоединен к узлам с известными напряжениями, его показания находят как разность узловых напряжений.

5. Проверка баланса мощности производится в соответствии с указаниями и формулами, приведенными в разделе 1.1.4.

6. Расчет э.д.с. и внутреннего сопротивления эквивалентного источника напряжения рекомендуется (по указанию преподавателя) выполнить дважды.

6.1. На основании закона Кирхгофа для напряжений и методов эквивалентного преобразования электрической цепи расчет U₀ = Е_эк и R_вх = R₀ производится в следующем порядке:

- представить схему электрической цепи после исключения из расчетной ветви сопротивления R; полярность напряжения U₀ в разрыве ветви определяется направлением тока I, принятом в начале расчёта;

– составить уравнение для произвольного контура, включающего U₀, по закону Кирхгофа для напряжений;

– рассчитать неизвестные токи, входящие в уравнение контура, используя метод узловых напряжений (в частном случае метод 2-х узлов);

– найденные токи подставить в уравнение для произвольного контура и решить его относительно U₀.

- расчет входного сопротивления относительно выводов разомкнутой ветви производится для пассивной цепи на основании эквивалентного преобразования «треугольник» - «звезда» или «звезда» - «треугольник».

6.2. На основании метода узловых напряжений и метода контурных токов. Порядок определения параметров эквивалентного источника напряжения и пример расчёта их на основании этих методов представлен в приложении .

7. Представить схему контура, для которого предстоит выполнить расчет потенциалов. Ввести обозначение точек соединения элементов и указать направление э.д.с. и тока на каждом расчетном участке. Расчет производится в соответствии с выражениями, приведенными в разделе 1.1.5. По данным расчета, представленным в форме таблицы, строится потенциальная диаграмма.

Таблица 2

R, Ом
U, В

2. АНАЛИЗ УСТАНОВИВШЕГОСЯ СИНУСОИДАЛЬНОГО РежимА В ЧАСТОТНОЙ ОБЛАСТИ

Задачей анализа установившегося синусоидального режима является расчет амплитуды и фазы соответствующей реакции (тока иди напряжения) электрической цепи при воздействии на входе ее источника сигналов синусоидальной формы. В отличие от реакции цепей при постоянной внешнем воздействии, синусоидальные напряжения u(t) токи являются периодическими функциями времени. Связь между ними на элементах L и С описываются известными дифференциальными или интегральными уравнениями. Используя алгебру комплексных чисел, можно интегрально-дифференциальные уравнения относительно действительных функций u(t) и преобразовать в уравнения алгебраические относительно их комплексных амплитуд [1], которые не зависят от времени и являются функциями угловой частоты ω. По окончании расчета, выполненного относительно комплексных величин, необходимо осуществить обратное преобразование комплексных токов и напряжений в действительные функции тока и напряжения u(t). Такой подход к анализу установившегося синусоидального режима находит широкое применение в теории электрических цепей. Он является одним из простейших методов анализа в частотной области и называется комплексным методом или методом комплексных амплитуд.