
- •Математика
- •Утверждено редакционно-издательским советом ВоГту Составитель: Абильдин а.А., канд.Техн.Наук, доцент
- •Введение
- •Тема 1. Векторы. Линейные операции над векторами.
- •§1.1. Действия над векторами.
- •3.Скалярное произведение
- •1.3.Линейная зависимость и независимость векторов
- •Тема 2. Матрицы и определители
- •1.Транспонирование матриц
- •2. Сложение
- •3.Умножение матрицы на скаляр
- •4.Умножение матриц
- •§2.2. Обратная матрица
- •Тема 3. Решение систем линейных уравнений
- •Тема 4. Произведение преобразований
- •Тема 5. Собственные векторы линейных преобразований
- •Тема 6. Комплексные числа
- •Контрольная работа № 1
- •Тема 8. Предел и непрерывность функций
- •Тема 9. Производная и дифференциал
- •Исследование функций
- •Тема 10. Приближенное решение уравнений
- •Контрольная работа №2
- •Литература
Контрольная работа № 1
Задание 1. Решить систему уравнений методом Гаусса и с помощью обратной матрицы
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 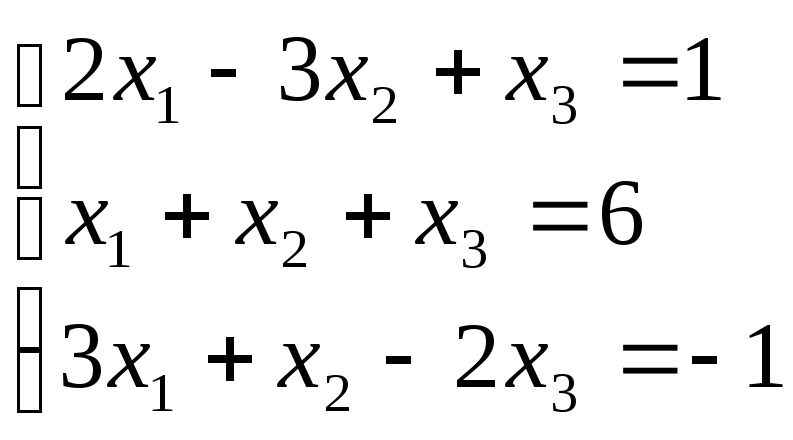
10. 
11. 
12. 
13. 
14. 
15. 
6. 
17. 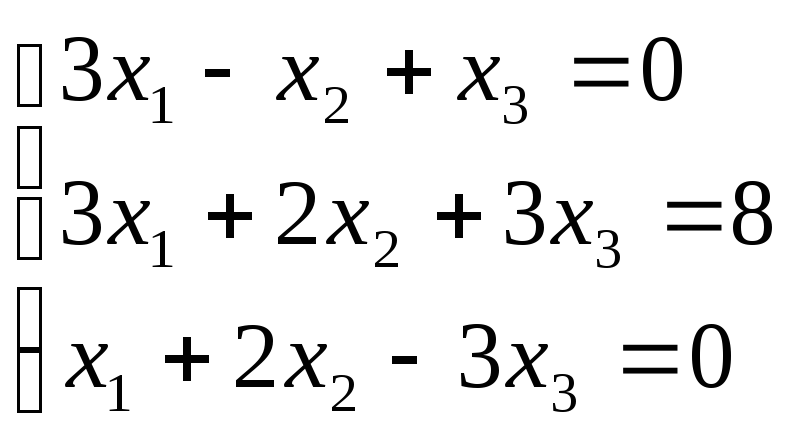
18. 
19. 
20. 
21.
![]()

22. 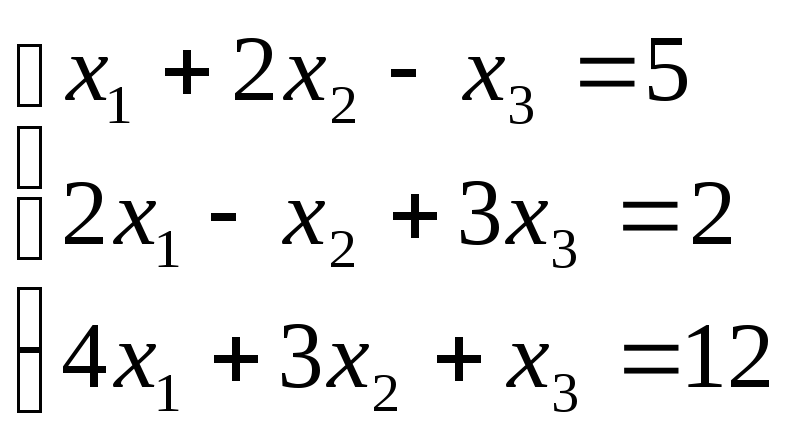
23. 
28.

24.

25. 
26. 
27. 
![]()
![]() 29.
29. ![]()

30.

![]()
Задание 2.
В
задачах 1-30 даны два линейных преобразования.
Средствами матричного исчисления найти
преобразование, выражающее X"= черезX=
черезX=![]()
1.


2.


3.


4.


5.


6.


7.


8.


9.
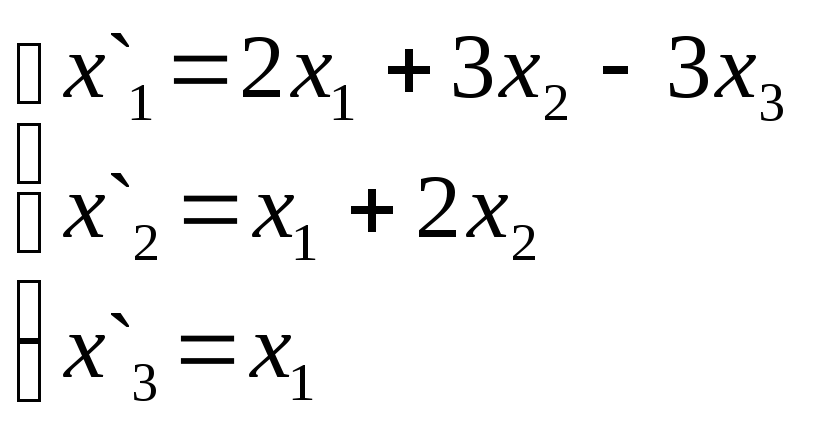

10.
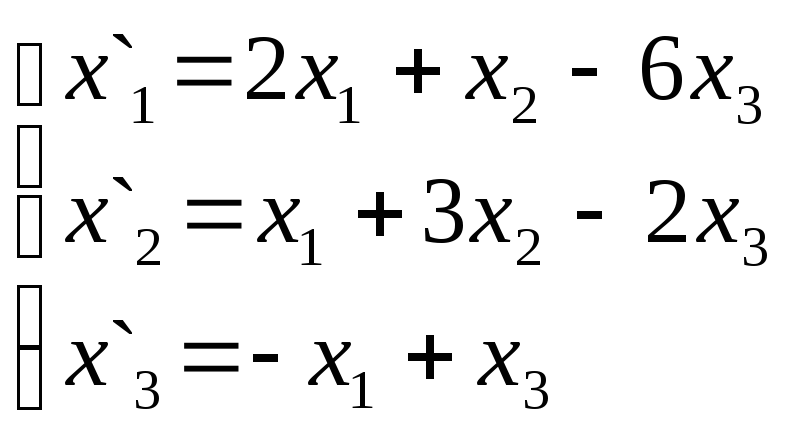

11.


12.


13.

14.


15.

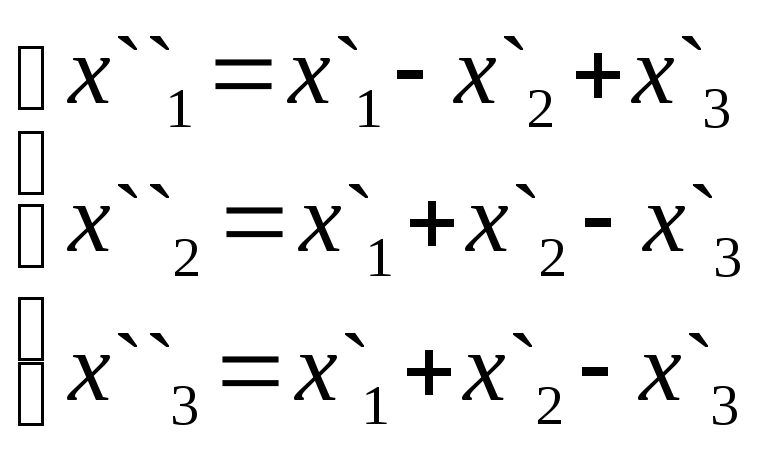
16.


17.


18.

19.

20.

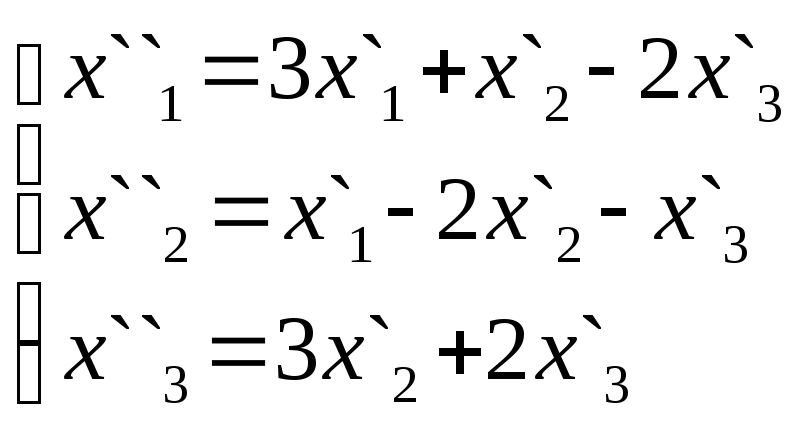
21.


22.


23.


24.

25.

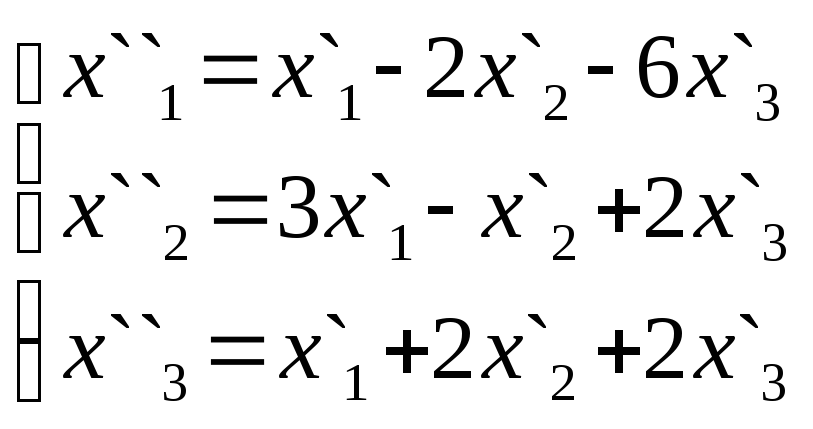
26.


27.
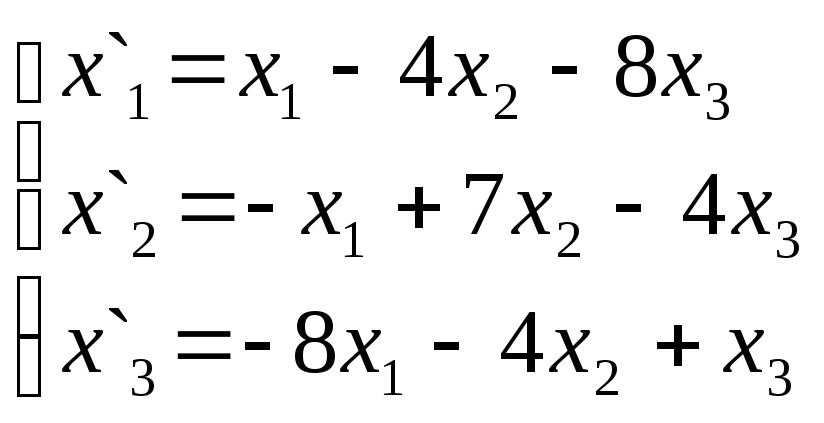

28.


29.


30.


Задание 3.
Найти собственные векторы и собственные значения линейного преобразования, заданного в некотором базисе матрицей.
1.
 2.
2.
 3.
3.

4.
 5.
5.
 6.
6.

7.
 8.
8.
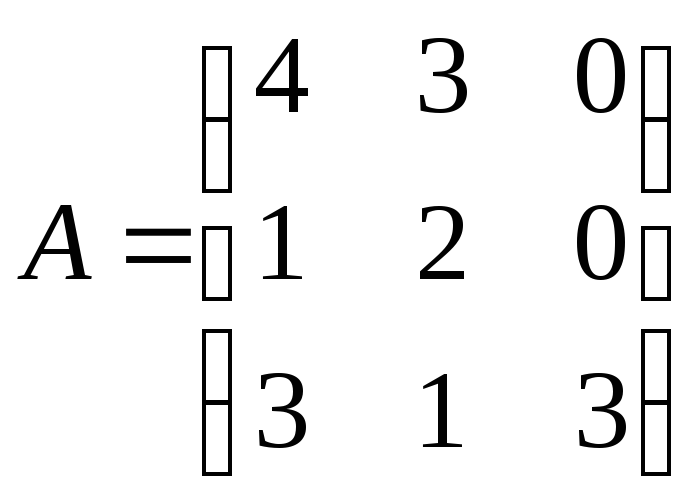 9.
9.

10.
 11.
11.
 12.
12.

13.
 14.
14.
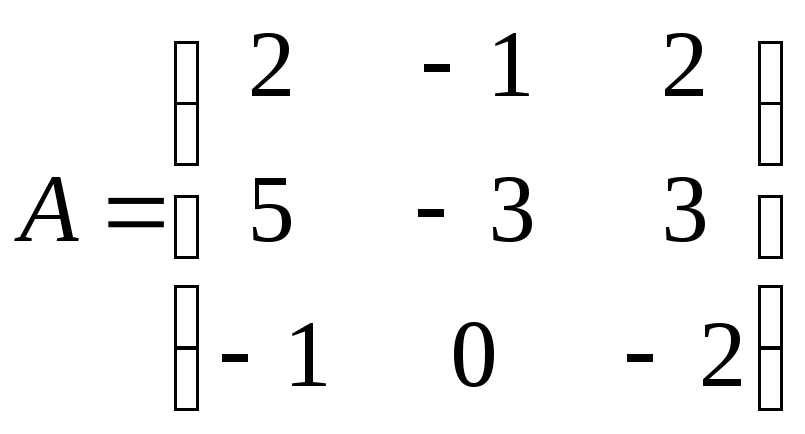 15.
15.

16.
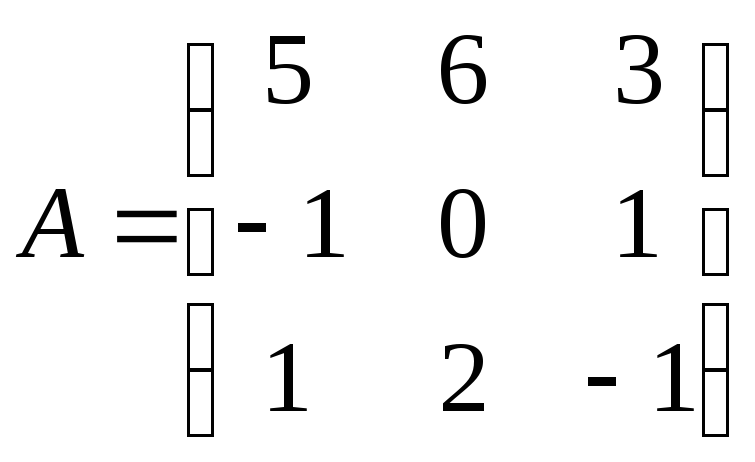 17.
17.![]() A=
A= 18.
18.

19.
 20.
20.
 21.
21.

22.
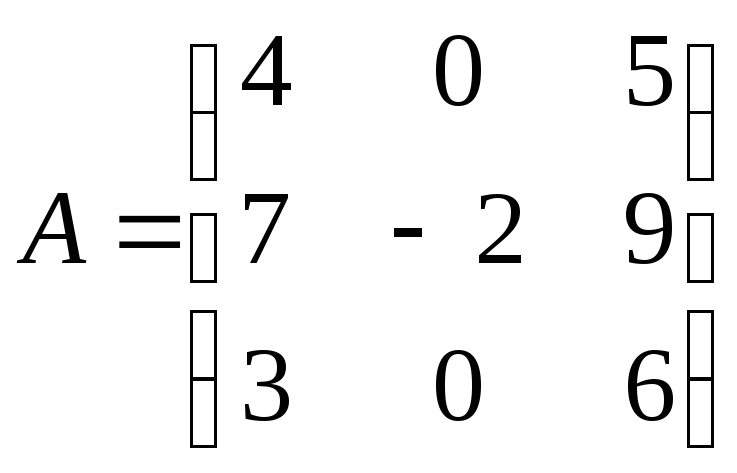 23.
23.
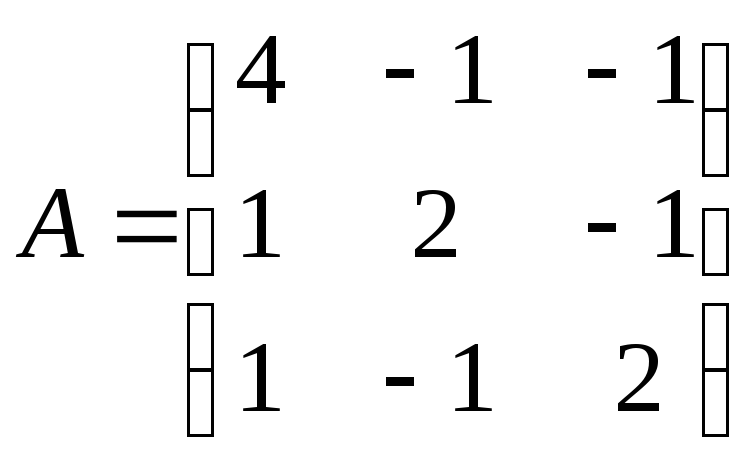 24.
24.

25.
 26.
26.
 27.
27.

28.
 29.
29.
 30.
30.

Задание 4.
Дано
комплексное число
![]() :
:
Записать число
 в алгебраической и тригонометрической
формах.
в алгебраической и тригонометрической
формах.Найти и изобразить на плоскости все корни уравнения Z3 +
 = 0.
= 0.
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]() 7.
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]() 11.
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]() 15.
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]() 19.
19.
![]() 20.
20.
![]()
21.
![]() 22.
22.
![]() 23.
23.
![]() 24.
24.
![]()
25.
![]() 26.
26.
![]() 27.
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]()
Тема 8. Предел и непрерывность функций
Не повторяя данных в учебнике определений и доказательств, рассмотрим ряд конкретных примеров, в которых отражена сущность теории пределов.
Пример 1.

![]()
Подстановка
на место x его предельного значения,
т.е. числа 2, приводит к неопределенности
вида
![]() .
Преобразуем дробь
.
Преобразуем дробь
![]() до перехода к пределу, разложив числитель
и знаменатель на множители
до перехода к пределу, разложив числитель
и знаменатель на множители
![]()
![]()
теперь
имеем
![]() .
.
Пример 2.

Подстановка
предельного значения x
( т.е. числа 0) приводит к неопределенности
вида
![]() .
Преобразуем дробь под знаком предела
до того как
.
Преобразуем дробь под знаком предела
до того как
![]() .
.
![]()

![]()
![]() =
=![]() .
.
Пример 3.
Найти
![]() .
.
Здесь
выражение под знаком пределов представляет
собой отношение двух многочленов
аргумента n.
И числитель и знаменатель дроби стремятся
к бесконечности. В этом случае говорят,
что имеется «неопределенность типа
![]() ».
».
Для отыскания предела следует раскрыть скобки и разделить числитель и знаменатель на высшую степень.
Получаем

Так
как
![]() при
при![]() .
.
Пример 4.
Найти
![]() .
.
Как
и в примере 3 целесообразно числитель
и знаменатель дроби разделить на старшую
степень, которую легко увидеть, если
под каждым корнем оставить лишь старшую
степень n
(остальные слагаемые играют малую роль
при
![]() ).
).
В
данном примере получаем
 .
.
Значит
старшая степень -x.
Разделив числитель и знаменатель на x,
будем иметь ,
так как
,
так как
![]() при x
при x![]()
Пример 5.
Найти
![]() .
.
Здесь
мы имеем «неопределенность типа (![]() )».
)».
Умножив
и разделив эту разность на сопряженное
выражение
![]() ,
получим
,
получим![]()
.
Такой
предел рассматривался в предыдущем
примере. Разделив числитель и знаменатель
на x,
будем иметь
![]() .
.
![]()
Пример 6.
Вычислить
![]()
Здесь
основание степени
 при x
при x![]() ,а
показатель
,а
показатель
![]() ;
таким образом имеем «неопределенность
типа
;
таким образом имеем «неопределенность
типа
![]() ».
В этом случае следует воспользоваться
вторым замечательным пределом:
».
В этом случае следует воспользоваться
вторым замечательным пределом:![]()
![]()
![]() .
.
Преобразовав выражение, получаем
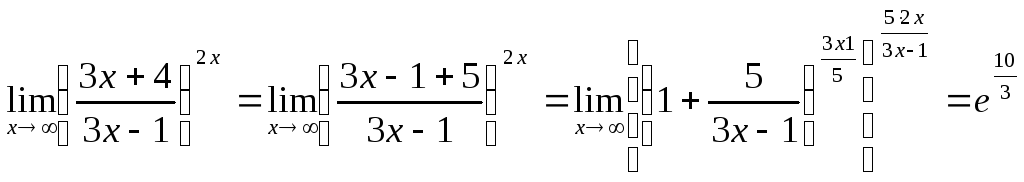 ,
,
так
как выражение в квадратных скобках
стремится к е,
а
![]() при
при![]() .
.
Пусть,
например, требуется вычислить
![]() .
.
Рассмотрим
случай
![]()
![]() ,
тогда показатель стремится к
,
тогда показатель стремится к![]() ,
основание к 4, значит искомый предел
равен
,
основание к 4, значит искомый предел
равен![]() .
Если
.
Если![]() ,
то показатель
,
то показатель![]()
![]() ,основание
стремится к 4 и искомый предел равен 0.
Итак
,основание
стремится к 4 и искомый предел равен 0.
Итак
 .
.![]()
Пример 7.
Найти
![]() .
.
Для
решения применим предел
![]()
Здесь
при
![]() и
числитель и знаменатель стремятся к
нулю, получаем «неопределенность типа
и
числитель и знаменатель стремятся к
нулю, получаем «неопределенность типа
![]() ».
Используя формулу тригонометрии
».
Используя формулу тригонометрии
имеем
![]()
Заметим,
что cos(15x)![]() приx
приx![]() ,
поэтому
,
поэтому
![]()
Пример 8.
Найти
![]() .
.
Известно
( следствие теоремы Безу), что если
многочлен обращается в нуль при
![]() , то он
делится без остатка на
, то он
делится без остатка на
![]() ,
поскольку и числитель и знаменатель
рассматриваемой дроби обращается в
нуль при х=1 «неопределенность типа
,
поскольку и числитель и знаменатель
рассматриваемой дроби обращается в
нуль при х=1 «неопределенность типа
![]() »,
то как и в предыдущей задаче, можно
сократить дробь на х-1. Разделив числитель
и знаменатель на x-1
»,
то как и в предыдущей задаче, можно
сократить дробь на х-1. Разделив числитель
и знаменатель на x-1


получаем
![]() .
.
Пример 9.
Найти
точки разрыва функции
![]() .
Изобразить график в окрестности точки
разрыва.
.
Изобразить график в окрестности точки
разрыва.
Знаменатель
![]() ,
при х=1 обращается в нуль и значит f(x)
при x=1
не существует, следовательно, x=1
- точка разрыва функции. Для определения
типа разрыва надо найти пределы функции
слева и справа при х=1.
,
при х=1 обращается в нуль и значит f(x)
при x=1
не существует, следовательно, x=1
- точка разрыва функции. Для определения
типа разрыва надо найти пределы функции
слева и справа при х=1.

При
тех же рассуждениях получим
![]() .
.
![]()
Итак,
пределы функции слева и справа при
![]() равны, но в точке x=1
функция не определена, значит, точка
устранимого разрыва. График функции в
окрестности точки разрыва выглядит
следующим образом:
равны, но в точке x=1
функция не определена, значит, точка
устранимого разрыва. График функции в
окрестности точки разрыва выглядит
следующим образом:

Такой разрыв называют устранимым разрывом, так как доопределив функцию f(x) надлежащим образом (положив при x=1 f(x) =4) получим непрерывную функцию:
 .
.
