1.3. Теория погрешностей.

Теория погрешностей является приложением выводов теории вероятностей к нахождению правил, с помощью которых мы можем составить общее суждение о точности измерения и точности результата. Это суждение должно быть объективным; именно для этого надо, чтобы оно производилось по определенным правилам и выражалось числами. Цель теории погрешностей и состоит в формировании этих правил. Каждое измерение заключает в себе некоторую степень неточности, зависящую от ошибок наблюдателя (совпадение двух черточек, оценивание на глаз части деления, т.д.) и чувствительности применяемых методов и приборов (весов, термометров, бюреток и т.п.). Учет этих погрешностей в окончательных заключениях является основным вопросом, стоящим перед экспертом, и от разрешения их зависит ценность исследования. Метод (математическая база) теории погрешностей – элементы теории вероятностей (нормальный закон распределения случайных величин, обработка распределенных по гауссову закону результатов измерений) и элементы дифференциального исчисления.

Теория погрешностей изучает только погрешности, которые остаются после исключения систематических погрешностей и просчетов/промахов; они называются случайными. Иначе говоря, случайные погрешности и составляют предмет теории погрешностей, а задачей теории погрешностей является оценивание случайной составляющей погрешности результата измерений. Анализ случайной погрешности допускает математическую формализацию, что дает право говорить о теоретических аспектах науки о погрешностях. Случайные погрешности не следуют какой либо определенной закономерности, выражающей значение погрешности в зависимости от времени или какой-либо иной независимой переменной. Они следуют тем законам, которые выводятся в теории вероятностей по отношению к повторению так называемых случайных явлений.

Так, при повторных, даже самых тщательных, измерениях одной и той же величины получаются более или менее расходящиеся результаты. Так как впоследствии необходимо оперировать одним определенным значением, то вводятся известные условия и способ его вычисления. Самый простой и правомерный способ – это взять из полученных чисел среднее арифметическое. Если x₁, x₂ , ..., x_i, ... x_n представляют собой n экспериментальных данных, то как вероятнейшее значение берут

.

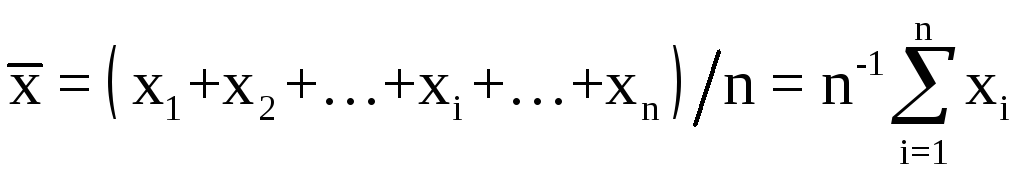Отклонения от среднего арифметического для каждого опыта будут:

_=–x₁, _=–x₂, … _i=–x_i, … _n=–x_n.

На основании определения x мы имеем очевидно: .

Покажем теперь, что сумма квадратов отклонений

есть минимум также вследствие принятого определения числа , счи­таемого наивероятнейшим результатом. Предположим, что– число пока неопределенное, и будем рассматривать сумму квадратов откло­нений, как функцию . Для нахождения условия, при котором сумма квадратов отклонений дает минимум, приравняем первую производную этой функции нулю, в результате чего получим. То есть значение, при котором сумма квадратов отклонений становится ми­нимальной, является средним арифметическим значением величины x. Эта теорема впервые была доказана Гауссом, а такой способ выравни­вания ошибок носит название метода наименьших квадратов (см.Приложение E). Вышеуказанный способ отыскания наивероятнейшего значения правомерен только при большом числе измерений, когда слу­чайные ошибки подчиняются следующей закономерности:

1) существует одинаковая вероятность для равных по модулю положительных и отрицательных погрешностей (т.е. при очень большом числе измерений одной и той же величины равные, но противоположного знака погрешности одинаково часто встречаются);

2) для различных измерений одной и той же величины можно найти такое число k, что все случайные погрешности будут заключаться между +k и –k, причем наименьшие будут встречаться наиболее часто [92].

Изложенные соображения приводят к формулировке постулатов теории погрешностей.