1.3.1. Постулаты.

В основе теории погрешностей лежат три следующих постулата, не доказанных (а может быть и недоказуемых) теоретически, но подтвержденных практикой.

1. Принцип арифметического среднего – арифметическое среднее из ряда результатов измерений физической величины одинакового достоинства есть наиболее вероятное значение измеряемой величины.

2. Правило больших чисел – при большом числе измерений случайные погрешности одинакового значения, но разного знака, встречаются одинаково часто.

3. Закон Гаусса – плотность вероятности распределения результатов измерений описывается выражением

где– среднее арифметическое результатов измерений, – дисперсия результатов измерений. Иначе говоря, большие по абсолютному значению погрешности встречаются реже, чем малые. Вид этой зависимости показан на рис. 1.3.1 для =0 и=1. Здесь использовано общепринятое обозначение гауссовой плотности вероятности распределенияErf(x).

Р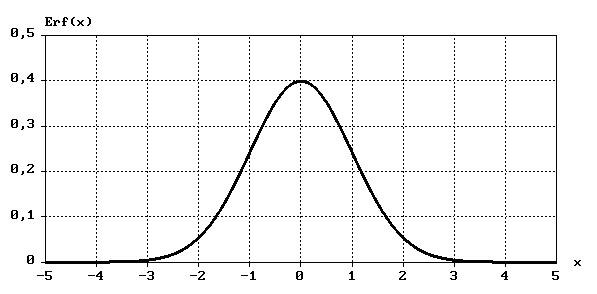ис. 1.3.1. Распределение ошибок по закону Гаусса.

ПРИМЕЧАНИЕ. Область применимости постулатов – случай отсут­ствия динамики систематических погрешностей. Случай на практике отнюдь не всеобъемлющий, хотя бы из-за наличия трендов.

1.3.2. Математические основы теории погрешностей.

Свойства гауссова распределения. Рассмотрим спектральные свойства гауссовой функции [95].

Во-первых, она четная, следовательно, ее фурье-образ действителен (и тоже является четной функцией). Физический смысл этого вывода за­ключается в том, что все компоненты разложения имеют одинаковую фазу "в нулевой момент времени".

Во-вторых докажем следующую теорему: Фурье-образ^ одного гауссова распределения представляет собой другое гауссово распределение. На рис. 1.3.2A (слева) изображена гауссова кривая погрешностей высотой , зеркально симметричная относительно оси ординат x=0

Р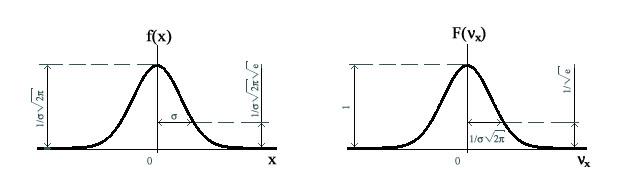ис. 1.3.2A. Слева гауссова кривая погрешностей,

справа – ее фурье-образ.

(т.е. при=0) и описываемая выражением

(1)

где – параметр ширины кривой, именуемый стандартным отклонением; он равен тому значению абсциссы x, при котором ордината в раз меньше максимума. Кривая погрешностей, естественно, и нормируется так, чтобы площадь под ней была равна единице:

.

Фурье-образ гауссовой функции имеет вид:

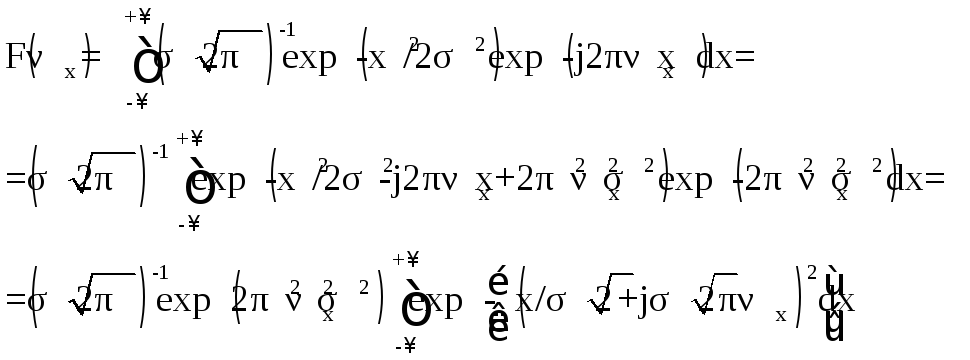
Произведем замену переменной:

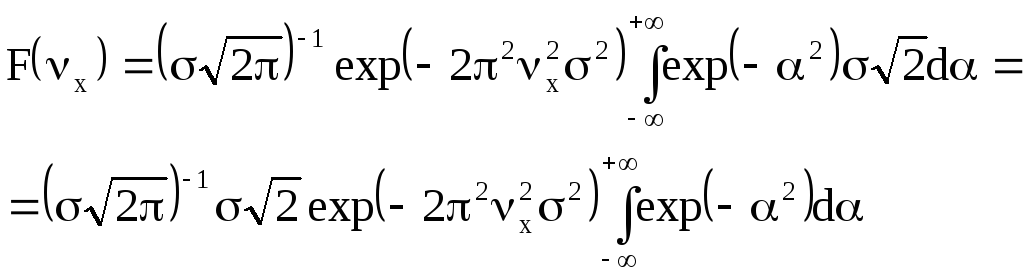
Учитывая, что [96, № 860.11], получим:

(2)

Это тоже гауссово распределение (но в пространстве частот _x – рис. 1.3.2A справа) с другой – единичной – высотой и другим параметром ширины . На обоих графиках (справа и слева) кривые построены в одном масштабе: при они, как и следует из (1) и (2), совпадают. Посмотрим, что произойдет с кривыми при вариации . На рис. 1.3.2B приведены два семейства кривых: самих гауссовых функций

Р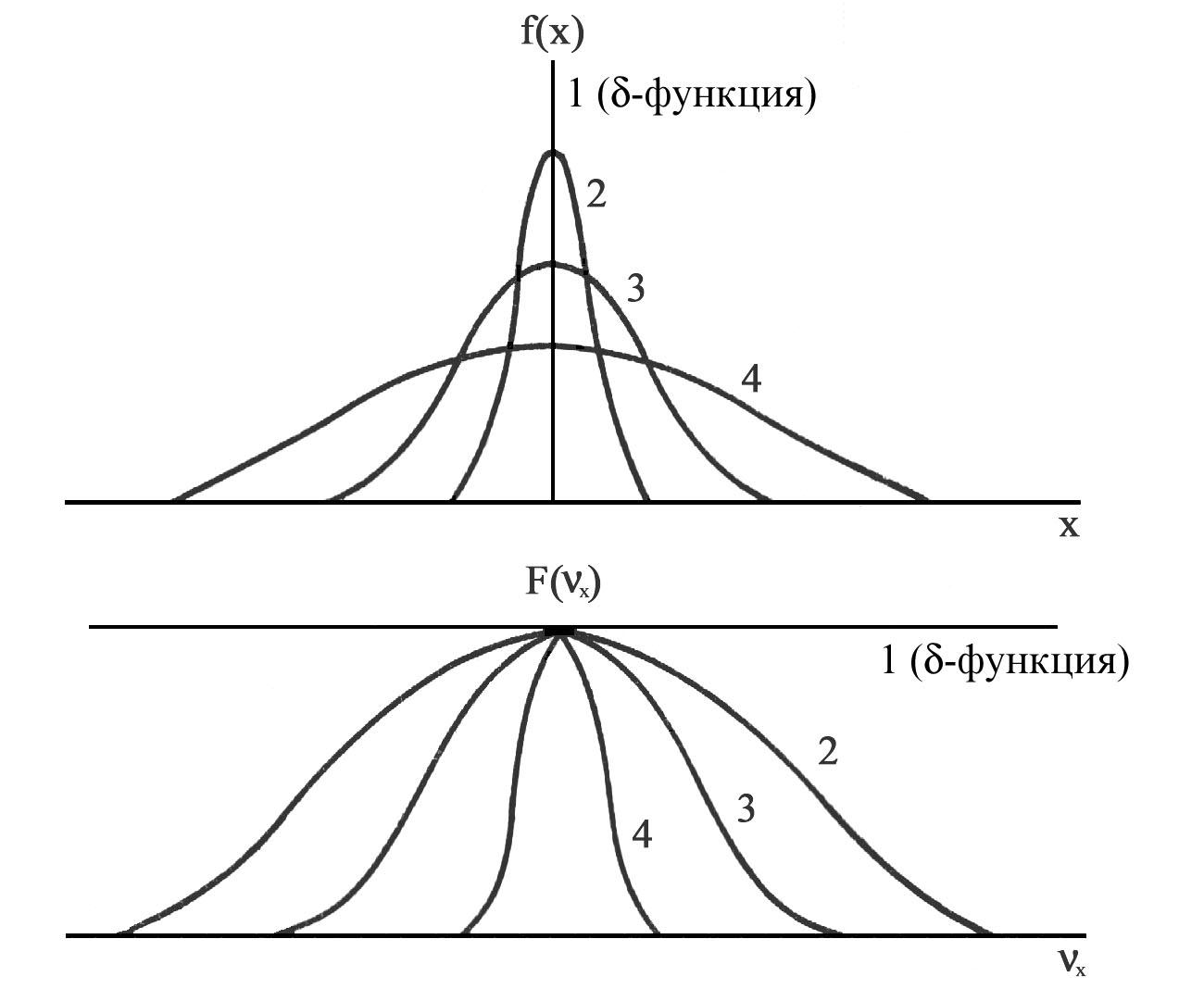ис. 1.3.2B. Зависимость формы кривых от стандартного отклонения.

(сверху) и их фурье-образов (внизу). Графики помечены соответствующими значениями . Любопытно, что предельные зависимости описываются-функцией и единичной константой, соответственно узкое распределение погрешностей преобразуется в широкий фурье-спектр и наоборот. Остается упомянуть, что в теории вероятностей [103] фурье-образ функции распределения называют характеристической функцией.