- •Кафедра прикладной физики На правах рукописи
- •Начала метрологии.
- •1.1.2. Метрологическая терминология.
- •Результат наблюдения неисправленный
- •1.2. Учение об измерениях.
- •1.2.1. Понятия и категории измерений.
- •1.2.2. Сигнал измерительной информации.
- •1.2.3. Искажение измерительной информации.
- •1.2.4. Классификация измерений.
- •1.2.5. Методы измерений.
- •1.2.6. Уравнение измерений.
- •1.2.7. Систематические погрешности.
- •Виды систематических погрешностей
- •1.3. Теория погрешностей.
- •Покажем теперь, что сумма квадратов отклонений
- •1.3.1. Постулаты.
- •1.3.2. Математические основы теории погрешностей.
- •1.3.3. Практическое оценивание погрешностей.
1.3.3. Практическое оценивание погрешностей.
Правила оценивания погрешностей измерений определяются, естественно, по-разному применительно к измерениям однократным и многократным. В обоих случаях они существенно отличаются для измерений прямых и косвенных (совместные и совокупные измерения мы вообще оставим в стороне).
Но даже при привычных нам многократных измерениях правила проведения оценивания погрешностей отнюдь не всеобъемлющи и наиболее строго регламентированы лишь для нормально распределенных данных. В случае априорно неизвестного распределения алгоритм оценивания предусматривает обязательную проверку данных на соответствие гауссову закону. Порядок ее проведения изложен в Приложении D.
По-отдельности процедуры оценивания погрешностей рассмотрены в Приложениях A, B и C. Оговоримся сразу, что для каждого из рассматриваемых случаев там использована своя собственная нумерация разделов и формул. Для экспертов же особый интерес представляет проблема исключения промахов.
Исключение промахов. Критерий Шовене.
В этой лекции мы остановимся на довольно щекотливом вопросе, учитывать ли результат измерений, который до такой степени кажется несуразным, что скорее похож на промах.
Сначала обсудим саму проблему отбрасывания данных. Подчас результат одного измерения из серии поразительно отличается от всех остальных. В этом случае эксперт должен решить, является ли такой аномальный результат измерения следствием промаха и, как следствие, его надлежит отбросить, или же это вполне правомерный результат, который должен обрабатываться далее наряду с другими. Например, представим себе, что мы проводим шесть измерений фокусного расстояния объектива, получая следующие результаты (в миллиметрах)
38; 35; 39; 39; 34; 18. (1)
В этом примере значение 18 заметно разнится с прочими, и нам надо решить, что же с ним делать дальше.
Очевидно, единичный результат нормального распределения может существенно различаться с результатами других измерений того же фокусного расстояния. Тем не менее, в штатной ситуации столь значительное отличие, как это наблюдается в (1), очень маловероятно; посему мы имеем полное право предположить, что расстояние 18 мм является следствием некой незамеченной ошибки или обусловлено неким сторонним фактором. Возможно, считывая последнее показание со шкалы, мы просто ошиблись и записали неверное число; возможно, перед последним замером была сдвинута линейка, отчего сбилась установка начала отсчета; возможны и иные причины.
Если бы мы дотошно контролировали каждое измерение, то иногда смогли бы объяснить возможную причину появления аномального результата. К примеру, тщательная запись в лабораторном журнале показала бы, что перед последним измерением подстраивалось напряжение на используемом источнике излучения, а последующая проверка могла бы выявить отличие по спектральному составу. Тогда, естественно, аномальный результат подлежит исключению однозначно.
К сожалению, аномальности отдельного результата обычно не удается поставить в соответствие определенную стороннюю причину. В этом случае надо решать, исключить такой результат или нет, отталкиваясь лишь от самих полученных значений, – и здесь наиболее плодотворным оказывается подход, основанный на свойствах гауссова распределения.
Вообще, надо сказать, что отбрасывание данных – спорный вопрос, по которому у теоретиков единого мнения до сих пор не сложилось. Но это еще и исключительно важный вопрос для практиков. В приведенном выше примере качество оценки фокусного расстояния в достаточной мере зависит от того, отбросим ли мы сомнительное значение 18 мм. Среднее арифметическое по шести измерениям составляет 34 мм, в то время как по пяти измерениям – 37 мм, т.е. почти на десять процентов больше.
Помимо того, решение исключить из рассмотрения какие-либо данные в конечном счете всегда субъективно, и эксперта, который принял это решение, его коллеги могут осудить за подобную "подгонку результатов". Но ситуация осложняется сверх того, если учесть возможное отражение в аномальном результате неких не принятых во внимание эффектов (в самом деле, многие научные открытия выглядели поначалу как аномальные результаты измерений, которые походили скорее на промахи). Исключая значение 18 мм из совокупности результатов (1), мы, возможно, выбрасываем наиболее интересную часть данных.
Единственно честная реакция при встрече с выборкой, подобной (1), – повторить измерения множество раз. Если аномалия проявится снова, нам станет легче выяснять ее причину, будь то промах или неожиданный физический эффект. Если она не повторится, то к тому времени, когда мы в этом убедимся, будет проведено настолько много измерений, что после усреднения не будет особой разницы, учитываем ли мы аномалию при расчете или нет.
Однако, в подавляющем большинстве случаев только на том основании, что один из результатов нам кажется подозрительным, проводить измерения, скажем, 100 раз непрактично, а для объектов экспертизы, подчас, и невозможно. Поэтому необходим критерий, сопоставляя с которым подозрительный результат, мы можем включить его в выборку или отвергнуть. Таких критериев известно несколько, отдельные очень сложны. Мы остановимся одном из самых простых – критерии Шовене, базирующемся, разумеется, на гауссовом распределении.
Теперь займемся собственно критерием Шовене. Вернемся к рассмотренному выше примеру. Полагая, что все значения (1) суть законные результаты измерения фокусного расстояния xi вычислим среднее арифметическое и среднее квадратическое отклонение (с.к.о.)
![]() =34
мм,
(2)
=34
мм,
(2)
![]() =8
мм.
(3)
=8
мм.
(3)
Теперь
можно количественно определить уровень,
показывающий, до какой степени
подозрительный результат аномален.
Значение x6=18
мм отличается среднего арифметического
(2) на 16 мм, или на два с.к.о. Если мы уверены,
что статистика результатов (1) описывается
гауссовым распределением с центром и
шириной, определяемыми выражениями (2)
и (3), то становится возможным вычисление
вероятности получить результат, который,
по крайней мере, так же сильно отличается
от среднего арифметического
![]() .
Вероятность такого результата вычисляется
интегрированием гауссовой плотности
распределения (п. 1.3.1), в метрологии
обычно именуемой функцией ошибок и
обозначаемой
.
Вероятность такого результата вычисляется
интегрированием гауссовой плотности
распределения (п. 1.3.1), в метрологии
обычно именуемой функцией ошибок и
обозначаемой
Н![]() овая
функция, именуется интегралом ошибок
и обозначается:
овая
функция, именуется интегралом ошибок
и обозначается:
![]()
Интеграл
ошибок определяет вероятность того,
что результат будет лежать в интервале
[x=a, x=b]:![]() .
Обычно a и b выражают через среднее
арифметическое, среднее квадратическое
отклонение и число t последних. Поэтому
.
Обычно a и b выражают через среднее
арифметическое, среднее квадратическое
отклонение и число t последних. Поэтому
![]() ,
,
то
есть интеграл ошибок показывает
вероятность того, что результат измерений
окажется в пределах t стандартных
отклонений в любую сторону от
![]() .
Аналитически erf(t) не берется, и мы
воспользуемся его численными оценками
(возможность калькуляции этого интеграла
заложена во многие программные пакеты,
в том числе и наиболее популярныеMATCAD
и MATLAB):
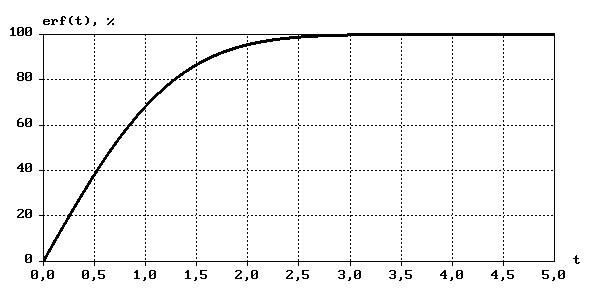
на рис. 1.3.3 эта функция представлена
.
Аналитически erf(t) не берется, и мы
воспользуемся его численными оценками
(возможность калькуляции этого интеграла
заложена во многие программные пакеты,
в том числе и наиболее популярныеMATCAD
и MATLAB):
на рис. 1.3.3 эта функция представлена
|
|
|
Рис. 1.3.3. Интеграл ошибок (основной). |
графически. В соответствии с графиком искомая вероятность равна:
P(вне![]() мм)=1–P(в
интервале
мм)=1–P(в
интервале![]() )=
)=
=1–0,95=
=0,05=5%.
Иначе
говоря, если продолжить измерения,
накапливая результаты сверх 6 в выборке
(1) можно ждать, что только один результат
из 20 будет различаться со средним
арифметическим по крайней мере так же
сильно, как отличается от
![]() подозрительное значение 18 мм. Проведя
20, 40, ... измерений, мы действительно
должны были бы ожидать появления 1, 2,
... результатов хуже 18 мм, и у нас не было
бы никаких оснований исключать их. Но
на самом деле мы успели провести только
6 измерений, соответственно ожидаемое
количество результатов, не менее плохих,
чем 18 мм, равно
подозрительное значение 18 мм. Проведя
20, 40, ... измерений, мы действительно
должны были бы ожидать появления 1, 2,
... результатов хуже 18 мм, и у нас не было
бы никаких оснований исключать их. Но
на самом деле мы успели провести только
6 измерений, соответственно ожидаемое
количество результатов, не менее плохих,
чем 18 мм, равно
0,05∙6=0,3=30%,
другими словами, для исходно имеющихся в распоряжении шести результатов (1) вероятность появления результата, худшего 18 мм, составляет 1/3.
Именно 1/3 есть искомая количественная оценка "нормальности" подозрительного результата. Полагая, что такая вероятность "ну, очень маленькая" мы должны будем заключить, что результат 18 мм – аномальный; что он должен быть исключен, и наоборот. Выбор же предела, за которым результат можно считать маловероятным, – прерогатива эксперта. Критерий Шовене в своей обычной трактовке утверждает, что подозрительный результат надо исключать, когда число измерений, худших, нежели подозрительный результат, ожидается с вероятностью меньше 50%. Понятно, что выбор именно 50% порога принятия решения достаточно произволен: его можно лишь оправдать (соотношение 1:1 представляется достаточно разумным), но не доказать.
Невозможно, пока не найдется внешнее подтверждение ошибочности подозреваемых данных, доказать и правомерность исключения каких-либо данных, как таковую, – корректности ради иногда говорят, что критерий Шовене применяется лишь для обнаружения данных, которые могли бы потом рассматриваться на предмет исключения.
Что
же касается замеров фокусного расстояния
(1), то по критерию Шовене результат 18 мм
надлежит исключить из выборки: 1/3<50%.
Вычислить новые значения
![]() и
и![]() и сравнить их с (2) и (3), чтобы выяснить,
насколько в действительности подозреваемое
значение влияет на результат измерений,
предлагается самостоятельно.
и сравнить их с (2) и (3), чтобы выяснить,
насколько в действительности подозреваемое
значение влияет на результат измерений,
предлагается самостоятельно.
Применим
критерий Шовене к задаче, формулируемой
в самом общем виде. Пусть проводятся
измерения одной и той же физической
величины x: x1
, x2
, ... xi
, ... xn.
По результатам n измерений вычислим
среднее арифметическое
![]() и среднее квадратическое отклонение.
Если некоторый результат (обозначим
его
и среднее квадратическое отклонение.
Если некоторый результат (обозначим
его
![]() )
различается с
)
различается с![]() столь сильно, что вызывает подозрение,
найдем число с.к.о., на которое
столь сильно, что вызывает подозрение,
найдем число с.к.о., на которое![]() отличается от
отличается от![]()
![]() (4)
(4)
Потом
отыщем из графика (рис. 1.3.3) P(вне
![]() )
– вероятность
того, что результат нормального измерения
будет отличаться от
)
– вероятность
того, что результат нормального измерения
будет отличаться от
![]() на t' и более с.к.о. Теперь, умножив ее на
число измерений n, получим ожидаемое
число измерений с результатами, худшими
на t' и более с.к.о. Теперь, умножив ее на
число измерений n, получим ожидаемое
число измерений с результатами, худшими
![]() ,
,
n’=P(вне t’)n.
При
n'<50% подозрительный результат
![]() критерию Шовене не удовлетворяет. Как
следствие, он подлежит исключению из
выборки.
критерию Шовене не удовлетворяет. Как
следствие, он подлежит исключению из
выборки.
Исключив
результат, негодный по критерию Шовене,
нужно, очевидно, вычислить новые
![]() и по
оставшимся данным. Новое значение с.к.о.
станет, естественно, меньше первоначального,
и может так оказаться, что с ним еще
какой-либо из оставшихся результатов
перестанет отвечать критерию Шовене,
...
. Но в
большинстве случаев ситуация исчерпывается
однократным использованием критерия
Шовене.
и по
оставшимся данным. Новое значение с.к.о.
станет, естественно, меньше первоначального,
и может так оказаться, что с ним еще
какой-либо из оставшихся результатов
перестанет отвечать критерию Шовене,
...
. Но в
большинстве случаев ситуация исчерпывается
однократным использованием критерия
Шовене.
Разберем пример из экспертной практики. Известно, что в большинстве случаев для идентификации осколков взрывного устройства при взрывотехнической экспертизе достаточен химический состав материала. Оптимально же для анализа элементного состава металла спектроскопическое исследование. При эмиссионном спектральном анализе по результатам микрофотометрирования 10 спектрограмм одна из исследуемых линий дала следующие значения интенсивности (в относительных единицах)
43; 45; 44; 58; 47; 45; 38; 44; 48; 46, (5)
причем аномалия значения 58 очевидна, а видимых причин к ее объяснению после самой тщательной ревизии не обнаружено. Используем для анализа данных критерий Шовене.
У![]() чтем
все десять отсчетов (5):
чтем
все десять отсчетов (5):![]() =45,8
и=5,1.
Подозрительный отсчет
=45,8
и=5,1.
Подозрительный отсчет
![]() =58
отличается от среднего арифметического
на 12,2 или на
=58
отличается от среднего арифметического
на 12,2 или на
Из
графика на рис. 1.3.3 найдем, что вероятность
появления столь существенного (на
12,2=2,4)
отклонения отдельного результата от
![]() равна
равна
P(вне 2,4=12,2)=1–P(в интервале 2,4)=
=1–0,984=
=0,016=1,6%. (6)
Тысяче
измерений соответствует, таким образом,
16 случаев получения столь большого
разброса, а десяти, следовательно, –
0,16=16% случая. Поскольку 16%<50%, устанавливаемых
критерием Шовене, эксперту следует
исключить результат
![]() (или, по меньшей мере, рассмотреть такую
возможность: причиной появления столь
плохого результата может быть локальный
всплеск чувствительности фотопластинки
или, попросту, обыкновенная грязь на ее
поверхности).
(или, по меньшей мере, рассмотреть такую
возможность: причиной появления столь
плохого результата может быть локальный
всплеск чувствительности фотопластинки
или, попросту, обыкновенная грязь на ее
поверхности).
Второй
отсчет в (5), который может вызывать
подозрение
![]() =38.
При
=38.
При![]() =45,8
и=5,1
(учтены все те же n=10 результатов измерения)
=45,8
и=5,1
(учтены все те же n=10 результатов измерения)
![]() на 1,5
отличается от среднего арифметического
и аналогичные (6) выкладки показывают,
что при этой статистике эксперту стоит
ждать 1,3 случая столь же плохих результатов,
как и
на 1,5
отличается от среднего арифметического
и аналогичные (6) выкладки показывают,
что при этой статистике эксперту стоит
ждать 1,3 случая столь же плохих результатов,
как и
![]() :
:
nP(вне 1,5 =7,8)=100,13=1013%=1,3=130%.
Разумеется, 130%>50% – это означает, что результат для целей экспертизы вполне приемлем.
Исключив
из выборки (5) результат
![]() =58,
а
=58,
а![]() =38
сохраняя, пересчитаем (уже для n=9) новые
среднее арифметическое и с.к.о.:
=38
сохраняя, пересчитаем (уже для n=9) новые
среднее арифметическое и с.к.о.:
![]() =44,4,
=44,4,
=2,9.
Как и следовало ожидать, первое изменилось незначительно (на 3%), второе заметно (на 40%) уменьшилось.
Если
![]() ,
то
,
то![]() – фурье-образ
(в смысле результат фурье-преобразования)
или фурье-спектр функции f(t).
– фурье-образ
(в смысле результат фурье-преобразования)
или фурье-спектр функции f(t).