1.2. Учение об измерениях.

В измерениях практика первична, а обобщение и формализация закономерностей вторичны. Поскольку единой универсальной концепции науки об измерениях нет, да она и не может быть построена, говорят не о теории измерений, а "учение об измерениях".

Предмет учения об измерениях – систематическая погрешность. Задача учения об измерениях – минимизация случайной составляющей погрешности результата измерений. Метод учения об измерениях – перевод случайной погрешности, или ее доли, в систематическую погрешность.

1.2.1. Понятия и категории измерений.

Измерение и оценивание: измерение есть процедура установления соответствия величины значению меры, оценивание – соответствия интервалу значений (интервал может быть и полубесконечным). Зададимся вопросом, почему к погрешности всегда применяют термин оценивание, а не измерение? Потому что погрешности, как это следует из ее определения, не может быть поставлено в соответствие конкретное значение, а может быть приписан лишь интервал, в пределах которого погрешность находится. Термин оценивание используется и в квалиметрии, но термин измерение – исключительно в метрологии. Результат измерения связан с метрологической оценкой предельным переходом (здесь под термином оценка понимается результат операции оценивания).

1.2.2. Сигнал измерительной информации.

В подавляющем большинстве случаев этот сигнал возможно представить одномерной функцией (как правило, временным сигна­лом), намного реже для его описания требуется использование функций двумерных (плоских изображений). Особенности математического опи­сания сигналов и изображений. Существуют, однако, трех- (пространст­венные) и более многомерные формы определения сигналов и преобра­зований.

Из всех вариантов в лекциях мы подробно рассмотрим только двумерные сигналы измерительной информации. Возможные представ­ления сигнала (детерминированный случай): временное – развертка (см. рис. 1.2.2 левый), частотное – спектр (см. рис. 1.2.2 средний), фазовое – фазовый портрет (см. рис. 1.2.2 правый) [109]. Аналитическая связь временного, частотного и фазового представлений сигнала дается парой интегральных преобразований – преобразованием Фурье (временное-частотное) и преобразованием Гильберта (временное-фазовое).

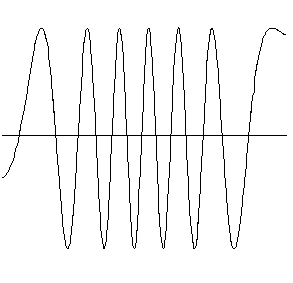
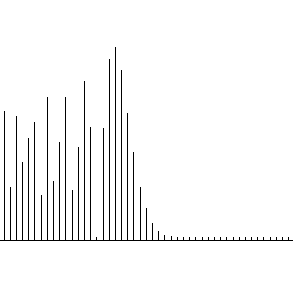
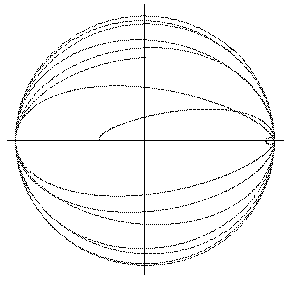
Рис. 1.2.2. Три представления сигнала измерительной информации.

Теорема Винера-Хинчина уже предполагает переход к вероятностному описанию сигнала измерительной информации. Вероятностный же подход наиболее четко отражает и физическую, и метрологическую реальность, включая в себя детерминированный сигнал в качестве частного случая [1], который можно получить предельным переходом, искусственно устремив искажения к нулю.

Временное представление. Рассмотрим измерение некоторой величины x(t), флуктуирующей со временем. На практике иногда удается отыскать распределение вероятностей p(x) ее значений, хотя более типична одновременная доступность измерению ее среднего значения и дисперсии.

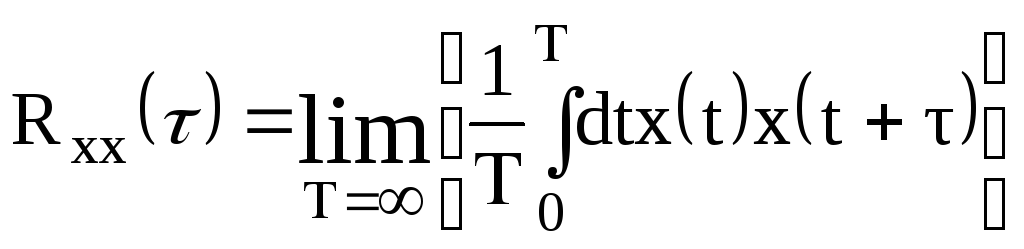Однако среднее и дисперсия очень мало говорят о внутреннем механизме происходящего [80]. В этом плане больший интерес представляла бы величина, служащая мерой влияния значения x в момент t на значение x в момент t+. Такой величиной является автокорреляционная функция, которая, по-видимому, была введена в рассмотрение Тэйлором [81] как

Ее физический смысл – среднее по некоторому временному интервалу T (который потом устремляется к бесконечности) произведения двух значений x, взятых в моменты времени, различающиеся на .

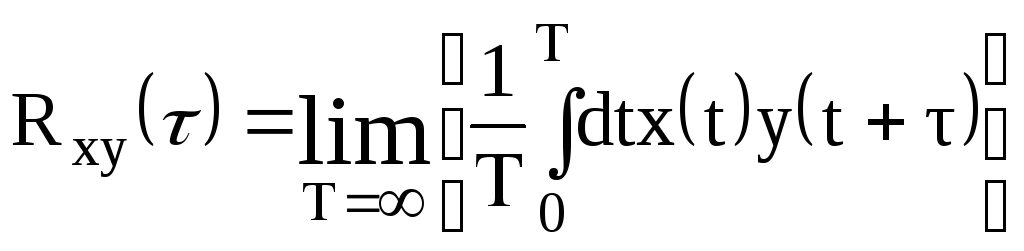Если случайные величины представлены выборочными значениями x(t) и y(t+) разных случайных процессов, то выражение

называется взаимной корреляционной функцией.

Остановимся теперь на аналоговом и цифровом представлениях измерительной информации; в итоге операций дискретизации аргумента и квантования функции мы придем к понятию цифрового сигнала.

Для того, чтобы иметь возможность перенести какую-либо измерительную информацию, сигнал должен быть тем или иным образом преобразован (промодулирован), – в отсутствие модуляции сигнал информации не содержит. Сущность модуляции заключается в изменении какого-либо параметра модулируемого сигнала согласно изменению значений модулирующего (преобразующего) сигнала. Число возможных видов модуляции сигнала равно числу его параметров, которые можно изменять (модулировать). Мы изучим только наиболее часто встречающиеся виды модуляции гармонического (рис. 1) и и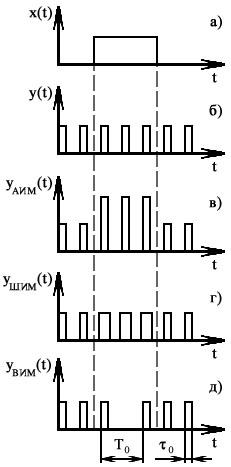мпульсного сигналов (рис. 2).

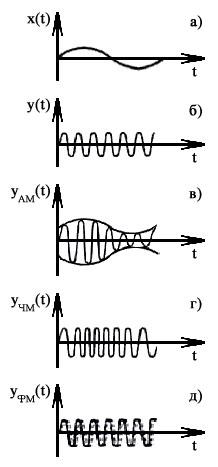
Рис. 1. Виды гармонической модуляции: Рис. 2. Виды импульсной модуляции:

а – модулирующий сигнал; а – модулирующий сигнал;

б – модулируемый сигнал; б – модулируемый сигнал;

в – амплитудная модуляция; в – амплитудно-импульсная модуляция;

г – частотная модуляция; г – широтно-импульсная модуляция;

д – фазовая модуляция. д – время-импульсная модуляция.

Если в качестве модулируемого сигнала берется элементарная сину­соида

,

определяемая амплитудой y₀, частотой ω₀ и фазой φ₀, то в результате воздей­ствия модулирующего сигнала x(t) на y₀ можно получить амплитудную мо­дуляцию (рис. 1в), на ω₀ – частотную модуляцию (рис. 1г) и на φ₀ – фазовую модуляцию (рис. 1д). Аналитически модуляция определяется умножением модулируемого параметра сигнала на множитель 1+m·x(t).

При амплитудной модуляции амплитуда модулированного сигнала из­меняется согласно выражению y(t) = y₀ + ∆y·x(t). Тогда

Глубина модуляции m=∆y/y₀, где ∆y – девиация амплитуды.

При частотной модуляции частота модулированного сигнала изменятся согласно выражению ω(t) = ω₀ + ∆ω·x(t). Тогда

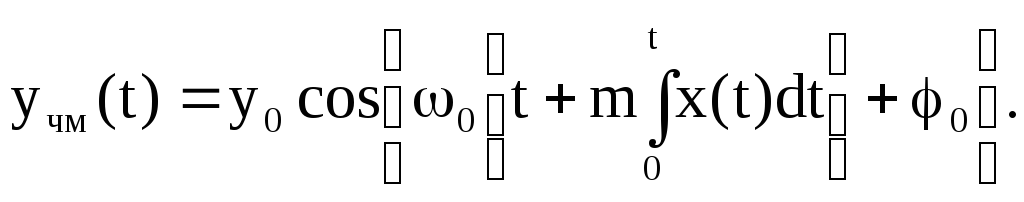
Глубина модуляции m=∆ω/ω_0, где ∆ω – девиация частоты.

При фазовой модуляции фаза модулированного сигнала изменяется со­гласно выражению φ(t) = φ₀ + ∆φ·x(t). Тогда

Глубина модуляции m=∆φ/φ₀, где ∆φ – девиация фазы.

Анализ амплитудной, частотной и фазовой модуляции показал, что мощность модулированных сигналов увеличивается, чем объясняется уве­личение их устойчивости ко всякого рода неинформативным искажениям. Так, при амплитудной модуляции мощность модулированного сигнала в те­чение периода изменяется и ее максимальное значение в 1+m² раз превышает мощность немодулированного сигнала.

Мощность сигнала зависит от вида модуляции. Так, при малом случай­ном искажении флуктуационного типа, т.е. при Р_С Р_И,

где Р_С – мощность сигнала; Р_И – мощность искажения; ß – параметр, в боль­шинстве случаев ß > 1. Из формулы следует, что отношение мощности сиг­нала к мощности искажения при частотной модуляции в 3,3^раза превы­шает это отношение при модуляции амплитудной. Следовательно, частотно-модулированный сигнал более устойчив к искажениям, чем амплитудно-мо­дулированный. Но амплитудная модуляция получила большее распростране­ние в измерительной технике из-за более простой технической реализации.

Модуляция гармонического сигнала используется в основном при пе­редаче по информационному каналу одного сигнала измерительной инфор­мации x(t). Если по одному каналу надо последовательно передавать ряд сигналов, используя коммутацию, то применяются импульсные виды модуля­ции. Импульсный сигнал (рис. 2б) определяется следующим выражением:

t – текущее время; t_i0 – фиксированный момент начала импульсов, T₀ – период импульсного сигнала; τ₀ – длительность импульса.

Так же как и в предыдущем случае, в результате воздействия модули­рующего сигнала x(t) на модулируемый y(t) при воздействии на y₀ можно получить амплитудно-импульсную модуляцию (АИМ), на τ₀ – широтно-им­пульсную модуляцию (ШИМ), на T₀ и t_i0 – время-импульсную модуляцию (ВИМ). Как и для модуляции гармонического сигнала, процесс импульсной модуляции определяется умножением модулируемого параметра на множи­тель 1+mx(t) – см. рис. 2а. Тогда справедливы выражения:

для АИМ

для ШИМ

для ВИМ

Исследование помехоустойчивости импульсной модуляции показало значительное преимущество время-импульсной модуляции. Но наглядность представления модулируемого сигнала, большее быстродействие преобразо­вания сигнала и простота реализации обеспечили много более широкое ис­пользование амплитудно-импульсной модуляции при формировании сигна­лов измерительной информации.

Но, если с помощью модуляции сигнал обогащается измерительной информацией, что происходит, например, в первичных измерительных пре­образователях (в частном случае – датчиках), то дискретизация, квантование и кодирование – уже прерогатива вторичных измерительных преобразовате­лей (в частности – масштабных) и вторичных измерительных приборов. При этом дискретизация и квантование играют одну из основных ролей в инфор­мативной обработке сигнала, кодирование – вспомогательную.

Рассмотрение процессов квантования, дискретизации и кодирования сигналов измерительной информации необходимо не только для изучения свойств сигналов, как таковых, но и для изучения их преобразований, проис­ходящих в цифровых измерительных приборах, для которых эти операции при измерении физических величин являются основными. Так, квантование непрерывного сигнала х(t) производится при любой измерительной опера­ции, когда значение измеряемого сигнала соотносится с какой-либо заданной мерой. Дискретизация и кодирование непрерывного сигнала необходимы для организации передачи множества сигналов по одному каналу, для ввода дан­ных в компьютер с целью их последующей программной обработки, для уменьшения динамической погрешности при регистрации быстропротекаю­щих процессов.

Н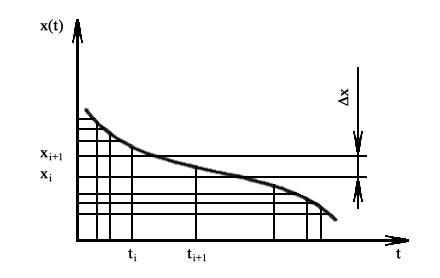аиболее распространенный вид квантования измеряемого сигнала х(t) – это квантование по уровню. При этом преобразовании диапазон изменения непрерывного сигнала представляется значениями, разделенными друг от друга на интервалы квантования ∆х= х_i+1–х_i, где х_i+1 и х_i – это i+1 и i-й уровни квантования. Если ∆х имеют одинаковое значение, то квантование равномер­ное, если они не равны, то квантование неравномерное (рис. 3).

Рис. 3. Неравномерное квантование по уровню.

Сигнал, квантованный по уровню, в функции времени может быть представлен как произведение единичной ступенчатой функции (функции Хевисайда)

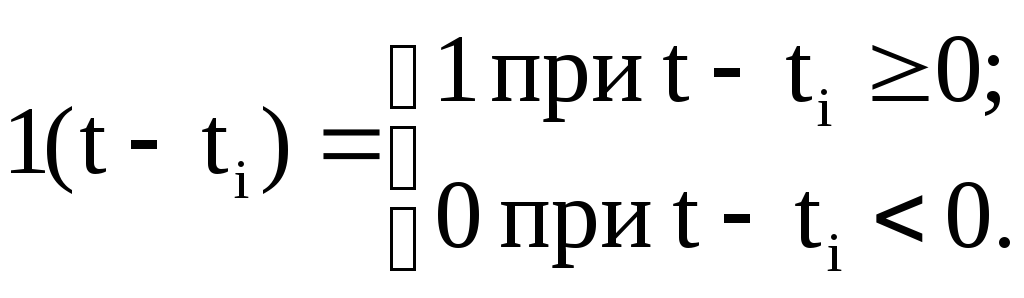
на число интервалов квантования, содержащихся в i-м уровне:

Значения x в пределах одного интервала квантования необходимо от­носить к какому-либо уровню. Очевидно, этими уровнями могут быть либо верхняя, либо нижняя граница интервала, либо середина интервала, а из рис. 4 следует, что последний способ округления наиболее рациональный, так как погрешность квантования уменьшается вдвое. Погрешность квантования в первых двух способах округления имеет максимальное значение , а при третьем способе округления , т.е. наибольшая погрешность равна половине и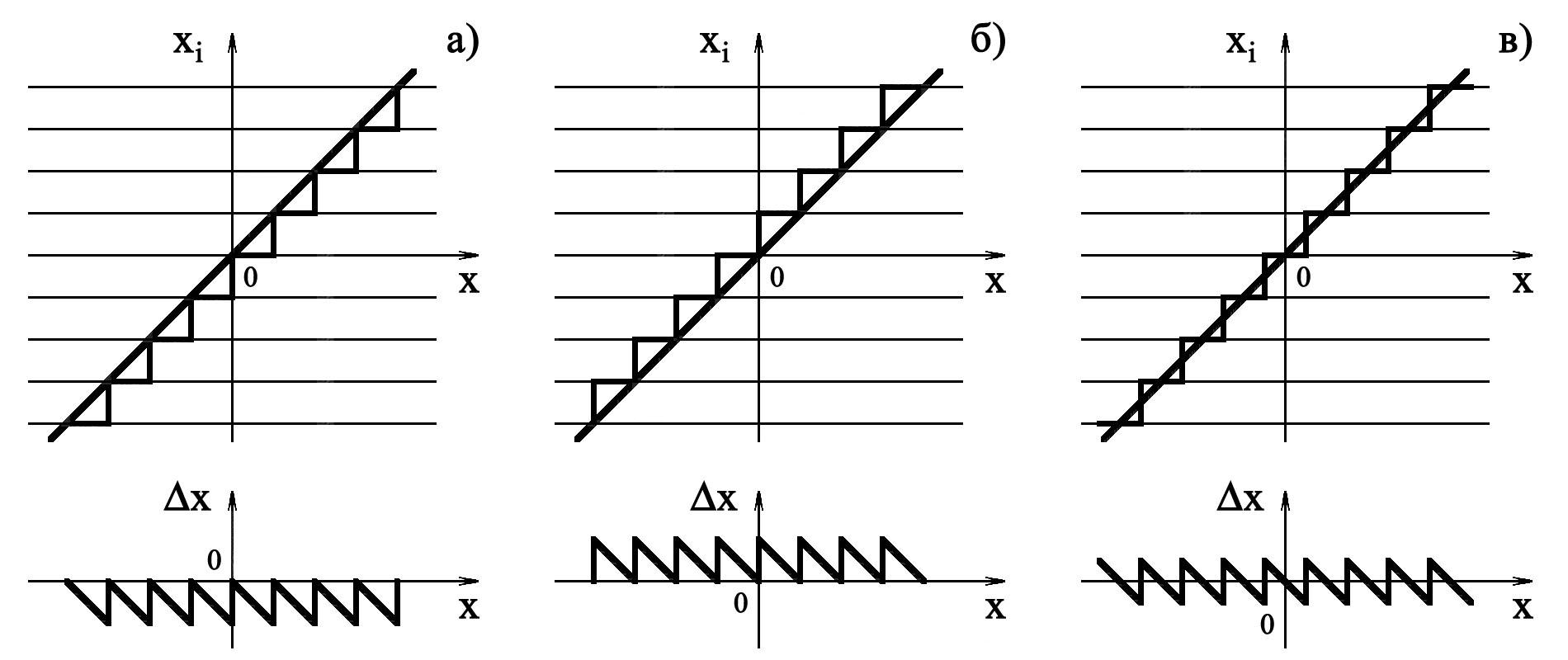нтервала квантования.

Рис. 4. Погрешность квантования по уровню:

а – при округлении по верхним границам интервала квантования;

б – при округлении по нижним границам интервала квантования;

в – при округлении по середине интервала квантования.

Так как x – случайная величина с плотностью распределения f(x), то и ∆x – также случайная величина, зависящая от x, с той же плотностью распре­деления. Ее статические характеристики следующие:

математическое ожидание

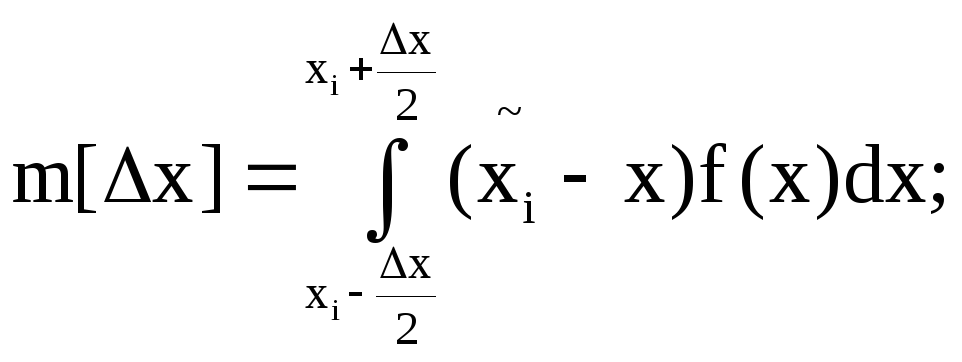
дисперсия

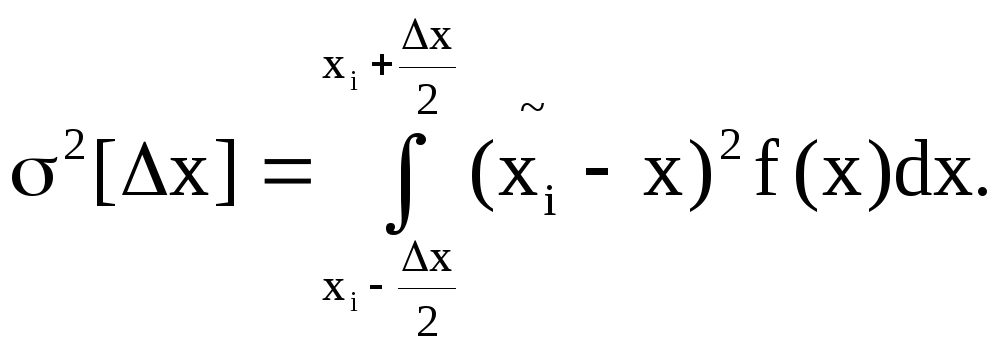
Для большого числа уровней N плотность вероятности внутри одного интер­вала квантования можно считать равномерной, тогда m[∆x]=0; ^[∆x]=∆x^/12,

а среднее квадратическое отклонение

(*)

Зная статистические характеристики погрешности квантования, можно найти число уровней квантования N при заданной погрешности. Если ∆x=(b-a)/N то, подставляя (*) в последнее выражение, получим

где – диапазон изменения значений измеряемого сигнала; N – число уровней квантования.

Дискретизацией непрерывного по времени сигнала x(t) является преоб­разование его в последовательность дискретных значений x(i·T_ц),

где (рис. 5). Временной интервалT_ц между соседними аргументами процесса называется шагом дискретизации.

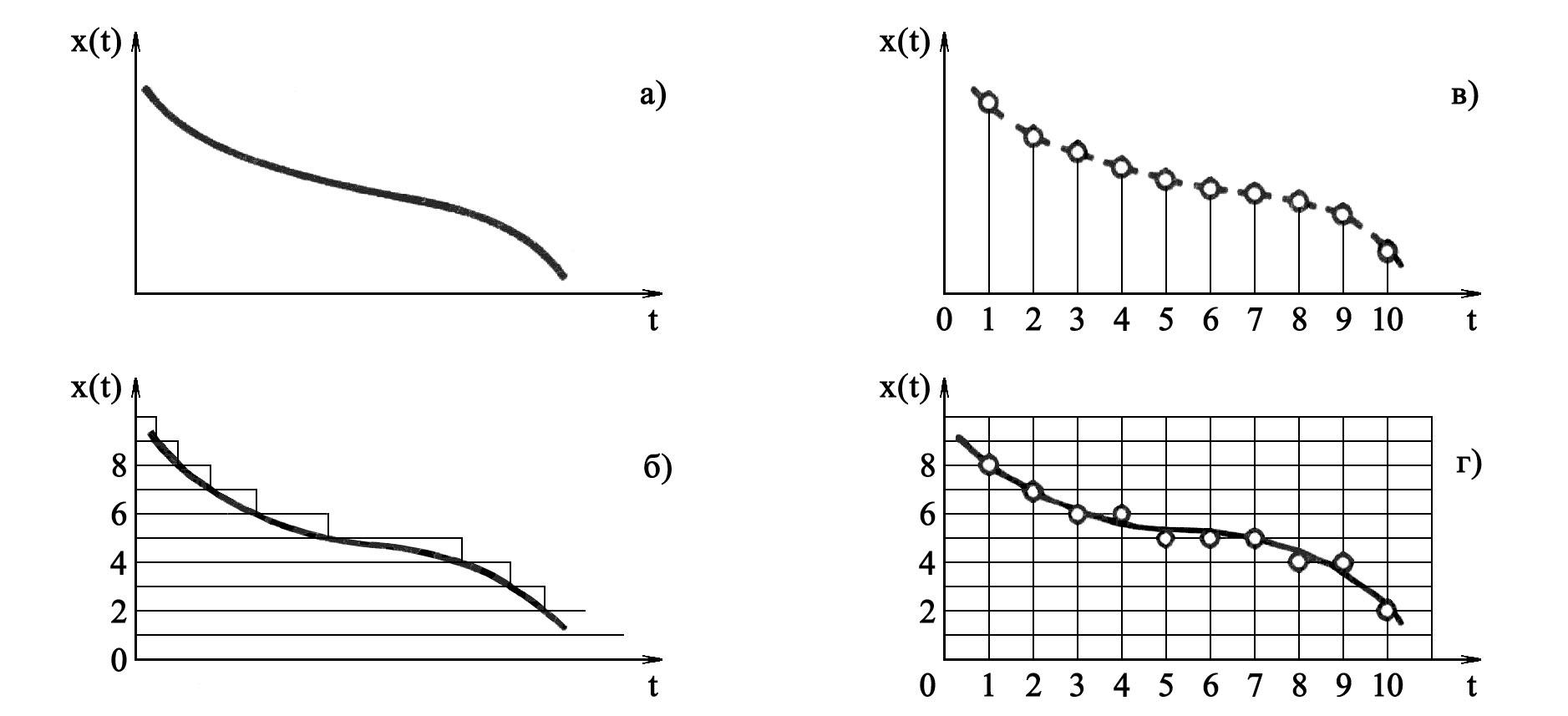Рис. 5. Виды сигналов измерительной информации:

а – аналоговый, б – квантованный, в – дискретизованный, г – цифровой.

Дискретизация процесса может быть равномерной, тогда T_ц=var. Шаг дискретизации T_ц выбирается таким образом, чтобы задача восстановления неравномерного сигнала по его заданным дискретным значениям решалась с минимальной погрешностью. Аналитически дискретный сигнал может быть представлен в виде

где δ(·) – функция Дирака.

Особый интерес представляет случай, когда дискретный сигнал про­квантован (рис. 5г), т.е. каждая его ордината x(t_i) соотнесена с числом интер­валов квантования ∆х и представлена в виде x(t_i)=N(t_i)·∆х. Тогда квантован­ный дискретный сигнал аналитически выражается как

Такой сигнал называется цифровым.