Формула Бернулли

Формулы теории вероятностей имеют смысл только в случае, когда возможно повторение испытаний достаточно большое число раз. Пусть производится пнезависимых испытаний и вероятность появления некоторого событияАв каждом из испытаний равнар = р (А) и не зависит от номера испытания. Пустьq = 1 – p, тогда вероятность того, что в п независимых испытаниях событиеАпроизойдет ровнотраз вычисляется по формуле Бернулли:

Рп(т) =  рт  qп-т.

(14)

Пример 13.Играется матч между шахматистамиXиY. Вероятность того, чтоX выиграет каждую отдельную партию равна, вероятность выигрыша партииYравна. Ничьих партий не бывает (т.е., если они происходят, то они не учитываются). Матч состоит из 6 партий. Найти вероятность выигрыша матчаX, вероятность выигрыша матчаYи вероятность ничейного исхода.

Решение.Здесь число испытанийп = 6; р = ,q = . Введем обозначения:А_i(I = 0,1,…, 6)– событие, заключающееся в том, чтоXвыигралi партий из 6. По условию задачи требуется найтир(А₄ + А₅ + А₆) = р(А₄) + р(А₅) + р(А₆) –Xвыиграл не менее четырех партий (здесь вероятность суммы равна сумме вероятностей, т.к. слагаемые в скобках – несовместимые события). Далее,

р(А₄) = р₆(4) =   = 15 =,

р(А₅) = р₆(5) =   = 6 =,

р(А₆) = р₆(6) =   = 1 =.

Тогда вероятность того, что Xвыиграет матч равна

Р(А₄ + А₅ + А₆) = =0.68.

Ничья происходит при счете ”3 -3”, т.е.

Р(А₃) = р₆(3) =   = 20 ==0.22.

Вероятность выигрыша матча Y равна

Р(А₀ + А₁ + А₂) =1 – р(А₃ + А₄ + А₅ + А₆) = 1 – 0.68 – 0.22 = 0.1.

Интересно заметить, что вероятность того, что наиболее искусный игрок не будет выявлен после шести партий не мала (0.32).

Наивероятнейшее число появления события в серии изn испытаний определяется неравенством

(15)

где p– вероятность появления события в одном испытании,q- вероятность не появления события в одном испытании.

Пример 14. В одном из учебных заведений обучается 2920 студентов. Вероятность того, что день рождения наудачу взятого по списку студента приходится на определенный день года равнаНайти наивероятнейшее число студентов, родившихся 1 января.

Решение. Имеем

следовательно,

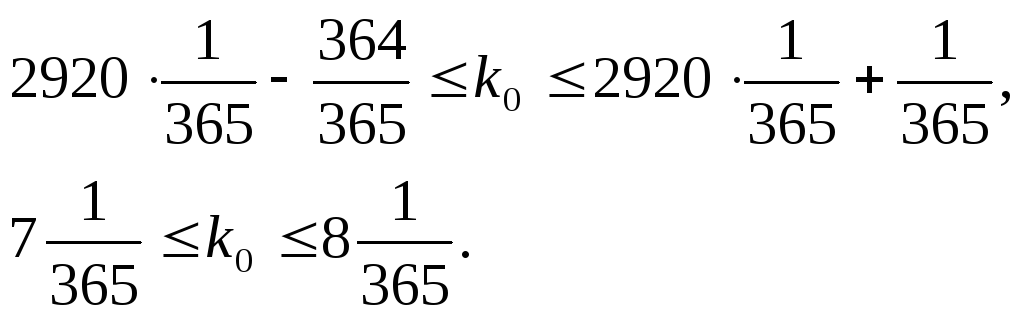
Поскольку - целое число, то= 8.

Формула Пуассона

Вычисление по формуле Бернулли (14) становятся сложными, если число испытаний п велико. Поэтому при большом числе испытаний и при малых вероятностях появления событияА (п 10, р0.1)вместо формулы Бернулли используют приближенную формулу Пуассона:

e­λ-

(16)

вероятность того, что в писпытаниях событие произойдетkраз; здесь λ =п р.

Пример 15. Прядильщица использует 10 веретен. Вероятность обрыва нити на каждом веретене равнар = 0.08. Найти вероятность того, что оборвутся ровно две нити.

Решение. Здесьq = 1 – p = 0.92. По формуле Бернулли получаем

Р₁₀(2) =  р²  q⁸ = 450.08²0.92⁸= 0.1478.

Применим формулу Пуассона:

Таким образом, даже при не больших значениях псовпадают две первых значащих цифры.

Пример 16. В банк отправлено 40000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков равна 0.0001. Найти вероятность того, при проверке будет обнаружено:

1. три ошибочно укомплектованных пакета;

2. не более трех пакетов;

3. не менее трех пакетов;

4. хотя бы один ошибочно укомплектованный пакет.

Решение. Вычислим параметрв формуле Пуассона:

1. 

2. 

3. 

4.