3. Использование факторных функциональных моделей в анализе
хозяйственной деятельности сельскохозяйственных предприятий
3.1. Использование аддитивных факторных моделей в анализе
себестоимости продукции
Общий вид аддитивных
моделей Y=X1+X2+....+Xn
или
,
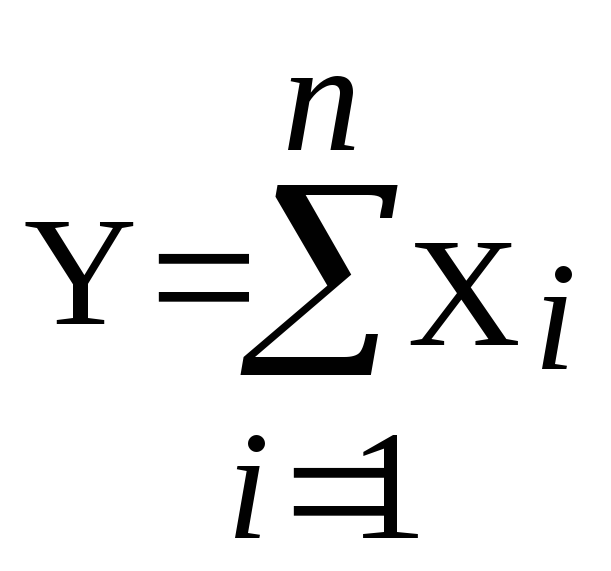где Y - результативный показатель;
X1, X2....Xn - факторы.
Результат представляет собой алгебраическую сумму факторов. Такие модели используются для анализа структурных показателей. Например, аддитивная факторная модель себестоимости молока. Себестоимость равна сумме статей затрат. Для анализа изменения себестоимости используются абсолютные и относительные отклонения анализируемого значения от базисного.
Y=Y-Y0
, Iy
=
,
где Y - фактическое значение результативного показателя;
Y0 - базисное значение результативного показателя.
Y=Y-Y0=X1-X10+X2-X20+....+Xn-Xn0=X1+X2+....+Xn,
или Y(Xi)=Xi. Изменение результативного показателя за счет i-го фактора равно изменению самого фактора Y=Y(X1)+Y(X2)+....+Y(Xn).
Аддитивные модели можно преобразовать в мультипликативную и смешанную модели.
Тогда трехфакторную аддитивную модель вида Y=X1+X2+X3 преобразуем следующим образом: умножим и разделим на один и тот же фактор:
X1+X2+X3 X1+X2+X3 X1+X2+X3
Y = ---------------- X1 = -------------- X2 = ------------- X3.
X1 X2 X3
X1+X2+X3 X1+X2+X3 X1+X2+X3
Обозначим ---------------- = K1; --------------- = K2; -------------- = K3 ,
X1 X2 X3
где К1, К2, К3 – коэффициенты, показывающие величину результативного
показателя на единицу соответствующего фактора.
Тогда получим: Y = K1X1 = K2X2 = K3X3.
Получили 3 мультипликативные модели результативного показателя. Количество моделей равно количеству факторов.
В модели Y = K1X1
X1 - изменение результативного показателя за счет первого фактора,
K1 - изменение результативного показателя за счет изменения прочих факторов.
По аналогии в других моделях:
X2, X3 - изменение результата за счет названных факторов,
K2, K3 – изменение результата за счет прочих факторов.
Индекс изменения результативного показателя
Y X1+X2+X3 X1 X2 X3
Iy = ----- = ------------------- = ------------------ + ----------------- + ----------------- =
Y0 X10+X20+X30 X10+X20+X30 X10+X20+X30 X10+X20+X30
X10 X1 X20 X2 X30 X3
= ----------------- x ----- + ------------------ x ----- + ------------------- x ----- ;
X10+X20+X30 X10 X10+X20+X30 X20 X10+X20+X30 X30
X1 X2 X3
----- = Ix1 ; ------ = Ix2 ; ----- = Ix3 - индексы изменения соответствующих
X10 X20 X30 факторов;
X10
------------------ = dx10 - удельный вес фактора X10 в сумме всех факторов
X10+X20+X30 базисного периода.
Таблица 2 - Значения результативного признака и факторов (в рублях)
|
Показатели |
Анализируемое значение |
Базисное значение |
|
РЕЗУЛЬТАТИВНЫЙ ПРИЗНАК |
|
|
|
Y – себестоимость 1 ц молока |
36.250 |
33.300 |
|
ФАКТОРЫ |
|
|
|
Х1 – оплата труда |
7.350 |
6.700 |
|
Х2 – корма |
19.700 |
18.800 |
|
Х3 – амортизация |
2.100 |
1.700 |
|
Х4 – текущий ремонт |
0.800 |
0.900 |
|
Х5 – прочие затраты |
3.200 |
2.400 |
|
Х6 – общехозяйственные и общепроизводственные затраты |
3.100 |
2.800 |
|
УДЕЛЬНЫЙ ВЕС ФАКТОРОВ В РЕЗУЛЬТАТИВНОМ ПРИЗНАКЕ |
|
|
|
dx1 – оплата труда |
0.203 |
0.201 |
|
dx2 – корма |
0.543 |
0.565 |
|
dx3 – амортизация |
0.058 |
0.051 |
|
dx4 – текущий ремонт |
0.022 |
0.027 |
|
dx5 – прочие затраты |
0.088 |
0.072 |
|
dx6 – общехозяйственные и общепроизводственные затраты |
0.086 |
0.084 |
|
ВЕЛИЧИНА РЕЗУЛЬТАТИВНОГО ПРИЗНАКА НА ЕДИНИЦУ ФАКТОРА |
|
|
|
К1 – на единицу оплаты труда |
4.932 |
4.970 |
|
К2 – на единицу корма |
1.840 |
1.771 |
|
К3 – на единицу амортизации |
17.262 |
19.588 |
|
К4 – на единицу текущего ремонта |
45.313 |
37.000 |
|
К5 – на единицу прочих затрат |
11.328 |
13.875 |
|
К6 – на единицу общехозяйственных и общепроизводственных затрат |
11.694 |
11.893 |
Тогда индекс изменения результативного показателя можно записать
Iy=Ix1 ·dx10 + Ix2 ·dx20 + Ix3 ·dx30 – смешанная факторная модель (сумма трех мультипликативных моделей).
Ix1 – измение результата (индекс его изменения) от действия первого фактора;
Ixi – изменение результата за счет действия i-го фактора;
dx10 – изменение результата (изменение индекса) за счет удельного веса первого фактора;
dxi0 – изменение результата за счет удельного веса i-го фактора.