То же в газовой (паровой) фазе:

где Ма и Мb – молекулярные массы компонентов a и b соответственно; Са – содержание компонента а в жидкой (твердой) фазе в массовых долях;

Са′ – содержание компонента а в газовой (паровой) фазе в массовых долях.

При проведении расчетов сорбционных процессов состав фаз часто выражают в относительных массовых единицах. Связь между относительным массовым составом ха ( уа ) и массовой долей Са (Са′ ) выражается сле-

дующими соотношениями:

Выражение 6.12 с учетом парциального давления компонентов и общего давления системы можно преобразовать к виду

где Ма – молекулярная масса поглощаемого компонента а; Мн – молекулярная масса не поглощаемого (инертного) компонента; ра – парциальное давление поглощаемого компонента а; Робщ – общее давление смеси.

6.1.3. Материальный баланс процессов массообмена

Рассмотрим элемент массообменного аппарата (рис. 6.3), в котором движутся потоки двух фаз: фазы Фу (например, пара) и фазы Фх (например, жидкости). Пар движется снизу вверх, жидкость – сверху вниз. Такой способ организации движения называется противоточным.

179

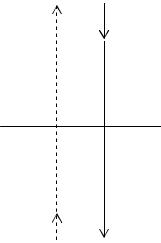
Расход поглотителя в фазе Фу составляет G кг/с, а в фазе Фх – L кг/с. Содержание распределяемого компонента в фазе Фу составляет у , а в фазе

Фх – х.

Оба этих расхода равны, поэтому можно записать уравнение материального баланса:

Находим соотношение между расходами носителей в обеих фазах:

В любом произвольном сечении элемента аппарата (например, а–а) составы фаз будут равны у и х. Составим уравнение материального ба-

ланса для части элемента аппарата, расположенной выше этого сечения:

откуда

180

Полученное уравнение называется уравнением рабочей линии, которое выражает зависимость между неравновесными составами фаз (у, х) в любом сечении массообменного аппарата.

Решая совместно уравнения (6.17) и (6.19), после простых преобразований получим выражение

Это выражение является уравнением прямой, проходящей через точки А( х1 , у1 ) и В( х2 , у2 ) (см. рис. 6.1). В данном случае в соответствии с усло-

вием поставленной задачи рабочая линия расположена выше линии равновесия, т.к. рабочие концентрации распределяемого компонента в фазе Фу выше равновесных концентраций и он переходит из фазы Фу в фазу Фх.

При обратной постановке задачи, когда распределяемый компонент переходит из фазы Фх в фазу Фу, рабочие концентрации в фазе Фу ниже равновесных. В этом случае рабочая линия А′В′ расположена ниже линии равновесия.

6.1.4. Уравнение массопередачи

Количество вещества, переходящего из фазы, где его содержание выше равновесного, в фазу, где содержание этого вещества ниже равновесного, пропорционально степени отклонения от равновесия: разности концентраций – рабочей концентрации вещества в одной из фаз и равновесной концентрации в ней этого вещества, которая называется движущей силой процесса, а также пропорционально площади соприкосновения фаз и продолжительности процесса массообмена:

где М – количество вещества, перешедшего из одной фазы в другую, кг; К – коэффициент пропорциональности, называемый коэффициентом массопередачи; – движущая сила процесса массопередачи; F – поверхность соприкосновения (контакта) фаз, м2; τ – продолжительность процесса массопередачи, с.

Размерность коэффициента массопередачи зависит от размерности движущей силы процесса, которая выражается в виде разностей объемных

181