
Климанов Дозиметрическое планирование лучевой 2007
.pdf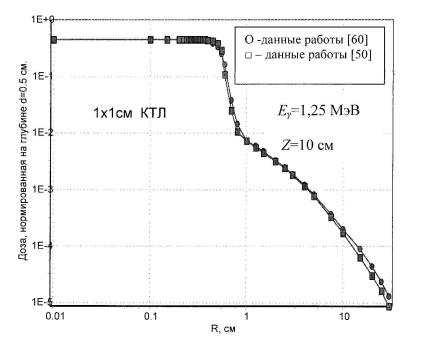
Рис. 5.7. Зависимость ядра КТЛ размером 1х1 см2, выраженного в единицах относительной дозы (нормировка на дозу на оси КТЛ на глубине 0.5 см), от расстояния до оси КТЛ
3.4 Основные приближения модельных алгоритмов
Как ясно из предыдущего изложения, модельные алгоритмы основываются на использовании понятий ядер элементарных источников, описывающих распределение поглощенной энергии в единице объема среды. Для воды это распределение совпадает с дозовым распределением, поэтому для краткости будем в этом случае называть их дозовыми ядрами. Отметим следующие упрощающие расчет допущения, которые принимаются в модельных методах расчета относительно дозовых ядер:
1. В первую очередь постулируется пространственная инвариантность дозовых ядер. Однако вблизи границы тела пациента это не выполняется. Принимается, что дозовые ядра не зависят от направления падения излучения на фантом или пациента. Считается, что излучение падает нормально на поверхность, тогда как на самом деле пучки являются расходящимися.
161

2. Для убыстрения расчетов обычно используются ядра, усредненные по спектру падающего излучения. В то же время энергетический спектр не одинаков на разных расстояниях от оси пучка и на разных глубинах в фантоме.
Практически во всех коммерческих системах планирования не учитывается зависимость дозовых ядер от атомного номера среды и используются данные для воды.
Эти приближения естественно сказываются на точности расчета доз с помощью модельных алгоритмов. Для уменьшения возникающей погрешности в алгоритмы вводятся различные поправочные факторы, которые часто основаны на использовании экспериментальных данных.
4.Метод дифференциального тонкого луча
4.1.Общая постановка
Влитературе этот метод часто называют методом свертки/суперпозиции. Точное выражение для расчета дозы в произ-
вольной точке r |
с помощью ядра ДТЛ имеет вид: |
|
|
||||||
r |
1 |
∫dΩ∫dΕ∫d |
3 r′ |
r′ |
r′ |
r |
r |
r′ r |
|
D(r) = |
r |
r |
µ(E,r )ψ(r ,E,Ω)Кдл (z,Ε,Ω, ρ,r ,r ), |
||||||
|
ρ(r ) |
|
|
|
|
|
|
|
|
(1)
где Ψ – флюенс энергии первичного излучения; z – атомный номер среды; ρ – плотность среды.
С учетом упрощающих допущений (1, 2 и 4) выражение (1) переходит в следующее:
D(rr) = ρ(1rr) ∫dE∫d 3 rr′µ(Ε,rr′) Ψ(rr′, Ε) Kдл (E,rr′− rr) . (2)
При проведении дальнейших преобразований уравнения (2) принято использовать понятия интегральной термы T(r) и диффе-
ренциальной термы TE (rr).
Под дифференциальной термой понимается энергия, освобождаемая в единице массы первичными фотонами с энергией Е. Связь между флюенсом энергии первичных фотонов и дифференциальной термой следующая:
162

|
TE (rr) = |
µ(E,r r ) |
Ψ(rr,E) . |
(3) |
|
|
|
|
(r ) |
|
|
Интегральная терма равна интегралу от TE (r) по энергии. |
|
||||
С учетом (3) выражение (2) приобретает вид: |
|
||||
D(rr) = |
1r |
∫dE∫d 3 rr TE (rr′) ρ(rr′) Kдл (E, rr′− rr) . |
(4) |
||
|
ρ(r ) |
|
|
|
|
Переформулируем проблему, чтобы избежать лучевого анализа и интегрирования по энергии. Введем ядро, усредненное по спектру падающего излучения:
|
|
(rr) = |
Ψ(1rr ) |
∑Ψi Kдл (Ei ,rr) , |
(5) |
|
|
K |
|||||
|
|
|
о |
|
i |
|
где Ψi = ∫Ψ(E,rro )dE ; rr0 |
– радиус вектор поверхности облучае- |
|||||
∆Ei
мого объекта; Ψ(rro ) – интегральный энергетический флюенс. Тогда уравнение (5) переходит:
r |
F(r ) |
∫d |
3 r′ |
r′ |
r′ |
|
r′ |
r |
|
|
|
||||||||
D(r ) = |
r |
r |
T(r ) ρ(r ) K (r |
− r ) , |
(6) |
||||
|
ρ(r ) |
|
|
|
|
|
|
|
|
где F(r ) – поправочный фактор на «ужестчение» спектра фотонов
с увеличением глубины.
Величина интегральной термы в геометрии облучения при дистанционной лучевой терапии определяется из выражения:
|
|
|
|
2 |
r |
|
|
|
r |
r |
|
µ(r ) |
r |
∫µ(l)dl] , |
|
||
|
|
|
|
|||||
T (r ) = |
|
|
|
r |
Ψ(ro ) exp[− |
(7) |
||
|
||||||||
|
ro |
|
ρ(r ) |
rr |
→rr |
|
||
|
|
|
|
|
|
o |
|
|
где µ(rr) – усредненный по спектру линейный коэффициент ослабления фотонов, который определяется как:
|
(rr) = |
Ψ(1rr ) |
∑Ψi µ(Ei ,rr) . |
(8) |
µ |
||||
|
|
o |
i |
|
Фактор ужестчения спектра можно найти из выражения:
|
∫ |
dΕ |
∫ |
d |
3 v′ |
w |
v′ |
w |
v′ |
v |
|
|||
F(rv) = |
r |
TE |
(r ) Kдл (E, r |
− r ) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
, |
(9) |
|||
|
|
|
|
v |
|
r |
|
w |
v |
v |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∫d 3 r ′ T w (r ′) K |
|
(r |
′− r ) |
|
|
|
||||||
163
где верхний индекс w означает, что значения функций рассчитываются для воды.
В последних системах планирования проводится также коррекция на дивергенцию ядра и на внеосевое смягчение спектра первичных фотонов. Удобным приемом для учета многих поправочных факторов является введение коефициента коррекции через ссылочное поле:
F |
= |
Доза,измереннаявводномфантоме . |
(10) |
||||||
сп |
|
v |
v |
|
|
w |
v |
v |
|
|
′) K |
|
|||||||
|
|
∫d 3 r |
′ T w (r |
|
(r |
′− r ) |
|
||
4.2. Аналитическая аппроксимация ядра ДТЛ в воде
Анализируя результаты расчетов ядра ДТЛ в воде для спектров тормозного излучения 4 MВ, 6 MВ, 10 MВ, 15 MВ и 24 MВ автор работы [51] нашел, что зависимость ядра от переменной r можно приближенно описать формулой:
К |
дл |
(r,θ) = (A e−aθ r + B |
θ |
e−bθ r )/r 2 |
, |
(11) |
|
θ |
|
|
|
где Аθ, аθ, Вθ, bθ – эмпирические параметры, зависящие от угла θ и спектра фотонов. Значения этих параметров были определены методом наименьших квадратов [51].
Важным обстоятельством является также то, что первый член выражения (11), согласно [51], описывает, главным образом, первичную энергию, передаваемую в воде как первичную дозу, а второй член энергию рассеянных фотонов, передаваемую как дозу рассеянного излучения. Если это утверждение справедливо, то интеграл от первого члена
Ι = ∫∫∫ |
Аθ |
e−aθ r r 2 |
sin θ dr dθ dϕ = 2π∫ |
Aθ |
sin θ dθ (12) |
2 |
|
||||
|
r |
|
aθ |
||
должен равняться средней доле энергии, поглощаемой в среде при акте взаимодействия первичного фотона. Результаты расчета интеграла (12) хорошо совпадают с теорией для 4 MВ, 6,0 MВ и 10 MВ тормозных фотонов и хуже для 15 MВ и 24 MВ. Вместе с тем, полная поглощенная энергия хорошо сохраняется.
164
4.3.Аналитическая аппроксимация ядра ДТЛ
вгетерогенной среде
Под гетерогенными средами в этом разделе понимаются среды с переменной плотностью, но водоэквивалентные по эффективному атомному номеру. Такое упрощение, примененное к практическим задачам дозиметрического планирования лучевой терапии, не очень существенно отражается на погрешности расчета дозы для высокоэнергетичных пучков. Так, например, в работе [52] были выполнены расчеты доз в гетерогенном антропоморфном фантоме с точным заданием химического состава отдельных органов и скелета. Второй расчет был проведен для такого же фантома, но с заменой конкретных веществ на водоэквивалентные с измененной (эквивалентной) плотностью. Различие в двух расчетах доз для внутритканевых точек оказалась меньше 0,4 %.
Следующее упрощение состоит в пространственном масштабировании ядра ДТЛ в соответствии с распределением плотности между точкой взаимодействия первичного фотона и точкой детектирования (расчета). Это соответствует концепции прямолинейности распространения энергии, освобождаемой при взаимодействии первичного фотона, от точки взаимодействия к точке детектирования. Строго говоря, это неправильно, особенно на больших расстояниях. Здесь значительный вклад в дозу вносит многократно рассеянное излучение. Но для однократно рассеянного излучения такая концепция выполняется вполне удовлетворительно.
Концепция прямолинейности, примененная к выражению (11), позволяет формально рассматривать поглощенную энергию, как создаваемую двумя разными частицами с линейными коэффициентами ослабления аθ и bθ . Физические частицы, представленные в (11) первым членом, являются, главным образом, электронами, образующимися при взаимодействии первичного фотона. Частицы, представленные в (11) вторым членом, являются фотонами. Поэтому естественно предположить [38], что коэффициент ослабления аθ первого члена в гомогенной водоэквивалентной среде, но с другой плотностью (ρm≠1 г/см3), пропорционален отношению тормозной способности среды к тормозной способности воды. В свою очередь, коэффициент ослабления bθ второго члена в такой же среде пропорционален отношению коэффициентов ослабления рассеянных фотонов в среде и в воде.
165

В этой аппроксимации ядро ДТЛ в произвольной водоэквивалентной по атомному номеру среде (ρm≠1) описывается уравнением:
K |
дл |
(r,θ) = [S |
m,w |
A |
e−aθ (ρm ρw ) Sm,w r +µ |
m,w |
B |
θ |
× |
|
|
θ |
|
(13) |
|||||
×e−bθ ( ρm ρw ) µm,w r ]/ r 2 |
|
|
|
|
|||||
|
|
|
|
|
|||||
где: ρm и ρw – плотности среды и воды; Sm,w – отношение массовых тормозных способностей электронов для среды и воды; µm,w – отношение массовых коэффициентов ослабления рассеянных фотонов для среды и воды.
Массовая тормозная способность приблизительно пропорциональна электронной плотности. Это же справедливо для массового коэффициента ослабления рассеянных фотонов, так как основным процессом взаимодействия в рассматриваемой проблеме является комптоновское рассеяние. Так как отношение плотностей, помноженное на отношение числа электронов в единице массы, равно отношению числа электронов на единицу объема, то обозначив его через η, упростим выражение (13):
K |
дл |
(r,θ) = η [A e−a |
θ η r + B |
θ |
e−b |
θ η r ]/ r 2 . |
(14) |
|
θ |
|
|
|
|
Отсюда получим обобщение для гетерогенной среды, считая, что
η = η(r,θ,ϕ) |
(15) |
является пространственно зависимой. Окончательно получаем:
K (r,θ,ϕ) = η(r,θ,ϕ){Aθ exp[−aθ ∫r |
η(t,θ,ϕ)dt] + |
|
0 |
(16) |
|
+ Bθ exp[−bθ ∫r η(t,θ,ϕ)dt]}/r 2 . |
||
|
||
0 |
|
4.4. Алгоритм “Разложение на конусы”
Выражение (6) позволяет, в принципе, провести прямой численный расчет дозового распределения в 3-мерной пространственной
сетке. Ядро К(rv′− rv) при этом берется в форме (16), r ′ иденти-
фицируется как начало координат и r задается как (r, θ, φ). Однако такой подход встречает две серьезные проблемы.
Первая связана с очень большой трудоемкостью расчета. Обозначим число интервалов сетки по каждой из осей в декартовой системе
166
координат через N. Линейные интегралы в показателях в формуле (16) должны оцениваться для всех комбинаций точек рассеивания и детектирования. Следовательно, для каждой расчетной точки нужно рассмотреть N3 точек рассеивания. Число точек расчета тоже равняется N3. Каждый расчет при этом потребует N операций. Таким образом, полное время расчета будет пропорционально N7.
Вторая трудность связана с сильным градиентом ядра (16) по переменной r на пробеге электрона (рис.5.3) и особенностью 1/r2 в нуле. Дело в том, что при численном расчете требуется дискретизация уравнения (6). Желаемое пространственное разрешение при дозиметрическом планировании находится в диапазоне 0,1 ÷1,0 см.
На таком расстоянии терма изменяется несильно. Трудности возникают с ядром ДТЛ в силу отмеченных его особенностей. Прямое суммирование значений ядра в аналитической форме (16), используя в качестве значений r расстояние между центрами рассеивающей и расчетной ячеек (вокселей), приводит к существенным погрешностям и становится невозможным, когда рассеивающий воксель совпадает с расчетным. Предложенный в работе [51] алгоритм “Разложение на конусы” решает отмеченные трудности.
Рассмотрим дискретную сферическую координатную систему, т.е. систему вокселей в виде конических сегментов с телесным углом Ωmn вокруг θm и φn и толщиной ∆r. Пространство, покрытое отдельным вокселем определяется как:
rl −1 ≤ r ≤ rl ;
θ,ϕ Ωmn .
Определим поток волновой энергии (энергии первичных электронов и рассеянных фотонов) Rmn(rl), испускаемой в конус Ωmn из
рассеивающего объема dV в начале координат (0) и следующей
через сферическую поверхность rl. Будем исходить из аналогии с формулой, связывающей поглощаемую в объеме ∆V энергию фотонов ∆Е с энергетическим флюенсом ψ :
∆Ε = µen (E) ψ(E) ∆V , |
(18) |
где µen (E) – линейный коэффициент поглощения энергии фотонов.
Поглощаемая энергия здесь определяется формулой (16), где роль линейных коэффициентов играют параметры aθ и bθ. Отсюда находим следующее уравнение для Rmn :
167
Rmn (rl ) = T (0v) ρ(0v) dV ∫∫ |
1 |
{ |
Aθ |
exp[−aθ ∫r η(t,θ,ϕ)dt] + |
|
||
2 |
aθ |
|
|||||
|
|
Ωmn |
r |
|
0 |
(19) |
|
|
Bθ |
exp[−bθ ∫r η(t,θ,ϕ)dt]} r 2 sin(θ) dθ dϕ. |
|||||
+ |
|
||||||
bθ |
|
||||||
|
0 |
|
|
|
|
|
|
Для краткости дальнейшие преобразования проведем с первым слагаемым в (19). Переходя к кусочно-постоянным значениям η(r, θ, φ), Аθ и аθ внутри конусных ячеек и численно оценивая интегралы, получаем дискретную версию первого слагаемого в выражении
(19):
v
Rmnp (rl ) =T(0)
где ∆r = rl − rl −1 ;
ρ(0v) dV Ωmn |
Am exp(−am ∑ηlmn ∆r) , (20) |
|
|
|
l |
|
am |
i=1 |
Rmnp – поток энергии, переносимой первичными
электронами, т.е. электронами, образующимися при первом взаимодействии фотонов.
Так как поглощенная доза определяется как поглощенная ( часто употребляется термин “переданная”) энергия на единицу массы, то первичная доза вблизи поверхности rl от волновой энергии, освобождаемой в начале координат в направлении Ωmn будет равна:
D p |
(r ) = |
η |
|
|
a |
|
R p |
|
(r ) dr |
. |
(21) |
||
|
lmn |
|
|
m |
mn |
|
l |
||||||
mn |
l |
|
ρ |
lmn |
r |
2 Ω |
mn |
dr |
|
|
|||
|
|
|
|
|
l |
|
|
|
|
||||
Доза, обусловленная рассеянными фотонами, рассчитывается аналогично с заменой Аm , аm на Bm, bm. Для определения полной дозы необходимо выполнить интегрирование всей энергии, освобождаемой рассеивающими вокселями.
Естественный выбор координатной системы при дозиметрическом планировании – декартовая система, т.е. все величины, являются средними в вокселях ∆х ∆y ∆z . Чтобы перевести в эту сис-
тему уравнения (20,21), применим аппроксимационный алгоритм “Разложение на конусы”.
Основное приближение этого алгоритма заключается в том, что вся энергия, освобождаемая внутри коаксиальных конусов с телесным углом Ωmn из объемных элементов, расположенных на оси,
168

прямолинейно распространяется, ослабляется и поглощается в элементах на этой же оси.
Декартовые воксели, близко расположенные к рассеивающей точке, являются более широкими, чем сферические воксели. Один декартовый воксель может здесь покрывать более одного конического сегмента (рис. 5.8). В таком случае точность не теряется по сравнению с прямолинейной аппроксимацией.
Рис. 5.8. Схема покрытия сферическим вокселем декартовых вокселей (к прямолинейной аппроксимации поглощения энергии )
Однако с увеличением расстояния один сферический воксель может покрывать уже несколько декартовых вокселей (см. рис. 5.8). Тогда при принятом приближении часть декартовых вокселей получит слишком много “впрыскиваемой ” энергии, в то время как другие не получат совсем. Однако это компенсируется покрытием этих декартовых вокселей другими (соседними) коллапсными “конусными” линиями, что позволяет сохранить в целом освобождаемую энергию.
Чтобы применить данный алгоритм к дискретной декартовой системе, расчетный объем покрывается сеткой линий, вдоль которых распространяется волновая энергия, освобождаемая первичными фотонами, падающими на облучаемый объект (рис. 5.9). Каждая линия делится на шаги ∆r, так чтобы плотность и терма могли считаться постоянными внутри каждого интервала. Чтобы избежать флуктуаций, линии должны быть определены так, чтобы воксели проходились один раз по каждому направлению θm, φm.
169

Рис.5.9. Пример сетки линий (плоский вариант), вдоль которых распространяется волновая энергия
По соображениям размерности линиям присваиваются бесконечно малые поперечные сечения d2u. Тогда объемный рассеиваю-
щий элемент dV уравнения (21) представляется как d 2u dr и объемный детектирующий элемент r 2 Ωmn dr уравнения (22) заме-
няется на d 2u dr . Волновая первичная энергия, освобожденная из сегмента I вдоль такой линии (r меняется от ri-1 до ri) в конус с телесным углом Ωmn , будет равна (см. уравнение (20)):
|
|
|
|
|
|
|
|
|
|
|
ri |
A |
|
|
∆R p |
(r ) = T ρ |
i |
Ω |
mn |
d 2u |
m |
e−am ηi (ri −t ) dt = |
|
||||||
|
|
|||||||||||||
mn |
|
i |
|
i |
|
|
|
|
r∫ |
am |
|
|||
|
|
|
|
|
|
|
|
|
|
|
(22) |
|||
|
|
|
|
|
|
|
|
|
|
|
i −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= T ρ |
i |
Ω |
mn |
d 2u |
Am |
(1 −e−am ηi ∆r ), |
|
|||||||
|
|
|||||||||||||
i |
|
|
|
|
|
ηi am2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
170 |
|
|
|
|
