Кашурников Сверхтекучест и бозе-конденсация 2008

может быть выше, чем оценка (1.87) для трехмерной системы.

81

2. Низкоразмерная сверхтекучесть

переходов. Бозонная модель Хаббарда

Исследования сверхтекучести и бозе-конденсата в дальнейшем коснулись проблем протекания сверхтекучего гелия в пористых каналах, натекания на поверхности, и привели к пониманию возможности существования фазовых переходов в квантовых системах пониженной размерности даже при нулевой температуре.

На эксперименте наблюдали скачки химического потенциала при натекании очередного слоя сверхтекучего гелия на графойл (скол поверхности графита) [56 – 58], при протекании по углеродным нанотрубкам [59].

Почему могут быть фазовые переходы в одномерных квантовых системах? Существует доказательство Ландау [60] об отсутствии таких переходов в классической одномерной системе, и объясняется оно ростом тепловых флуктуаций и потерей устойчивости упорядоченной фазы. Однако для квантовой ситуации фазовое пространство имеет еще одну размерность – ось

Имеется небольшое число точно решенных одномерных квантовых моделей. Среди них – фермионная модель Хаббарда, ферро- и антиферромагнитные спиновые модели, модель Кондо [62]. Модель с бозонными степенями свободы точно не решается, но она интересна для исследования проблем бозе-конденсации и сверхтекучести.

82

Модель Бозе – Хаббарда [63] была развита для описания фазовых переходов сверхтекучесть – изолятор и сверхтекучесть – бозе стекло, в таких системах, как сверхтекучий гелий, квантовые спиновые стекла, вихревая решетка в ВТСП, система джозефсоновских контактов и т п.

любая модель типа Хаббарда, гамильтониан (2.1) коммутирует с оператором полного числа частиц, так что исследовать• данную модель можно при конкретном бозонном заполнении ç.

В отсутствие взаимодействия на соседних узлах (Q = /) модель (2.1) имеет богатую фазовую диаграмму [63] и имеет фазовый переход из сверхтекучего состояния в бозе-стекло или моттовский

сердцевинами” [64]. Эта модель обладает смешанной статистикой

– фермионы на одном узле и бозоны (симметричная волновая функция) на разных местах решетки. Кроме того, эта модель

83

Если ослабить запрет на числаsзаполнения,# + например допустить двойное заполнение узлов ( y ), то получаем первую из моделей soft-core-бозонов – так называемую редуцированную бозонную модель Хаббарда. Дальнейшее смягчение запрета на числа заполнения приведет в конце концов к полной бозонной модели (2.1) [64].

Таким образом, модель Бозе – Хаббарда имеет большую область применимости для самых разнообразных квантовых систем с сильными корреляциями.

84

2.2.Фазовые диаграммы "сверхтекучесть – бозе-стекло – моттовский изолятор". Связь с другими моделями

Рассмотрим подробнее полную модель (2.1), оставив только

место.

85

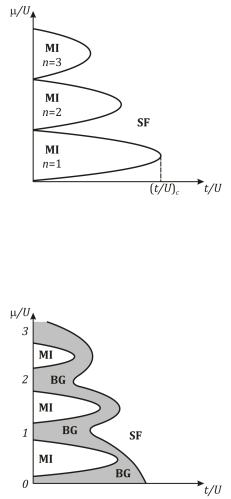
Рис. 2.1. Фазовая диаграмма9 = / “сверхтекучесть (SF) – моттовский изолятор (MI)” при для бозоной модели Хаббарда в отсутствии беспорядка

Рис. 2.2. Фазовая диаграмма “сверхтекучесть9 = / (SF) – бозе-стекло (BG) – моттовский изолятор (MI)” при для бозонной моделиºХаббарда в

присутствии слабого андерсоновского беспорядка

в состояние с ¹= /, и _^ = /) при увеличении параметра ! ¨. В соизмеримом случае возможна также ситуация, когда фазы

"моттовский изолятор – бозе-стекло – сверхтекучесть"! ¨

реализуются последовательно с изменением параметра (рис. 2.2).

Покажем качественно, как можно объяснить наличие различных фазовых состояний в модели Бозе – Хаббарда.

Изучим сначала модель без примесей при Q = /, т.е.! =оставим/ взаимодействие только на узлах. Положим для начала , т.е. «выключим» перескок, тогда бозоны находятся на узлах решетки и локализованы. Энергию одного бозона как функцию плотности в

¨

этом случае легко рассчитать прямо из гамильтониана:

S's) = WŠs b + s's W )( '+(F)

Также несложно рассчитать энергию при добавлении одной

частицы в систему или удалении одной частицы¨ из системы:

S's b ) = WŠ's b ) b + s's b )A

S's W ) = WŠ's W ) b ¨+ 's W )'s W +)( '+(f)

Рассмотрим эти величины как функции химического потенциала (рис. 2.3).

Рис. 2.3. Зависимость энергии одной частицы от химического потенциала

87

Рис. 2.4. Числа заполнения в зависимости от химического потенциала при нулевой амплитуде перескока

Внутри каждого интервала имеется энергетическая щель в спектре, не позволяющая увеличивать число частиц, пока не

Это состояние моттовского изолятора, названного по аналогии с состоянием изолятора в ферми-системах. Частицы локализованы,

!ТеперьÐ / «включим» движение, т.е. положим амплитуду перескока , тогда переходы между моттовскими областями’s ’Š

«размоются», щели немного уменьшаться, и производнаяŠ Š уже не будет равна бесконечности в области между M и ‚ (рис. 2.5).

Рис. 2.5. Числа заполнения в зависимости от химического потенциала при ненулевой амплитуде перескока

щелью в спектре возбуждений. Заметим, что моттовскаяß = ’s ’Šобласть характеризуется бесконечной жесткостью , а сверхтекучая – конечным значением этой величины.

При определенном критическом значении '! ¨)C эти зависимости сливаются, и происходит фазовый переход из моттовского изолятора вs сверхтекучее состояние при сохранении числа заполнения . Это – переход при соизмеримом заполнении, кратном числу узлов. Именно такие фазовые переходы наблюдали

89

при натекании пленки сверхтекучего гелия на скол графита –

графойл [56].

2.3.Определение критических точек. Численный спектроскопический анализ. Сверхтоковые состояния. Идентификация сверхтоковых и фононных возбуждений в одномерной разупорядоченной системе

Рассмотрим бозонную модель Хаббарда (2.1) и ее модификации. Аналитический расчет этой модели сильно затруднен, поэтому изучим систему численно, методом точной диагонализации

гамильтоновой матрицы с расчетом нижних возбужденных состояний.

В одномерной ситуации проблема сверхтекучести в достаточно большой, но конечной системе может быть исследована из анализа нижних возбужденных состояний. Такой анализ называется спектральным. Действительно, добавочную энергию, связанную со сверхтоковым состоянием c топологическим