Кашурников Сверхтекучест и бозе-конденсация 2008

Рис. 1.9. Спектр возбуждений взаимодействующего бозе-газа: а) слабое взаимодействие; б) сильное взаимодействие. Штриховая прямая

скорость движения жидкости

Из вида спектра возбуждений видно, что локальных минимумов на нем нет, так как смене линейной на квадратичную зависимость соответствует только точка перегиба (рис. 1.9, а). Однако это верно лишь для слабонеидеального газа. Для реальных жидкостей при

Спектр возбуждений, показанный на рис. 1.9, наблюдался в экспериментах Хеншоу и Вудса по рассеянию медленных нейтронов [15].

Пользуясь законом дисперсии (1.35), получим вклад в

Вернемся теперь к слабонеидеальному газу и закону дисперсии (1.33). Подставляя в (1.26) выражение (1.10), имеем для среднего числа частиц

32

температуре.

1.6.Сверхтекучесть. Двухжидкостная модель. Критерий сверхтекучести Ландау. Термодинамика сверхтекучей жидкости. Второй звук

При низких температурах наиболее интересным свойством бозежидкости является свойство сверхтекучести, одним из проявлений которого является способность жидкости протекать по капиллярным трубкам без трения (Л.Д. Ландау, 1941 [2]). Покажем, что это свойство следует из особенностей рассмотренного выше спектра возбуждений, показанного на рис. 1.9, б.

Рассмотрим]Æбозе-жидкость при 9 = /, текущую по капилляру со скоростью . Если между жидкостью и стенками капилляра имеется трение, это может привести к увлечению жидкости стенками капилляра и, соответственно, к появлению элементарных возбуждений и диссипации энергии.

33

элементарного возбуждения, поэтому критерий Ландау (1.43) означает, что сверхтекучее движение может иметь место только, если скорость жидкости меньше скорости элементарного возбуждения в точках, удовлетворяющих (1.44). Как видно из рис. 1.9, б, критическая точка лежит правее ротонного минимума. Несложно оценить из спектра (1.35), что скорость сверхтекучего движения должна быть

Рассмотрим качественную картину движения бозе-жидкости, когда выполняется критерий Ландау. При нулевой температуре 9возбужденияÐ / отсутствуют, и движение сверхтекучее. Как только , появляются возбуждения, которые сталкиваются со стенками капилляра и участвуют в вязком движении жидкости с диссипацией энергии. В таком движении участвует лишь часть массы жидкости. Дело в том, что движение газа возбуждений ]относительно жидкости сопровождается переносом массы. Пусть

– относительная скорость такого движения. Тогда импульс газа

возбуждений в единице объема’ ]Æ Žs ’

ÑÒ = ‘r Æs …S¦ W Æ]‰ '+>) ÍÉž$ W * ‘ ŽS '+>) ( ' (F )

Так как импульс пропорционален скорости, то происходит перенос массы (он и есть коэффициент пропорциональности). Оставшаяся часть массы жидкости будет по-прежнему двигаться без диссипации. Таким образом, как и было9 Ðпредложено/ в двухжидкостной модели, бозе-жидкость при представляет собой смесь двух жидкостей – сверхтекучей и нормальной, движущихся без трения друг относительно друга. Из (1.46) можно получить фононную и ротонную части нормальной плотности,

*'+>) 9

Оставшаяся часть плотности _^ соответствует сверхтекучему движению. Итак, в сверхтекучей жидкости имеет место

двухжидкостное движение с плотностью_ = _ b _ ( ' (F2)

` ^

35

Следует отметить важное свойство: если жидкость помещена во вращающийся цилиндр, то нормальная часть будет увлечена стенками и станет вращаться с ним. Напротив, сверхтекучая часть будет покоиться, ее нельзя привести во вращение, так как

движение сверхтекучей компоненты всегда потенциально. Это свойство можно записать математически:6ÕÖ ]Æ = /& ' (FO)

^

где ]Æ^ – скорость сверхтекучей компоненты.

Двухкомпонентная гидродинамика бозе-жидкости во многом отличается от обычной гидродинамики. В бозе-жидкости могут происходить колебания двух различных типов с разными скоростями. Колебания первого типа – обычный звук, или первый

1.7.Квантование циркуляции и топологические вихри. Эффект Хесса – Фейрбенка

Богатство физических явлений в этой квантовой системе далеко не исчерпывается упомянутыми выше эффектами. Достаточно подробное объяснение многих экспериментов с точки зрения двухжидкостной модели см., например, в [16]. Здесь не были рассмотрены эффекты – аналоги эффекта Джозефсона в сверхпроводниках, эксперименты в сверхжидкостной аэродинамической трубе, экспериментальное наблюдение

36

вихрей, особенности протекания по тонким капиллярам, распространение звука и др.

Рассмотрим интересное явление квантования циркуляции в сверхтекучем гелии и важные физические следствия из него.

она постоянна и будем пренебрегать ее флуктуациями. Тогда

оператор плотности потока массы

a^ = + ÚhÁÛh b h' ÛhÁ)Ü = ghg ݤ( ' (f+)

Пусть гелий-II заполняет кольцевую область – пространство между двумя цилиндрами (рис. 1.10).

Рис. 1.10. СверхтекучаяÞ жидкость в кольцевой (многосвязной области). Контур полностью находится в сверхтекучей жидкости

Рассмотрим циркуляцию сверхтекучей скорости:

ß = à ]Æ^ ’áÆA

37

Þ

Для окружности (см. рис. 1.10) легко получить, что

ß = Ç 'â¤)ã( ' (ff)

Для однозначности волновой функции при полном обходе контура

экспериментально наблюдал Вайен [17].

Выражение для квантования циркуляции (1.56) справедливо дляÞ любого контура, который можно непрерывно деформировать в , не выходя за границы жидкости. Кольцевая область представляет собой пример многосвязной области, т.е. любого «отверстия» в массиве сверхтекучей жидкости, куда она не может проникать. Такие области могут быть созданы двумя способами. Во-первых, они могут искусственно создаваться твердыми поверхностями, т.е. конфигурацией сосудов для гелия. Во-вторых, при вращении гелия в сверхтекучей жидкости спонтанно могут возникнуть цилиндрические отверстия, вокруг которых возникают устойчивые потоки. В этих случаях фактически можно наблюдать возникновение вихревых линий (нитей) (рис. 1.11), подобных вихрям в сверхпроводниках второго рода.

38

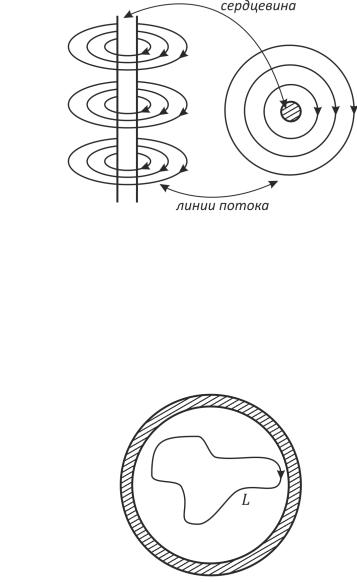
Рис. 1.11. Вихревая нить в гелии-II

Согласно двухжидкостной модели, сверхтекучую компоненту невозможно привести во вращение, так как сверхтекучий поток

должен характеризоваться условием6ÕÖ ]Æ = отсутствия/( ' (f,)вихрей

^

Рис. 1.12. СверхтекучаяÞ жидкость в цилиндрическом сосуде. Контур в односвязной области можно свести в точку

39

Действительно, рассмотрим заключенный в сосуд гелий-II

Здесь учтена теорема Стокса при переходе из контурного в поверхностный интеграл и использовано условие (1.57). Это означает, что циркуляция по любому контуру в сплошной сверхтекучей жидкости равна нулю. Любой контур в сплошной, односвязной жидкости можно стянуть в точку, т.е. условие (1.58) справедливо для любой точки жидкости. Но тогда, ]согласноÆ = / контурному интегралу в (1.58), в каждой точке скорость ^ , и вращение невозможно. Эксперимент Андроникашвили [12] с вращающимися дисками также указывал на это, дисками увлекалась только нормальная компонента. Но в экспериментах Осборна [18] вращался цилиндрический сосуд с гелием-II, и было замечено, что мениск у стенок сосуда имеет ту же форму, как и у обыкновенной несверхтекучей жидкости, вращающейся как целое. Таким образом, и нормальная, и сверхтекучая компоненты гелия вращались с одной и той же угловой скоростью.

Можно было бы заключить, что сверхтекучести во вращающемся гелии нет. Для проверки этого Андроникашвили и Каверкин провели эксперимент по эффекту фонтанирования во вращающемся гелии-II [19] и показали, что эффект сохраняется. Только при достаточно большой критической скорости (согласно критерию Ландау) сверхтекучесть разрушается.

Альтернативное, и как оказалось, правильное объяснение состоит в том, что при вращении сверхтекучая компонента пронизана рядом вихревых нитей (рис. 1.13).

40