Загребаев Методы матпрограммирования 2007

3.3. Минимизация функций без ограничений (безусловная минимизация)

В настоящем разделе будут изучены методы нахождения минимума функции многих переменных f (x1 , K, x n ) по всему про-

странству R n , т.е. при условии, что при поиске экстремума каждая из переменных xi может принимать значения от –∞ до +∞. Допустим, что f (x) обладает единственным минимумом и что все част-

ные производные, по крайней мере первого порядка, существуют при любых значениях x .

Прежде всего, рассмотрим методы отыскания экстремума функций без ограничений, а затем перейдем к более трудной задаче отыскания экстремума с ограничениями. Это необходимо потому, что задача оптимизации с ограничениями часто решается путем преобразования ее к задаче оптимизации без ограничений.

Все методы безусловной минимизации сводятся к нахождению последовательности точек x0 , x1 , K, x n , значения функции в кото-

Эти методы называются методами спуска (или релаксационными методами).

При получении таких последовательностей точек в задачах с ограничениями, прежде всего, необходимо выбрать начальную точку x0 , удовлетворяющую всем ограничениям.

В задаче без ограничений можно в качестве x0 взять любую точку. При этом, конечно, нужно использовать любую имеющуюся информацию о поведении функции f (x) с тем, чтобы выбрать x0

не слишком далеко от точки минимума.

После того, как какая-то точка выбрана, необходимо:

1)выбрать направление, вдоль которого предполагается расположить следующую точку;

2)решить, какой величины шаг должен быть сделан в выбранном направлении.

При любом методе спуска последовательность точек выглядит так:

181

шага. Изменяя процедуру выбора Sk и λk , можно получать раз-

личные методы спуска.

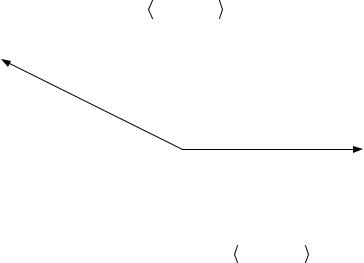
Для задач без ограничений любое направление является возможным, однако не все направления приемлемы. Приемлемым называется такое направление Sk , для которого выполняется условие

геометрически представленное на следующем рисунке.

S k

f (xk )

xk

Действительно, для достаточно малых λk можно написать разложение функции в ряд Тейлора

если этот член< 0, то f ( xk +λSk )< f ( xk )

Все методы спуска можно разбить на две группы:

1)прямые методы или методы нулевого порядка – методы, использующие только значения функций;

2)методы первого порядка – методы, использующие, кроме того, первые производные;

3)методы второго порядка – методы, использующие кроме первых производных еще и вторые производные.

Производные могут вычисляться аналитически или численно. Вообще говоря, методы третьей группы при наименьшем числе шагов приводят к точкам, достаточно близким к точкам минимума. Это, однако, не означает, что они являются наиболее эффективны-

182

ми методами в отношении расхода машинного времени, необходимого для решения задачи. Иногда функция f (x) представляет со-

бой настолько сложную функцию, что ее первая или вторая производные не могут быть получены аналитически, а их численные приближения оказываются очень грубыми. Кроме того, вычисление этих производных может потребовать больше машинного времени, чем вычисление значений функции в необходимом для метода нулевого порядка числе точек.

Таким образом, невозможно выделить какой-либо метод, пригодный в любом случае. Для отыскания метода, наиболее пригодного для оптимизации заданной функции, необходимы опыт, интуиция и, может быть, предварительные исследования.

3.3.1.Методы нулевого порядка

3.3.1.1.Метод покоординатного спуска

Наиболее простым способом определения направления спуска

является выбор в качестве ˆk одного из координатных векторов

S

e1 , e2 , K, en .

вектор, у которого i-я компонента равна 1, а остальные – нулю. Иначе говоря, в методе покоординатного спуска на каждой итерации поиск точки с меньшим значением функции осуществляется изменением одной компоненты вектора x при неизменных остальных.

Существует несколько вариантов покоординатного спуска. Мы рассмотрим некоторые из них.

Покоординатный спуск с удвоением шага (первый вариант)

Опишем первый цикл метода, состоящий из n итераций. Пусть заданы точка x0 и шаг λ0 .

183

В точке x0 выбирают начальное направление S1 = e1 и выбирают величину шага λ1 способом удвоения. Этот способ состоит в следующем:

удвоения шага продолжают до тех пор, пока убывание функции не прекратится;

3) если f (x0 + λ1S1 ) ≥ f (x0 ) , то выбирают λ1 = λ1 / 2 и переходят к п. 2.

Шаг дробят до тех пор, пока он не уменьшится до некоторой малой величины ε. Это означает, что в данном направлении функция не убывает.

Если в направлении e1 функция f (x) убывает, то фиксируют λ1 и переходят к следующей итерации. В противном случае выбирают направление S1 = −e1 и снова определяют величину шага λ1

способом удвоения. Если и в данном направлении функция не убывает, то фиксируют неудачный поиск в данном направлении; в качестве значения λ1 берут начальное значение шага λ0 и переходят

к следующей итерации.

процесс, как на первой итерации.

Цикл заканчивается при k = n , т.е. после того, как пройдет поиск по всем n направлениям S1 = ±e1 , S2 = ±e2 , K, S n = ±en .

Если поиск по всем n направлениям оказался неудачным, то процесс прекращается: x* = xn .

В противном случае начинается новый цикл: Sn+1 = e1 и т.д.

184

Покоординатный спуск с удвоением шага (второй вариант)

Каждый цикл этого метода характеризуется тем, что величина шага λ в течение всех n итераций цикла остается постоянной. Предполагается, что в результате завершения предыдущего цикла получена некоторая величина шага λ.

Рассмотрим i-ю итерацию цикла (1 ≤ i ≤ n ), которая состоит в следующем:

1) если

то x не меняют (полагают x = x ) и переходят к следующей итерации.

Таким образом, осуществляется n итераций цикла.

Если неравенства (3.6) и (3.9) имеют место для всех 1 ≤ i ≤ n , то уменьшают величину λ, полагая, как правило, λ = λ / 2 и переходят к следующему циклу, то есть повторяют все процедуры предыдущего цикла, но уже с шагом, уменьшенным в два раза.

Если неравенство (3.6) или (3.9) имеют место не для всех i, то шаг λ не дробится.

Процесс заканчивается, когда величина шага становится меньше заданной величины ε, определяющей требуемую точность вычисления точки минимума.

185

Покоординатный спуск с одномерной минимизацией

Цикл данного метода опять содержит n итераций. Каждая итерация состоит в поиске минимума функции вдоль одной из координат при неизменных остальных. Поиск минимума осуществляется одним из методов одномерной минимизации. Изобразим алгоритм в виде блок-схемы, представленной на рис. 3.12.

Вход

Ввод исходных данных

ε i , ε 2 , n, x 0 , f ( x 0 ), k = 0

Выход

Рис. 3.12. Блок-схема алгоритма метода покоординатного спуска

Недостаток метода покоординатного спуска (всех его вариантов) заключается в том, что он может «застревать», т.е. он может

186

остановиться вдали от точки минимума и не обеспечить дальнейшего улучшения. Такая ситуация может возникнуть, если поверхности уровня целевой функции обладают острыми углами или очень изогнуты. На рис. 3.13, приведенном ниже и отображающем расположение линий уровня f (x) = C , представлен пример такой

ситуации.

Рис. 3.13. Линии уровня в методе покоординатного спуска

Если процесс решения привел в точку x 0 , то каким бы малым ни брать шаг в направлении x1 или x2 , нельзя получить уменьше-

ние значения функции. Метод «застревает» в точке x 0 . Рассмотрим несколько примеров применения метода покоорди-

натного спуска.

Задача 1. Построить блок-схему метода покоординатного спуска с удвоением шага (второй вариант).

Блок-схема метода покоординатного спуска с удвоением шага при поиске минимуму по каждой координате приведена на рис. 3.14. При этом использованы следующие обозначения:

k – номер цикла;

i – номер (внутри цикла) итерации движения по i-му направлению ( i =1, n );

j – счетчик неудачных шагов, когда x не меняется; x – текущее значение аргумента (без индекса).

187

Схему решения задачи можно представить в виде следующей последовательности действий.

Цикл k =1 .

189

Соответственно: итерация i =1:

Линии уровня, соответствующие рассматриваемой функции приведены ниже:

190