Загребаев Методы матпрограммирования 2007

величин xi* , y*j на шаге ( l +1 ). Эти значения рассчитываются, с

Оценки цены игры на ( l +1 )-шаге вычисляются по формуле:

которая в скалярной форме имеет вид

i=1 j=1

3. Итерационный процесс заканчивается, когда значение функции (4.6) становится достаточно малым, т.е. когда выполняется соотношение:

251

Рис. 4.1. Структурная схема алгоритма фон Неймана

252

4.1.4.Математическое программирование

втеории биматричных игр

4.1.4.1.Биматричные игры. Основные теоретические сведения

Матричная игра является антагонистической игрой [23], т.е. игрой двух лиц с нулевой суммой. Однако на практике часто встречаются такие ситуации, когда интересы сторон не являются прямо противоположными. В этом случае игра имеет произвольную сумму, отличную от нуля, и является неантагонистической.

Конечную игру двух игроков с произвольной суммой можно описать парой матриц – поэтому она называется биматричной.

Биматричная игра определяется следующим образом. Два игрока обозначены буквами A и B . Игрок A имеет в своем распоряжении m чистых стратегий, а B – n чистых стратегий. Если A выбирает свою i -ю чистую стратегию, а B – j -ю чистую страте-

гию, то выигрыш игрока A есть aij , а выигрыш игрока B есть bij .

Определим матрицы A1 и B1 как матрицы размером m × n , (i, j) элементы которых есть aij и bij . Игра полностью определена, ко-

гда заданы матрицы выигрышей A1 и B1 .

Смешанная стратегия игрока A есть столбец X из неотрицательных элементов xi , которые представляют собой относитель-

ную частоту, с которой A будет выбирать свою i -ю чистую стратегию. Таким образом,

Аналогично смешанная стратегия игрока B есть столбец Y , неотрицательные элементы y j которого в сумме равны 1. Если A и

B всегда выбирают чистую стратегию случайным образом в соответствии с распределением вероятностей, заданным векторами X и Y , то ожидаемые выигрыши игроков A и B соответственно

253

Вэтих соотношениях выражение в скобках означает скалярное произведение соответствующих векторов.

Вотличие от матричных игр, где существует единственный критерий оптимальности поведения игроков, в неантагонистических играх вообще и в биматричных в частности, таких критериев не-

сколько. Различают ситуации равновесия по Нэшу, сильно равновесные ситуации и ситуации, оптимальные по Парето. Каждый из этих подходов к оценке оптимальности поведения игроков имеет свои достоинства и свои недостатки [13].

Далее пойдет речь только о ситуациях равновесия по Нэшу. Ситуация равновесия в игре есть пара смешанных стратегий

Иными словами, ситуация равновесия – такая ситуация, отклонение от которой одного из игроков не может увеличить его выигрыш.

Следует отметить, что ситуаций равновесия в биматричной игре может быть несколько. Причем в различных ситуациях равновесия выигрыши неодинаковы, а множество ситуаций равновесия прямоугольно.

Теорема Нэша гарантирует существование ситуаций равновесия в биматричных играх [28], но не дает никаких средств для их нахождения.

Наиболее эффективным из всех известных алгоритмов для практических вычислений ситуации равновесия является алгоритм, предложенный Лемке и Хоусоном в 1963 г. [67], [44]. По своей сути этот алгоритм тесно связан с методами нелинейного программирования, изложенными в разделе 3 настоящего издания. Следует особо подчеркнуть то обстоятельство, что данный алгоритм может быть без особых затруднений реализован на ЭВМ.

Докажем, прежде всего две теоремы, на основании которых можно сформулировать постановку задачи.

254

Теорема 4.1. Ситуация ( X 0 ,Y 0 ) является ситуацией равновесия в биматричной игре с матрицами выигрышей A1 и B1 в том и только в том случае, когда

где Lm и Ln – векторы размерности m и n соответственно, со-

ставленные из единиц (знаки неравенств используются для покоординатного сравнения векторов).

Доказательство. Пусть ( X 0 ,Y 0 ) – ситуация равновесия, т.е.

Возьмем в качестве X и Y векторы, у которых одна из компонент равна единице, а остальные – нулю. Получим m + n соотношений

является произвольным вектором. Представим его в базисе единичных векторов f1 , f2 ,..., fm следующим образом:

что и требовалось доказать.

255

Применение методов математического программирования возможно, если существует некоторое допустимое множество, соответствующее ограничениям на аргументы целевой функции, в качестве которых рассматриваются компоненты смешанных стратегий игроков. При решении биматричных игр такое множество значений аргументов строится с помощью простой операции: перехода к платежным матрицам A и B , элементы которых – положительные числа.

Рассмотрим матрицы

единиц. Вследствие процедуры (4.24) изменяются и условия (4.20). Теорема 4.2. Ситуация

256

т.е.

Учитывая, что EY 0 = Lm а ( X 0 , Lm ) =1 , получим

Это соотношение можно использовать при вычислении цены игры для участника с платежной матрицей A1 .

Поскольку Y * ≥ 0 , т.е. (Y * , Ln ) ≥ 0 , неравенство

Используя полученный в начале доказательства результат, придем к неравенству

По аналогии доказывается справедливость соотношения

Согласно теореме 4.1 выполнение этих условий является необходимым и достаточным, чтобы утверждать, что пара ( X 0 ,Y 0 ) –

ситуация равновесия. Теорема доказана.

257

матрицы B , есть эквивалентная форма записи условий теоремы.

4.1.4.2. Нахождение ситуации равновесия в биматричных играх

Доказав теоремы 4.1 и 4.2, получили критерий, с помощью которого удобно определять, является ли пара ( X 0 ,Y 0 ) ситуацией

равновесия.

Действительно, если исходить только из определения ситуации равновесия, то для проверки пары ( X 0 ,Y 0 ) необходимо переби-

рать все векторы X и Y из множества смешанных стратегий. Сделать это невозможно. Вот почему потребовалось найти необходимое и достаточное условие, в записи которого фигурируют только векторы X 0 и Y 0 .

Постановка задачи нахождения ситуации равновесия. Пусть

A и B > 0 .

Задача состоит в том, чтобы найти пару ( X * ,Y * ) , для которой

Будем называть любую пару ( X * ,Y * ) ситуацией равновесия.

Допустимое множество для поиска смешанных стратегий игрока 1 определяется в соответствии с соотношениями (4.40) и (4.41) следующим образом:

т.е. Χ состоит из векторов X , для которых

258

Конец вектора X лежит на границе множества Χ , если хотя бы одно из этих соотношений является равенством.

Аналогично можно рассмотреть множество

Граница множества Υ состоит из точек, удовлетворяющих хотя

Легко убедиться, что Χ и Υ – многогранники, у которых соответственно имеются m и n бесконечных ребер.

* * *

Пример 4.1. Рассмотрим игру с матрицами выигрышей

Выберем d = 2 , получим матрицы

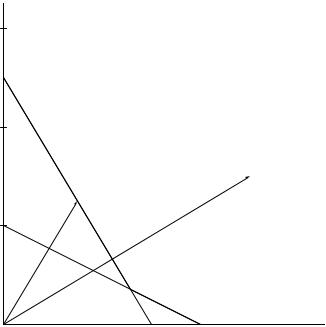
Множество Υ , показанное на рис. 4.2, определяется следующими соотношениями:

0,25y1 + 0,5y2 −1 ≥ 0;

0,34 y1 + 0,2 y2 −1 ≥ 0;

y1 ≥ 0, y2 ≥ 0,

259

а множество Χ , показанное на рис. 4.3, – соотношениями:

0,5x1 + 0,33x2 −1 ≥ 0;0,2x1 + y2 −1 ≥ 0;x1 ≥ 0, x2 ≥ 0.

Y2

6

4

Yвн

Yгр

2

Рис. 4.2. Множество Υ : Yвн – внутренняя точка; Yгр – точка на границе

Заметим, что здесь и в дальнейшем используется важное предположение, сделанное при постановке задачи:

A > 0 и B > 0 .

Именно это условие гарантирует существование выпуклых открытых многогранников Χ и Υ .

260