
Загребаев Методы матпрограммирования 2007
.pdf

|
|
− f ( |
|
) |
|
k |
x |
||
y |
g(x) = 0
pk Sk |
xk |
X
Рис. 3.30. Определение направления в методе проекции градиента
В зависимости от способа выбора шага λk можно получить раз-
личные варианты метода проекции градиента (можно использовать одномерную минимизацию и т.д.).
Условием прекращения процесса является условие pk = xk , которое является необходимым и достаточным условием того, что точка xk – точка минимума (доказывается с помощью специальной теоремы).
Например, pk = xk , если f ( xk ) = 0 , так как тогда yk = xk , и нет перемещения из точки xk . Аналогичная ситуация возникает,
если xk лежит на границе и градиент ортогонален границе допустимой области (рис. 3.31).
− f ( x )
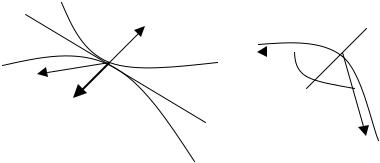
Рис. 3.31. Направление градиента совпадает с направлением градиента к границе допустимой области
Для того, чтобы найти проекцию точки yk на множество X , необходимо решить задачу минимизации квадратичной функции
232















 f
f