Емелянов Фундаменталные симметрии 2008

Для ненулевых xνxλ тензор cμνλ симметричен по индексам μ и

ν. Это тривиально показать, используя тот факт, что ν и λ – «слепые» переменные, и при суммировании можно обозначить νλ через λν:

cμνλ xν xλ = cμλν xλ xν ,

Теперь мы имеем форму εμ (x), с которой можно производить из-

менение масштаба метрики.

Если подставить общее решение для εμ (x) в первоначальное уравнение для εμ (x) :

то можно получить ограничения на коэффициенты bμν и cμνλ . Сначала найдем

∂νεμ (x) = ∂ν (aμ + bμρxρ + cμρβxρxβ ) =

= ∂ν (bμρxρ + cμρβxρxβ ) = bμρδρν + cμρβδρνxβ + cμρβxρδρν =

(1.294)

= bμν + (cμνρ + cμρν )xρ = bμν + 2cμνρxρ.

Подставляя ∂νεμ (x) в (1.289), получаем

bμν + 2cμνρxρ +bνμ + 2cνμρxρ = D2 bλλημν + D4 cλρλ xρημν.

(1.295)

Сравнивая коэффициенты при xρ в обеих частях (1.295), получаем следующие ограничения на bμν и cμνλ :

Запишем bμν в виде

92

ственно, с лоренцевскими преобразованиями и масштабными преобразованиями:

Таким образом, при общем конформном преобразовании

93

специальные конформные преобразования

Если теория симметрична относительно таких преобразований, то с этой симметрией должны быть ассоциированы сохраняющиеся токи. Это так называемые дилатонные токи. Дилатонный ток – общее свойство теории, включающей гравитационные эффекты, он связан со скалярным полем – дилатоном.

Обратимся теперь к обсуждению CPT как другой фундаментальной симметрии квантовой теории поля.

94

Глава 2

CPT КАК ФУНДАМЕНТАЛЬНАЯ СИММЕТРИЯ

2.1. Введение

Представление о CPT-симметрии (C – зарядовое сопряжение, P – пространственная инверсия, T – обращение времени) как о симметрии релятивистской квантовой теории поля возникло в работе Г. Людерса, в которой он утверждал, что зарядовое сопряжение и пространственная инверсия подразумевают одинаковые ограничения на форму гамильтониана, описывающего взаимодействия. Поэтому CPT-симметрия имеет более фундаментальный базис, чем C, P или T. В. Паули наиболее прозрачно сформулировал CPT-симметрию в контексте тех условий, которым должны удовлетворять гамильтонианы или лагранжианы. О формулировке Паули CPT-симметрии говорят как о «лагранжевой CPT-теореме». Р. Иост предложил общее доказательство CPT-симметрии, основанное на том, что пространственно-временная инверсия связана с тождественностью в комплексной группе Лоренца, однако эта инверсия не связана с тождественностью для вещественной группы Лоренца. Анализ Иоста называют «аксиоматической CPT-теоремой». Швингер обсуждал CPT и теоремы о спине и статистике с точки зрения его принципа дифференциального действия.

Учебники по квантовой теории поля выводят CPT-теорему путем вычисления каждой симметрии и рассмотрения их произведения. Это, вообще говоря, правильный подход. Однако надо иметь в виду, что каждое C-, P-, T-преобразование может иметь произвольную фазу, поскольку они не связаны с тождественным преобразованием, в то время как CPT, связанное с тождественным преобразованием, произвольной фазы содержать не может. Весьма интересно проследить, почему CPT фундаментальна, в отличие от симметрий C, P и T. Как будет видно, CPT фундаментальна потому, что она связана с лоренц-инвариантностью.

95

2.2.Представления вещественной и комплексной групп Лоренца

Ключевым аргументом при обсуждении CPT-инвариантности является утверждение о том, что связанная компонента комплексной группы Лоренца L(C), которая является сама по себе ком-

плексной группой Лоренца L+ (C ) , включает пространственно-

временную инверсию. Для того чтобы получить и пояснить это свойство, обратимся к группе Лоренца.

Вещественную группу Лоренца можно рассматривать как груп-

Можно проверить, что это условие эквивалентно утверждению о том, что Лоренц-преобразование сохраняет скалярное произведе-

ренца распадается, в зависимости от знака детерминанта Λ и знака Λ00 , на четыре несвязанные компоненты L↑+ , L↓+ , L↑− , L↓− . Очевидно, что только первая из них является группой, поскольку только

Нам нужно также рассмотреть комплексную группу Лоренца – группу комплексных 4 ×4 матриц, удовлетворяющих соотношению (2.1). Для комплексной группы Лоренца знак детерминанта

нельзя изменить непрерывным образом, однако матрица (−1) ока-

96

зывается связанной с единичным элементом, поэтому в этом случае имеется уже две несвязанных компоненты. Наиболее просто найти непрерывное семейство комплексных лоренцевских преобразова-

ний, связывающих матрицы 1 и (−1), можно путем рассмотрения накрывающих групп вещественных и комплексных групп Лоренца.

Хорошо известно, что состояние спина 1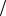2 преобразуется при вращении на угол θ с фазой θ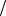2 , а не с фазой θ, как для скалярного состояния. Поэтому вращение на 2π изменяет фазу спинового состояния (12) , хотя такое вращение должно быть эквивалентным

тождественному вращению. Итак, (1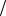2) спиновое состояние не

преобразуется как истинное представление группы вращений, оно преобразуется с точностью до фазы. Идея накрывающей группы состоит в том, чтобы найти более широкую группу, чьи представления являлись бы истинными представлениями, без дополнительных фаз. Для группы вращений накрывающей группой является

группа SU (2) – группа 2×2 унитарных комплексных матриц с единичным детерминантом. Для связанной компоненты группы

где A SL(2, C) , а звездочка означает комплексное сопряжение. Можно ввести скалярное произведение этих представлений, используя 2×2 антисимметричный символ εαβ Леви-Чивиты для

«неточечных» спиноров и εαβ – для «точечных» спиноров. Счита-

ем, что ε12 =1 и ε12 =1 . Каждое представление SL(2,C) имеет вид спинора с k «неточечными» и l «точечными» индексами и пре-

97

образующееся, согласно (2.2) и (2.3). Это представление путем свертки с ε вполне приводимо, поэтому следует считать, что не-

приводимыми представлениями SL(2,C) являются представления с k симметризованными «неточечными» и l симметризованными «точечными» индексами. Каждый индекс соответствует спину 1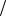2 , поэтому эти спиноры имеют спин k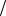2 и l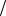2 относительно группы SU (2) SU (2) , которая возникает при выборе групп, чьи гене-

раторы J ±iK , где J – генераторы вращений вещественной группы Лоренца и K – генераторы «чистых» сдвигов.

Будем считать, что матрицы Паули имеют по одному «точечно-

det X = x2 . Вспомнив, что матрицы SL(2,C) имеют детерминант,

равный единице, обнаруживаем, что X ′ = AXA+ – эрмитова и является лоренцевским преобразованием x. Матрицы A и (−A) относятся к одному и тому же лоренцевскому преобразованию. Таким образом, группа SL(2,C) накрывает дважды связанную компо-

ненту группы Лоренца.

Для покрытия комплексной группы Лоренца допустим существование двух независимых SL(2,C) матриц, введя их так, чтобы

X ′ = AXB+ . При этом X ′ уже не будет эрмитовой, но будет попрежнему иметь ту же метрическую длину в пространстве Минковского. Таким образом, накрывающей группой комплексной

группы Лоренца L+ (C ) является SL(2,C )×SL(2,C ) . Так как

теперь в нашем распоряжении имеется две независимые матрицы A и B, мы можем добиться превращения x → −x или выбором A =1 , B = −1 или A = −1, B =1 . При этом можно непрерывным образом

98

индексов симметризован. φ(k ,l) ( x) преобразуется как неприводи-

мое представление группы SL(2,C) , описанное выше. Будем использовать в качестве накрывающей группы группу Пуанкаре, поэтому в (a, Λ) заменим Λ L↑+ величиной A SL(2, C) . Тогда на

поле φ(k ,l) ( x) Пуанкаре-преобразование действует следующим

образом:

U (a, A)φ(k ,l ) ( x)U (a, A)+ =

(2.5)

= S(k ,l) (Λ)(−1) φ(k ,l) (Λx + a).

В аргументе поля в правой части соотношения (2.5) заменим Λ

писать Λ вместо Λ( A) или Λ( A, B) в обоих случаях. Возвращаясь к соотношению (2.5), заметим, что в единственном случае, когда нам потребуется конкретная форма S(k ,l ) ( A, B), Λ L+ (C ) порождает пространственно-временную инверсию. В этом случае S(k ,l ) ( A, B) является диагональной фазой. Таким образом, кон-

кретную форму S(k ,l) знать необязательно. По этой причине будем опускать индексы, относящиеся к матрицам S(k ,l) , а также индексы, относящиеся к полю φ(k ,l ) ( x) . Предположим, что вакуум 0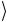 инвариантен относительно Пуанкаре преобразования

Мы могли бы ограничиться скалярными полями, чтобы избежать усложненных обозначений. Однако для рассмотрения общего

100