|
|
x1 |
x2 |
x3 |
x4 |
|
|
x5 |
|
x6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
000 |
001 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
02 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
2 |
0 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
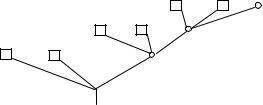
Рис. 11.19. Неполное кодовое дерево
При использовании произвольного алфавита кодировки ( D 2 ) процедура Хаффмана предполагает на первом шаге объединение
m0 сообщений с наименьшими вероятностями и D на последующих шагах.
|
Число m0 находится из условия |
|
|
|
|
2 m0 |
D; |
|
|
|
|
|
|
M m0 |
a, |
|
|
|
|
|
D 1 |
|
|
|
|
где a – целое положительное число.
7.3. При применении процедуры Шеннона – Фано целесообразно первоначальное множество расположить в порядке убывания вероятностей и именно в такой последовательности пытаться проводить разбиения на три примерно равновероятных группы. Как показывает практика построения кодов, это обеспечивает наибольшую эффективность кодирования, так как в каждой группе будут фигурировать сообщения с равновеликими вероятностями.
Что касается процедуры Хаффмана, то в ней все шаги строго регламентированы и никаких неоднозначностей кодирования нет. Произвольное присвоение символов алфавита кодировки различным ветвям дерева не нарушает общую структуру оптимального кода.
8.1. Для применения процедуры Хаффмана необходимо построить множество, которое является декартовым произведением мно-
281
жеств U 3 , и найти соответствующее распределение вероятностей
(рис. 11.20)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p( 3 ) p( |
|
) p( ) p( |
2 |
) p( |
) . |
|
|
1 |
2 |
3 |
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
3 |
|
|
p( 3 ) |
Код |
|
|
|
1, M |
|
|
|
|
|
|
1 |
|
000 |
|
1/27 |
1011 |
Источник |
|
|
|
|
|
|
1 2 3 ... ... |
|
|
|
2 |
|
001 |
|
2/27 |
1000 |
инфор- |
|
|
|
|
|
|
|
|
3 |
|
010 |
|
2/27 |
1001 |
мации |
{0,1} |
|
|
|
|
|
|
|
|
|
4 |
|
011 |
|
4/27 |
11 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
100 |
|
2/27 |
1010 |
|
|
|
|
|
6 |
|
101 |
|
4/27 |
010 |
|
|
|
|
|
7 |
|
110 |
|
4/27 |
011 |
|
|
|
|
|
8 |
|
111 |
|
8/27 |
00 |
Рис. 11.20. Схема решения задачи для D 2
8.2. Элементы решения задачи приведены на рис. 11.21.
|
|
i |
1, M |
|
3 |
|
|
|
|
000 |
|
|
1 |
|
Источник |
|
|
1 2 3 ... ... |
2 |
|
001 |
инфор- |
|
3 |
|
010 |
мации |
{0,1} |
|
|
|
|
011 |
|
4 |
|
|
|
|
|
5 |
|
100 |
|
|
6 |
|
101 |
|
|
7 |
|
110 |
|
|
8 |
|
111 |
Рис. 11.21. Схема решения задачи для
p( 3 ) |
Код |
|
|
|
1/64 |
201 |
3/64 |
21 |
3/64 |
22 |
9/64 |
10 |
3/64 |
200 |
9/64 |
11 |
9/64 |
12 |
27/64 |
0 |
D 3
8.3. Процедура асимптотически эффективного кодирования состоит из следующих шагов:
– находим наибольшее M число последовательностей T , удовлетворяющее условиям
M 2 [ H (U ) ] ;
J ( ) [H (U ) ];
– из условия Dn M 1 определяем длину кодовых слов как наименьшее большее целое
Идея кодирования состоит в том, что M последовательностей из букв представляются различными кодовыми словами одина-
ковой длины n , а все остальные последовательности – одним и
тем же кодовым словом. Возникающая при этом вероятность неоднозначного кодирования равна вероятности появления сообщений
из множества T .
Результаты кодирования приведены в табл. 11.2.
Таблица 11.2
|
2 |
p( 2 ) |
J ( 2 ) log2 |
p( 2 ) |
Код |
1 |
u1u1 |
1/4 |
2 |
|
00 |
2 |
u1u2 |
1/6 |
2,58 |
|
01 |
3 |
u1u3 |
1/12 |
3,58 |
|
11 |
4 |
u2u1 |
1/6 |
2,58 |
|
10 |
5 |
u2u2 |
1/9 |
3,17 |
|
11 |
6 |
u2u3 |
1/18 |
4,17 |
|
11 |
7 |
u3u1 |
1/12 |
3,58 |
|
11 |
8 |
u3u2 |
1/18 |
4,17 |
|
11 |
9 |
u3u3 |
1/36 |
5,17 |
|
11 |
8.4. Расчет условных энтропий проводится по следующим формулам:
H ( A) p( 1 ) log2 p( 1 ) 2 ,
1 A
H ( A/ A1 ) p( 1 ) p( 2 / 1 ) log2 p( 2 / 1 ) 1,75 ,
1 A 2 A
H(A/ A2 ) p( 1 ) p( 2 / 1 ) p( 3 / 1 2 )log2 p( 3 / 1 2 )
1 A 2 A 3 A
p( 1 ) p( 2 / 1 ) p( 3 / 2 )log2 p( 3 / 2 ) 1,75,
1 A 2 A 3 A
...
H(A/ A ) lim H(A/ A ) 1,75.
8.5. Результаты кодирования приведены в табл. 11.3. Эффективность кодирования при этом составила
Э |
|
H (A / A ) |
|
1,75 |
|
0,98 . |
|
|
|
|
|
|
|
3,75 / 2 |
|
(n / ) log |
2 |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 11.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1a1 |
|
|
|
|
|
000 |
|
|
a1a3 |
|
|
11000 |
a2 a4 |
|
1/8 |
|
001 |
|
|
a1a4 |
|
|
11001 |
a3a3 |
|
|
010 |
|
|
a2 a2 |
|
|
11010 |
|
|
|
|
|
|
|
|
|
a4 a2 |
|
|
|
|
|
011 |
|
|
a2 a3 |
|
1/32 |
11011 |
a1a2 |
|
|
|
|
1000 |
|
|
a3a1 |
|
11100 |
|
|
|
|
|
|
a2 a1 |
|
1/16 |
1001 |
|
|
a3a2 |
|
|
11101 |
a3a4 |
|
1010 |
|
|
a4 a1 |
|
|
11110 |
|
|
|
|
|
|
a4 a3 |
|
|
|
|
1011 |
|
|
a4 a4 |
|
|
11111 |
8.6. В соответствии с основной теоремой кодирования
2 n 2,1 .
8.7. Метод универсального кодирования (УК – метод Бабкина) применяется в случае неизвестных статистических характеристик источника сообщений и состоит в следующем. Пусть в накоплен-
ном n - блоке имеется k единиц и (n-k) нулей. Пронумеруем последовательно нули и единицы, встречающиеся в n - блоке. Пусть
i1 , i 2 , . . . , i k |
– номера позиций единиц. |
|
|
|
|
|
|
Положим bk |
i |
1 |
1 |
i |
2 |
1 |
i |
k |
1 |
где |
|
– |
|
|
|
|
... |
|
, |
|
|
|
1 |
|
|
2 |
|
|
k |
|
|
|
|
|
|
|
|
|
биномиальный коэффициент, причем полагаем |
= 0 |
при . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае справедливы следующие утверждения:
|
|
|
|
n |
|
|
1. |
0 b k |
|
|
|
|
1 . |
|
k |
|
|
|
|
|
|
n - блоками и парами чисел k , bk - |
2. |
Соответствие между |
взаимно однозначно.
Тогда кодовое слово, соответствующее n - блоку, определяется |
как упорядоченная пара двоичных наборов |
k , bk |
. |
При этом |
длина кодового слова |
l |
|
log |
|
( n 1) |
|
|
log |
n |
|
, где |
n , k |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
]x[ – наименьшее большое целое.
Для порожденной источником последовательности имеем
|
|
|
|
|
i1 |
i 2 |
|
i 3 |
i 4 |
|
i 5 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
i1 |
|
2 , |
|
|
|
|
|
|
|
i 2 |
|
3 , |
|
|
|
|
|
|
|
i 3 |
|
5 , |
|
|
|
|
|
|
|
i 4 6 , |
|
n 8 , k |
5 , |
|
|
i 5 |
8 , |
|
l n , k |
|
4 |
6 . |
|
|
Построим для этого случая таблицу вычисления биномиальных коэффициентов (табл. 9.5).
Таблица 11.4
|
n |
n 1 |
n 1 |
n 1 |
n 1 |
n 1 |
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
i5 |
8 |
|
7 |
|
21 |
|
|
35 |
|
|
35 |
|
|
21 |
|
|
|
7 |
|
6 |
|
15 |
|
|
20 |
|
|
15 |
|
|
6 |
|
|
i 4 |
6 |
|
5 |
|
10 |
|
|
10 |
|
|
5 |
|
|
1 |
|
|
i 3 |
5 |
|
4 |
|
6 |
|
|
4 |
|
|
1 |
|
|
0 |
|
|
|
4 |
|
3 |
|
3 |
|
|
1 |
|
|
0 |
|
|
0 |
|
|
i 2 |
3 |
|
2 |
|
1 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
i 1 |
2 |
|
1 |
|
0 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
1 |
|
0 |
|
0 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
В таблице слагаемые, соответствующие искомым биномиальным коэффициентам, обведены,
bk 32, (k , bk ) (0101,100000) .
Декодирование производится в обратном порядке; так как k=5, ищем в 5-м столбце наибольшее число, меньшее или равное 32. Вычисляем разность 32-21=11. В 4-м столбце имеем наибольшее число, меньшее или равное 11, и т.д. Таким же образом декодирование производится при любом n.
8.8. Для решения задачи достаточно воспользоваться свойством стационарности дискретного марковского источника. Источник стационарен, так как все распределения вероятностей не зависят от
iи справедливо соотношение
p( i 1) p( i / i 1) p( i ) .
i 1 Ai 1
Более того, для стационарного состояния источника можно принять
p( i 1) p( i 1 1); p( i 0) p( i 1) 1;
Jlog2 p( i 1)
log2 0,4 1,322 .
9.1. Дискретный двоичный канал (ДК) без памяти задается матрицей условных (переходных) вероятностей
p(yi / xk ) |
|
|
|
|
|
1 p1 |
p1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
1 p2 |
|
|
|
В теории информации доказывается, что информационная пропускная способность дискретного стационарного канала может быть вычислена по формуле
C max H ( X ;Y ) ,
p ( xk )
p(xk ) 1,
X
где H ( X ; Y ) – взаимная энтропия. |
|
|
|
Вычислим |
пропускную способность ДК. |
Пусть |
p(x1 ) z , |
p(x2) 1 z . |
Тогда, |
используя формулу полной |
вероятности |
p( yi ) p(xk ) p( yi |
/ xk ) , представим вероятности |
выходного |
X |
|
|
|
|
|
пространства в виде |
|
|
|
|
p( y1 ) z(1 p1 ) (1 z) p2 z p2 , |
|
|
p( y2 ) zp1 (1 z)(1 p2 ) (1 p2 ) z, |
|
|
где 1 p1 p 2 . |
|
|
|
|
Подставляя эти значения в |
|
|
|
H ( X ;Y ) H (Y ) H (Y / X ) , |
|
|
|
H (Y ) p( yi ) log 2 p( yi ) , |
|
|
|
|
Y |
|
|
|
|
H (Y / X ) p( xk ) p( yi / xk ) log 2 |
p( yi |
/ xk ) , |
получаем |
X |
Y |
|
|
|
|
|
|
|
|
H (Y ) ( z p2 ) log 2 ( z p2 ) |
|
|
|
(1 p2 ) z log 2 (1 p2 ) z , |
|
|
|
H (Y / X ) z(1 p1 ) log 2 (1 p1 ) zp1 log 2 |
p1 |
(1 z) p2 log 2 p2 (1 z)(1 p2 ) log 2 (1 p2 ).
Находим |
экстремум, |
приравнивая |
нулю |
производную |
H ( X ;Y ) |
0 . После несложных преобразований получаем |
z |
|
|
1 |
p2 D |
|
|
|
|
|
z0 |
, |
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
где D 1 exp( B / ) ,
B p1 ln p1 (1 p1 ) ln(1 p1 ) p2 ln p2 (1 p2 ) ln(1 p2 ) .
Итак, информационная пропускная способность канала вычисляется по формуле C H ( X ;Y ) z z0 .
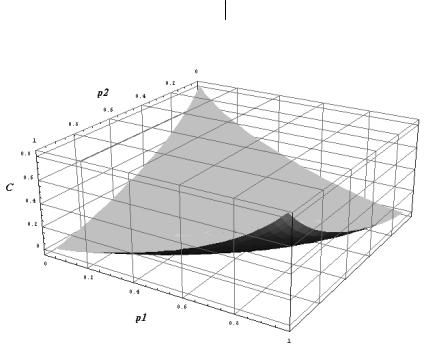
Поверхность C F[ p1 , p2 ] приведена на рис. 11.22.
Рис. 11.22. Поверхность Сдля двоичного канала
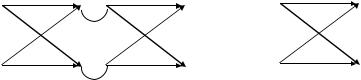
9.2. Эквивалентный канал (рис. 11.23) симметричен по входу и выходу. Следовательно,
C 1 (1 2 p 2 p2 )log2 (1 2 p 2 p2 ) (2 p 2 p2 )log2 (2 p 2 p2 ) .
Рис. 11.23. Граф-схема эквивалентного канала
9.3.C 0,919 бит.
9.4.Эквивалентный канал – ДСКС. Следовательно,
C (1 p)2 log 2 (1 p)2 |
p2 log 2 p2 |
|
(1 2 p |
2 p |
2 |
) log 2 |
(1 |
2 p 2 p2 ) |
. |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9.5. Эквивалентный канал – ДК. Следовательно, |
|
C 1 (1 p)2 log2 (1 p)2 |
(2 p p2 ) log2 (2 p p2 ) . |
9.6. C 2 p log |
|
p |
(1 p) log |
|
1 p . |
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
9.7. C 2 p log2 |
p (1 p) log2 |
(1 p) . |
|
Данное решение находится с учетом того обстоятельства, что
lim p log2 p 0 .
p 0
9.8. Решив экстремальную задачу с ограничением
C max H ( X ;Y ) H (Y ) H (Y / X ) ,
p(xk ) 1,
k 1
получим информационную пропускную способность заданного канала
C log 2 (1 21 p log 2 p (1 p) log 2 (1 p) ) .
289
10.1. На приемном конце принята комбинация
x7 x6 x5 x4 x3 x2 x1 . |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
Вычислив опознаватель
o1 x1 x3 x5 x7 1, o2 x2 x3 x6 x7 0,
o3 x4 x5 x6 x7 1,
исправляем 5-й разряд. Следовательно, был передан код 1001011. Образующая матрица группового кода Хэмминга (7,4) имеет
вид
|
|
|
|
|
7 |
6 |
5 |
3 |
|
4 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
: |
0 |
1 |
1 |
|
|
|
|
|
|
|
M n,k |
|
IkT : Bn k ,k |
|
|
0 0 1 |
0 |
: 1 |
0 |
1 |
, |
|
|
|
|
|
|
|
0 |
1 |
0 0 |
: |
1 |
1 |
0 |
|
|
|
|
|
|
1 |
0 |
0 |
0 |
: |
1 |
1 |
1 |
|
который позволяет достаточно просто убедиться в правильности принятого решения.
10.2. На приемном конце принята комбинация |
7 |
6 |
5 |
4 |
3 |
2 |
1 . |
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
Производим деление многочленов |
|
|
|
|
|
|
|
|
|
x6 x3 x 1 |
|
|
|
x3 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x6 x4 x3 |
|
|
|
x3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
x 1 |
|
|
|
|
|
|
|
|
|
x4 |
x2 |
x |
|
|
|
|
|
|
|
|
x2 1
По таблице ошибок (табл. 10.11) находим, что искажение произошло в разряде 7. Исправляем этот разряд. Следовательно, был передан код 0001011.
Образующая матрица циклического кода Хэмминга (7,4) имеет вид