Раздел 6.Конечные автоматы

Практическая работа №14

ПОСТРОЕНИЕ МИНИМАЛЬНЫХ АВТОМАТОВ

1. Общие сведения

Конечный автомат состоит из конечного управления и входной ленты, разбитой на ячейки. В каждой ячейке записан один символ из входного алфавита Σ, и все они образуют конечную входную цепочку. Конечное управле­ние первоначально находится в состоянии q₀ и сканирует крайнюю левую ячей­ку ленты. По мере чтения входной цепочки слева направо автомат переходит в другие состояния из множества Q. Если, прочитав входную цепочку, автомат оказывается в некотором конечном состоянии из множества F, то говорят, что он принял ее. Множество цепочек, принимаемых конечным автоматом, называется языком, распознаваемым данным конечным автоматом.

Определение. Конечным автоматом называется формальная система M = (Q, Σ, δ, q₀, F), где Q - конечное непустое множество состояний; Σ - ко­нечный входной алфавит; δ - отображение типа QxΣ → Q; q₀ Q - началь­ное состояние; FQ - множество конечных состояний.

Запись δ(q, a) =p, где q p, Q и aΣ, означает, что конечный автомат M в состоянии q, сканируя входной символ a, продвигает свою входную головку на одну ячейку вправо и переходит в состояние p .

Автомат «вообще»- управляющая система, являющаяся конечным автоматом или некоторой его модификацией, полученной путем изменения его компонент или функционирования. Основное понятие - конечный автомат - возникло в середине 20 века в связи с попытками описать на математическом языке функционирование нервных систем, универсальных вычислительных машин и других реальных автоматов. Характерной особенностью такого описания является дискретность соответствующих математических моделей и конечность областей значений их параметров, что приводит к понятию конечного автомата.

Наряду с понятием конечного автомата рассматриваются различные его обобщения и модификации, отражающие те или иные особенности реальных устройств. Для конечного автомата (A, S, B, , ) существующие модификации можно разбить на следующие три основные группы.

• К первой группе относятся автоматы, у которых некоторые из алфавитов A (входной), S (состояний) или B (выходной) бесконечны, в связи с чем такие автоматы называются бесконечными.

• Ко второй группе относятся автоматы, у которых вместо выходной и переходной функций  и  допускаются произвольные отношения или случайные функции. Таковы частичные, недетерминированные, вероятностные и другие автоматы.

• К третьей группе относятся автоматы со специфическими множествами входных объектов. Таковы, например, автоматы с переменной структурой.

Существуют автоматы, принадлежащие одновременно разным группам. Наряду с этим большую роль играют специальные подклассы конечных автоматов, например, автоматы без памяти. Кроме того, использование понятий и методов из других разделов математики также приводит к появлению специфических классов автоматов и связанных с ними задач. Например, при применении алгебраических средств возникают понятия автоматов над термами, линейного, группового, свободного и других; вопросы теории кодирования порождают понятия самонастраивающихся, обратимых автоматов и другие.

Теория автоматов - это раздел теории управляющих систем, изучающий математические модели преобразователей дискретной информации, называемые автоматами. С определенной точки зрения такими преобразователями являются как реальные устройства (вычислительные машины, автоматы, живые организмы и т.д.), так и абстрактные системы (например, формальная система, аксиоматические теории и т.д.). Наиболее тесно теория автоматов связана с теорией алгоритмов.

Большинство задач теории автоматов - общие для основных видов управляющих систем. К ним относятся задачи анализа и синтеза автоматов, задачи полноты, минимизации, эквивалентных преобразований автоматов и другие.

• Задача анализа состоит в том, чтобы по заданному автомату описать его поведение или по неполным данным об автомате и его функционированию установить те или иные его свойства.

• Задача синтеза автоматов состоит в построении автомата с наперед заданным поведением или функционированием. Задача полноты состоит в выяснении, обладает ли множество M'   M автоматов свойством полноты, т.е. совпадает ли с M множество всех автоматов, которые получаются путем конечного числа применений некоторых операций к автоматам из заданного подмножества автоматов M'  .

• Задача эквивалентных преобразований в общем виде состоит в том, чтобы найти систему правил преобразований (так называемую полную систему правил) автоматов, которые удовлетворяют определенным условиям и позволяют преобразовать произвольный автомат в любой эквивалентный ему автомат (два автомата эквивалентны, если они имеют одинаковое поведение автомата. Поведение автомата - математическое понятие, описывающее взаимодействие автомата с внешней средой. Примером внешней среды конечного автомата является множество входных слов, а поведением - словарная функция, реализуемая автоматом, или событие, представимое автоматом.)

Теория автоматов находит применение как и в других областях математики, так и в решении практических задач. Например, средствами теории автоматов доказывается разрешимость некоторых формальных исчислений. Применение методов и понятий теории автоматов к изучению формальных и естественных языков привело к возникновению математической лингвистики (математическая лингвистика - математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков.) Понятие автомата может служить модельным объектом в самых разнообразных задачах, благодаря чему возможно применение теории автоматов в различных научных и прикладных исследованиях.

Способы задания автоматов.

• Во-первых, автомат может быть задан в виде непосредственного описания функций:

fq1={q2 (x1/y1); q3 (x2/y2); q4 (x3/y1)}

fq2={q1(x1/y1); q2 (x1/y2); q3 (x3/y2)}

fq3={q3 (x1/y2); q1 (x2/y1); q2 (x3/y1)}

fq4={q4(x1/y1); q2 (x2/y2); q1 (x3/y2)},

где X={x1, x2, x3} –входной алфавит

Z={q1,q2,q3,q4} – множество состояний автомата

Y={y1,y2} – выходной алфавит

• Во-вторых, уравнения могут быть представлены в табличной форме.

Таблица перехода

X(t) Z(t)	Z(t+1)
	a1	a2	a3
q1	q2	q3	q4
q2	q1	q2	q3
q3	q3	q1	q2
q4	q4	q2	q1

Z(t+1)=f(x(t);z(t))

f(ai, qi)=qj

Таблица выхода

X(t) Z(t)	y(t)
	a1	a2	a3
q1	y1	y2	y1
q2	y1	y2	y2
q3	y2	y1	y1
q4	y1	y2	y2

y(t)=g(x(t); z(t))

ai=xi/yi

• В-третьих, таблицы переходов и выходов можно объединить в одну. Содержимое каждой клетки представляет собой дробь: над косой чертой вписывается соответствующее значение из таблицы переходов, под косой чертой – значение из таблицы выходов. Полученная таким образом таблица называется общей таблицей переходов и выходов конечного автомата.

• Граф автомата (графоид) – это сигнальный граф, вершины которого обозначают состояния автомата, на дугах отражены условия перехода из состояния в состояние и значения выходных сигналов в виде дроби: над косой чертой – x(j), под ней – y(j).

• Конечный автомат можно также описать с помощью матрицы переходов. Это аналог графа в табличной форме. Она представляет собой квадратную матрицу размерности число состояний  число состояний, в которой отражены условия перехода из состояния в состояние аналогично изображённым на графе.

Общее определение конечного автомата:

 

                                              M = (X, Y, S, δ, λ),                                 

Пример. Рассмотрим диаграмму состояний конечного автомата. Пусть задан конечный автомат M = (Q, Σ, δ, q₀, F), где Q = {q₀, q₁, q₂, q ₃}, Σ = {0,1}, F = {q₀}, δ(q₀, 0) = q₂, δ(q₀, 1) = q₁ , δ(q₁, 0) = q₃ , δ(q₁, 1) = q₀ , δ(q₂, 0) = q₀ , δ(q₂, 1) = q₃ , δ(q₃, 0) = q₁ , δ(q₃, 0) = q₂

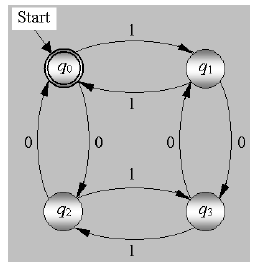
Рисунок 1

Диаграмма состояний конечного автомата состоит из узлов, представляющих состояния, и из ориентированных дуг, определяющих возможные переходы, которые зависят от входных символов. Так, если δ(q, a) = p, то из узла, представляющего состояние q, в узел, представляющий состояние p, проводится дуга, помеченная входным символом a. На рис.1 дана диаграмма состояний конечного автомата M. Двойным кружком выделено единственное в данном примере конечное состояние, которое является одновременно и начальным.

По способу формирования функций выходов выделяют автоматы Мили и Мура. В автомате Мили функция выходов λ определяет значение выходного символа по классической схеме абстрактного автомата. Математическая модель автомата Мили и схема рекуррентных соотношений не отличаются от математической модели и схемы рекуррентных соотношений абстрактного автомата. Таким образом, можно дать следующее определение:

Конечным детерминированным автоматом типа Мили называется совокупность пяти объектов

,

где S, X и Y — конечные непустые множества, а δ и λ — отображения вида:

и со связью элементов множеств S, X и Y в абстрактном времени T = {0, 1, 2, …} уравнениями:

(Отображения δ и λ получили названия, соответственно функции переходов и функции выходов автомата A).

Особенностью автомата Мили является то, что функция выходов является двух аргументной и символ в выходном канале y(t) обнаруживается только при наличии символа во входном канале x(t). Функциональная схема не отличается от схемы абстрактного автомата.

Зависимость выходного сигнала только от состояния представлена в автоматах типа Мура. В автомате Мура функция выходов определяет значение выходного символа только по одному аргументу — состоянию автомата. Эту функцию называют также функцией меток, так как она каждому состоянию автомата ставит метку на выходе.

Конечным детерминированным автоматом типа Мура называется совокупность пяти объектов:

где S, X, Y и δ — соответствуют определению автомата типа Мили, а μ является отображением вида: μ : S → Y, с зависимостью состояний и выходных сигналов во времени уравнением:

.

Особенностью автомата Мура является то, что символ y(t) в выходном канале существует все время пока автомат находится в состоянии s(t).