дискретка_все_практики / дискретка / Razdel_5_Praktika_13

Раздел 5. Элементы теории графов

ПРАКТИЧЕСКАЯ РАБОТА №13

МАКСИМАЛЬНЫЙ ПОТОК В СЕТИ

1. ОБЩИЕ СВЕДЕНИЯ

Ориентированный граф (кратко орграф) - граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами.

Транспортной сетью называется конечный связный орграф G(V, E) без петель, каждой дуге которого поставлено в соответствие некоторое неотрицательное число c(), называемое пропускной способностью дуги, и существует:

1)   ровно одна вершина, в которую не заходит ни одна дуга, называемая источником или началом сети;

2)   ровно одна вершина, из которой не выходит ни одной дуги; эта вершина называется стоком или концом сети.

Потоком сети называется неотрицательная функция f(1) такая, что f(e) меньше или равно c(e). (Поток не может превышать пропускную способность дуги.)

Дуга называется насыщенной потоком f, если f(e)=c(e).

Поток называется полным, если содержит насыщенную дугу f(e)=c(e).)

Разрезом L  сети G(V,E) называется множество насыщенных дуг, отделяющих источник s от стока t.

Сформулируем некоторые леммы.

Лемма 1. Величина потока через любой разрез одна и та же.

Лемма 2. Для любого потока f и любого разреза (X, )

val(f₀)=c(X, ).

Лемма 3. Если для некоторого потока f₀ и некоторого разреза (X ,X ₀)

val(f₀) = c(X₀, ), то величина потока f₀ - максимально возможная, а пропускная способность разреза (X₀, )- наименьшая из пропускных способ­ностей разрезов сети.

Изучение максимальных потоков через сеть тесно связано с понятием разреза, т.е. такого множества дуг орграфа , которое обладает тем свойством, что любая простая орцепь из в проходит через дугу, принадлежащую . Другими словами, разрезом в сети является не что иное, как — разделяющее множество соответствующего орграфа . Пропускной способностью разреза называется сумма пропускных способностей принадлежащих ему дуг. Мы будем рассматривать главным образом такие разрезы, которые обладают наименьшей возможной пропускной способностью, — так называемые минимальные разрезы.

Величина любого потока не превышает пропускной способности любого разреза, и, следовательно, величина любого максимального потока не превышает пропускной способности любого минимального разреза. Однако сразу не ясно, что два последних числа всегда равны между собой; этот замечательный результат называется теоремой о максимальном потоке и минимальном разрезе. Впервые она была доказана Фордом и Фалкерсоном в 1955,г.

Теорема (о максимальном потоке и минимальном разрезе). Во всякой сети величина любого максимального потока равна пропускной способности любого минимального разреза.

Отметим еще раз, что сетью называют взвешенный орграф с двумя выделенными верши­нами: истоком и стоком. Исток имеет нулевую полустепень захода, а сток нулевую степень исхода.

Вес дуг означает, как правило, пропускную способность дуги. Задача о наибольшем потоке в сети не единственная, но вероятно, основная задача для потоков в сети. Очевидно практи­ческое применение решения этой задачи для решения транспортных проблем (пробки на дорогах это и есть насыщение сети или отдельной ее дуги), проблем транспортировки нефтепродуктов или электричества.

Задача. Задана пропускная способность дуг транспортной сети (рис. 1) с началом в вершине 1 и концом в вершине 8. Используя алгоритм Форда-Фалкерсона, найти максимальный поток по сети.

Рисунок 1

Решение

Алгоритм из двух частей — насыщение потока и его перераспреде­ление. В первой части задача ставится локально. Дуги рассматриваются отдельно (возможно хаотично) и каждой дуге приписывается возможно больший поток, согласованный только с условием сохранения в узлах (вершинах). Во второй части перераспределения потока выполняется из условия достижения общего по сети максимума потока.

Рассмотрим алгоритм Форда — Фалкерсона:

Дан граф G(V,E) с пропускной способностью c(u,v) и потоком f(u,v) = 0 для ребер из u в v. Необходимо найти максимальный поток из источника s в сток t. На каждом шаге алгоритма действуют те же условия, что и для всех потоков:

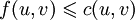• . Поток из u в v не превосходит пропускной способности.

• .

• для всех узлов u, кроме s и t.

Поток не изменяется при прохождении через узел.

Остаточная сеть G_f(V,E_f) — сеть с пропускной способностью c_f(u,v) = c(u,v) − f(u,v) и без потока.

Вход Граф с пропускной способностью , источник и сток Выход Максимальный поток из в

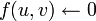1. для всех ребер

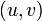
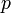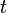2. Пока есть путь из в в , такой что для всех ребер :

1. Найти

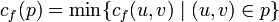
2. Для каждого ребра

1. 

2. 

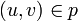
1. Насыщение потока (нахождение наибольшего потока)

Поток называется насыщенным, если любой путь из истока (1) в сток (8) содержит насыщенную дугу.

Рассмотрим путь 1-2-4-6-8. Пропустим через этот путь поток равный 4. При этом дуга 2-4 и 4-6 будут насыщенными. Аналогично, путь 1-3-5-7-8 насытим потоком 4. Распределение потока отметим на графе. В числителе ставим пропускную способность, в знаменателе — поток. Числитель всегда больше знаменателя, знаменатель может быть и нулем.

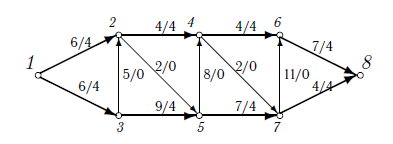
Рисунок 2

Заметим, что из 1 в 8 есть еще ненасыщенный путь 1-3-2-5-4-7-6-8, в котором можно увеличить поток на 2. При этом насытятся дуги 1-3, 2-5, 4-7.

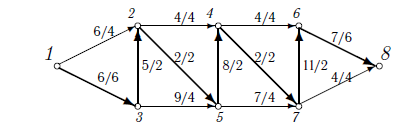
Рисунок 3

Из 1 в 8 больше нет ненасыщенных путей. По дуге 1-3 двигаться нельзя (она уже насыщена), а движение по дуге 1-2 заканчивается в вершине 2, так как обе выходящие из нее дуги насыщены.

2. Перераспределение потока (построение наибольшего потока).

Найдем последовательность вер­шин из 1 в 8, такую, что дуги, соединяющие соседние вершины, направленные из 1 в 8 ненасыщены, а дуги, направленные в обратном направлении не пусты. Имеем единственную последовательность 1-2-3-5-7-6-8. Перераспределяем поток. Поток в дугах прямого направления увеличиваем на 1, а поток в дугах обратного направления уменьшаем на 1. Процесс продолжаем до тех пор, пока одна из прямых дуг будет насыщена или какая-нибудь обратная дуга будет пуста.

Рисунок 4

Поток в насыщенной сети можно посчитать по потоку выходящему из истока 1, или по входящему в 8. Очевидно, эти числа должны быть равны. Кроме этого для проверки решения следует проверить условие сохранения потока по узлам. В каждый узел суммарный входящий поток должен быть равен выходящему. В рассматриваемом примере поток равен 11. Распределение потока по дугам при одном и том же суммарном минимальном потоке по сети неединственно.

Существуют и другие методы нахождения максимального потока. Путь может быть найден, например, поиском в ширину (алгоритм Эдмондса-Карпа) или поиском в глубину в G_f (V,E_f).

2. ЦЕЛЬ И ПОРЯДОК РАБОТЫ

Цель работы - получить первичные знания о теории графов .Изучить алгоритм нахождения максимального потока

Порядок выполнения работы:

• изучить описание работы;

• согласно своему варианту задания, решить заданные примеры без применения ЭВМ

• разработать алгоритмы решения отдельных задач и оформить в виде процедур

• разработать и отладить программу в соответствии с заданием;

• проверить с помощью программы результат ручного просчета .

• оформить отчет.

3. ЗАДАНИЯ

3.1 Задания для ручного просчета:

Дана сеть (G,), s – источник, t – сток сети, :EN (Цифрами указаны пропускные способности дуг ). Построить максимальный поток для сети, соответствующей вашему варианту (пример решения задания смотри в Общих сведениях)

1) 2

1 2

3

5

s 4 t

7

8

2) 2

3 4

4 7

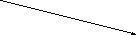
s 5 t

1 2

3)

3 2

3 4

s 7

3

4

4 t

4)

4

6

3

4

5 t

s 4 5

5)

2 6

6

7 t

s 5 5

2 9

3

6)

3 6

2 5

1 t

s 6 4

3

4

7)

3 7

1

3

6

s t

5 2 5

3.2 Задания для вычисления с помощью программы

Дан граф:

Согласно своему варианту разработать программу для поиска максимального потока, используя известную вам среду программирования.

3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

• Алгоритм нахождения максимального потока в сети поиском в ширину (алгоритм Эдмондса-Карпа)

FindPath(source, target) - поиск пути по которому возможно пустить поток алгоритмом обхода графа в ширину, функция ищет путь из истока в сток по которому еще можно пустить поток, считая вместимость ребера (i,j) равной c[i][j] - f[i][j]

// f - массив содержащий текушее значение потока

// f[i,j] - поток текущий от вершины i к j

// kv – количество вершин графа

//функция поиска максимального потока

public int MaxFlow(int source, int target) // source - исток, target - сток

{

// инициализируем переменные:

for (int j = 0; j < kv; j++)// по графу ничего не течет

for (int r = 0; r < kv; r++)

f[j, r] = 0;

int MaxFl = 0; // начальное значение потока

int AddFlow;

do

{

// каждую итерацию ищем какой-либо простой путь из истока в сток

// и какой еще поток моожет быть пущен по этому пути

AddFlow = FindPath(source, target);

MaxFl += AddFlow;

} while (AddFlow > 0); // повторяем цикл пока поток увеличивается

return MaxFl;

}

• Реализуем алгоритм поиска максимального потока в сети на языке Pascal

#include <stdio.h> #include <math.h> int C[202][202],F[202][202],P[202][2],oo=(1<<25),; bool fl; int MIN(int A,int B) { if(A<B) return A; return B; } void Stream(int N,int i) { if(P[i][0]>0) F[P[i][0]-1][i]+=P[N-1][1]; else F[i][abs(P[i][0])-1]-=P[N-1][1]; if(abs(P[i][0])!=N-1) Stream(N,abs(P[i][0])-1); } void Mark(int N) { bool *Nnew=new bool[N]; int i,seek=N-2; for(i=0;i<N;i++) Nnew[i]=1; P[seek][0]=seek+1; P[seek][1]=oo; while(!P[N-1][0] && fl) { for(i=0;i<N;i++) if(!P[i][0] && (C[seek][i] || C[i][seek])) { if(F[seek][i]<C[seek][i]) { P[i][0]=seek+1; P[i][1]=MIN(P[seek][1],C[seek][i]-F[seek][i]); } else if(F[i][seek]>0) { P[i][0]=-seek-1; P[i][1]=MIN(P[seek][1],F[i][seek]); } } Nnew[seek]=0; seek=0; while(seek<N && (!Nnew[seek] || !P[seek][0])) seek++; if(seek>=N) fl=0; } } bool FordF(int N) { while(1) { for(i=0;i<N;i++) P[i][0]=0; Mark(N); if(!fl) break; Stream(N,N-1); } }

• На языке C алгоритм можно реализовать следующим образом:

Идея данного алгоритма состоит в нахождении сквозных путей с положительными потоками от источника к стоку.

#include <iostream.h>

#include <stdlib.h> //Для функции abs().

#define TRUE 1

#define FALSE 0

#define MaxNodes 5 //Количество вершин.

#define MaxInt 1000 //Машинный эквивалент бесконечности.

//Описание типа узла.

struct Uzel

{

int Element; //Заданный номер вершины.

int Propusk; //Пропускная способность.

int Metka; //Помечена вершина или нет.

};

class Spisok

{

private:

int C[MaxNodes][MaxNodes]; //Матрица начальных пропускных способностей.

int c[MaxNodes][MaxNodes]; //Матрица конечных пропускных способностей.

int Put[MaxNodes][MaxNodes]; //Матрица сквозных путей.

int Potok [MaxNodes]; //Потоки.

int Est (Uzel*,int,int);

int Tpk (int*,int,int);

public:

void Vvod_Ves();

int Reshenie ();

void Vyvod(int);

};

void main()

{

Spisok A;

A.Vvod_Ves();

A.Vyvod(A.Reshenie());

}

void Spisok::Vvod_Ves()

//Ввод матрицы пропускных способностей.

{

cout << "Вводите пропускные способности ребер:\n";

for (int i=0;i<MaxNodes;i++)

for (int j=0;j<MaxNodes;j++)

{

cout << "Введите C[" << (i+1) << "," << (j+1) << "]: ";

cin >> C[i][j];

c[i][j] = C[i][j];

}

}

void Spisok::Vyvod(int n)

//Вывод результатов.

{

//Вычисление максимального объема потока.

for (int i=0,sum=0;i<=n;sum+=Potok[i++]);

cout << "\nМаксимальный объем потока в сети: " << sum;

cout << "\nЗначения потоков по различным ребрам:\n";

for (i=0;i<MaxNodes;i++)

for (int j=i;j<MaxNodes;j++)

if (C[i][j])

{

cout << "Ребро (" << (i+1) << "," << (j+1) <<"): ";

cout << "(" << C[i][j] << "," << C[j][i] << ")-(";

cout << c[i][j] << "," << c[j][i] << ")=(";

cout << (C[i][j]-c[i][j]) << "," << (C[j][i]-c[j][i]) << ") ";

cout << "Поток: " << abs(C[i][j]-c[i][j]) << " ";

if (C[i][j]-c[i][j]!=0)

{

cout << "Направление: ";

if (C[i][j]-c[i][j]>0)

cout << (i+1) << "->" << (j+1);

else

cout << (j+1) << "->" << (i+1);

}

cout << endl;

}

}

int Spisok::Reshenie()

{

Uzel SS[MaxNodes]; //Множество узлов, в которые можно перейти.

Uzel S[MaxNodes]; //Путь.

int i,j=0,k,el,mx,mn;

int m; //Текущее количество вершин в пути.

int nomer=-1; //Текущее количество сквозных потоков.

int Tupik[MaxNodes]; //Перечень "тупиковых" вершин.

int N_Tupik; //Количество элементов в массиве.

while (j!=-1)

{

i=m=0;

S[i].Element=0;

S[i].Propusk=MaxInt;

S[i].Metka=TRUE;

el=0;

N_Tupik=-1;

while (el!=MaxNodes-1)

{

j=-1;

for (k=0;k<MaxNodes;k++)

if (c[i][k]!=0) //Если есть ненулевой поток...

if (i>0) //и в путь уже включены вершины...

{

if (!Est(&S[0],m,k) && !Tpk(&Tupik[0],N_Tupik,k))

//то включаем текущую вершину,

//если ее нет в пути и если она не "тупиковая".

{

SS[++j].Element=k;

SS[j].Propusk=c[i][k];

SS[j].Metka=FALSE;

}

}

else

if (!Tpk(&Tupik[0],N_Tupik,k)) //Не вернулись ли назад?

//Поток не нулевой, и это первая вершина.

{ //Включаем эту вершину в путь.

SS[++j].Element=k;

SS[j].Propusk=c[i][k];

SS[j].Metka=FALSE;

}

if (j!=-1) //Есть продолжение.

{

mx=SS[0].Propusk;

el=0;

for (k=1;k<=j;k++)

if (SS[k].Propusk>mx)

{ el=k; mx=SS[k].Propusk; }

S[++m].Element=SS[el].Element;

S[m].Propusk=mx;

S[m].Metka=TRUE;

if (SS[el].Element==MaxNodes-1) //Найден сквозной путь.

{

nomer++;

//Запоминаем сквозной путь.

for (k=0;k<=m;k++)

Put[nomer][k]=S[k].Element;

//Ищем минимальный поток.

mn=S[0].Propusk;

el=0;

for (k=1;k<=m;k++)

if (S[k].Propusk<mn)

{ el=k; mn=S[k].Propusk; }

Potok[nomer]=mn; //Запоминаем его.

//Вычисляем остаточные пропускные способности.

for (k=0;k<m;k++)

{

c[S[k].Element][S[k+1].Element] -= Potok[nomer];

c[S[k+1].Element][S[k].Element] += Potok[nomer];

}

el=MaxNodes-1; //Переход к следующей итерации.

j=0;

}

else i=S[m].Element;

}

else //Продолжения нет. Это возможно тогда, когда:

{

if (i==0) //а) все пропускные способности нулевые.

// В этом случае - выход

el=MaxNodes-1;

else //б) мы попали в тупик. Запомним тупиковую вершину

// в массиве и отступим назад на одну вершину.

{

Tupik[++N_Tupik]=S[m].Element;

m--;

i=S[m].Element;

}

}

}

}

return nomer; //Возвращает количество сквозных потоков.

}

int Spisok::Est(Uzel S[], int m, int k)

//Функция проверяет, есть ли вершина k в пути S.

//m - текущее количество элементов в пути.

//Возвращает 1, если вершина есть, и 0 - в противном случае.

{

for (int l=0;l<=m;l++)

if (S[l].Element==k) return 1;

return 0;

}

int Spisok::Tpk(int Tupik[],int N_Tupik, int k)

//Функция проверяет, есть ли вершина k в массиве "тупиковых" вершин.

//N_Tupik - текущее количество вершин в массиве.

//Возвращает 1, если вершина есть, и 0 - в противном случае.

{

if (N_Tupik==-1) return 0;

for (int l=0;l<=N_Tupik;l++)

if (Tupik[l]==k) return 1;

return 0;

}

• Поиск возможного пути из х0 в z :

k:=0;

j:=1;

usl:=0;

repeat

if graf[i,1]=j then

begin

if graf[i,5]=0 then

begin

inc(k);

mas[k]:=i;

j:=graf[i,2];

l:=i;

i:=1;

end

else

begin

inc(i);

end;

end else inc(i);

if i>count-1 then

if graf[l,2]<>n then

begin

j:=graf[l,1];

graf[l,5]:=1;

mas[k]:=0;

i:=1;

dec(k);

if k=0 then j:=1;

end

until (graf[l,2]=n)or(k<0);

где graf[i,j] ¾ список инцидентности графа.

Mas[i] ¾ массив полученного пути (указаны строки списка инцидентности которые входят в найденный путь из х0 в z) .

Переменная к показывает количество дуг входящих в полученный путь.

Проверка на насыщенность :

for i:=1 to count-1 do

if graf[i,3]=graf[i,4] then

graf[i,5]:=1 else graf[i,5]:=0;

end;

где graf[i,5]¾ поле списка определяющее насыщенность дуги(0- ненасыщенная , 1- насыщенная ).

Насыщение найденного пути:

usl:=0; {переменная условия выхода}

if k>=0 then

repeat

for i:=1 to k do

begin

l:=mas[i];

graf[l,4]:=graf[l,4]+1;

end;

for i:=1 to k do

begin

l:=mas[i];

if graf[l,4]=graf[l,3] then usl:=1;

end;

until usl=1;

5. СОДЕРЖАНИЕ ОТЧЕТА

• наименование работы, постановку задачи;

• выбранный вариант задания;

• результаты решения задач без применения ЭВМ;

• программу решения задачи (представляется в электронном виде);

• результаты работы программы и их анализ.

6. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется ориентированным графом?

2. Дайте определение транспортной сети.

3. Может ли поток превышать пропускную способность дуги?

4. Какая дуга называется насыщенной?

5. Дать определение разреза.

6. Сформулируйте три леммы.

7. Кем была впервые предложена теорема о максимальном потоке и минимальном разрезе? Сформулируйте ее.

8. Каково практическое применение задачи о максимальном потоке?

9. Раскройте этапы алгоритма Форда—Фалкерсона.

10. На примере рис. 5 рассмотреть оба этапа алгоритма Форда— Фалкерсона.

Рисунок 5

11. Какие существуют еще методы нахождения максимального потока?

7. ОСНОВНАЯ ЛИТЕРАТУРА

1. А. И. Белоусов Дискретная математика: Учеб. пособие для втузов/Белоусов А. И., Ткачев С. Б., Под ред. Зарубина В. С., Ирищенко А. П. – 3-е изд., стер. – М.: Изд-во МГТУ им. Баумана, 2004. – 743 с.

2. Горбатов В. А. Дискретная математика: Учеб. для втузов В. А. Горбатов. – М.АСТ; Астель, 2003 – 447с (Высшая школа)

3. О. П. Кузнецов, Г. М. Адельсон-Вельский «Дискретная математика для инженера». - М.: Энергоатомиздат, 1988 – 479, [1] с.: кл., 22 см.

4. Оре, Ойстин Теория графов/ Пер. с англ. И. Н. Врублевской. Под редакцией Н. Н. Воробьева –2-е изд. Стереотипное. М.: Наука, 1980.-336с

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Басакер Р., Саати Т. Конечные графы и сети. М.: Наука, 1974. 368c.

2. Зыков А. А. Основы теории графов. — М.: «Вузовская книга», 2004. — С. 664. — ISBN 5-9502-0057-8(М.: Наука, 1987. 383c.)

3. Кормен Т. Х. и др. Часть VI. Алгоритмы для работы с графами // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд.. — М.: Вильямс, 2006. — С. 1296. — ISBN 0-07-013151-1