дискретка_все_практики / дискретка / Razdel_5_Praktika_12

Раздел 5. Элементы теории графов

ПРАКТИЧЕСКАЯ РАБОТА №12

ОПРЕДЕЛЕНИЕ ИЗОМОРФНОСТИ ГРАФОВ

1. ОБЩИЕ СВЕДЕНИЯ

Отображение графов - это отображение множеств вершин, которое сохраняет отношение смежности и, таким образом, индуцирует вполне определенное отображение на множестве ребер.

Графы G1=(V1,E1) и G2=(V2,E2) называются изоморфными (обозначение G1~G2), если между графами существует взаимнооднозначное отображение j: G1~G2 (V1~V2, E1~E2), которое сохраняет соответствие между ребрами (дугами) графов, т.е. для любого ребра (дуги) e=(v,u) верно:

e'=j(v,u)=(j(v),j(u)) (e~E1, e'~E2) (1)

Отображение j называется изоморфным отображением.

Дадим другое определение изоморфности: два графа G1 и G2 называются изоморфными, если между их вершинами установлено взаимнооднозначное соответствие, такое, что любые две вершины графа G1 соединены так же, как и соответствующие вершины графа G2

Рассмотрим графы 1 и 2

Рисунок 1 Изоморфные графы

На рисунке 1 видно, что между графами существует взаимнооднозначное соответствие, то есть, например, ребро (2,6) первого графа подобно ребру (2,6) второго графа. Это можно наблюдать для всех вершин и ребер.

    Иными словами, изоморфные графы различаются только обозначением вершин.

Условимся называть (0,1)-матрицу булевой, если с её элементами мы намерены обращаться по правилам булевой алгебры.

Изоморфизм графов можно определить в матричных терминах. Предварительно введём понятие перестановочного подобия матриц. Оно формулируется одинаково для булевых матриц и матриц над полем.

Квадратная (0,1)-матрица P называется перестановочной, если она имеет в каждой строке и каждом столбце ровно одну единицу. Легко проверить, что тогда

Матрицы A и B называются перестановочно подобными, если для некоторой перестановочной матрицы P. Содержательный смысл этого определения заключается в том, что A получается из B одинаковыми перестановками строк и столбцов.

Пусть графы с n вершинами, заданные матрицами смежности A и B, изоморфны, то есть существует такая биекция (перестановка) σ на множестве {1,2, ... , n}, что для любых ij

(2)

Сопоставим перестановке перестановочную матрицу P = (p) порядка n, где

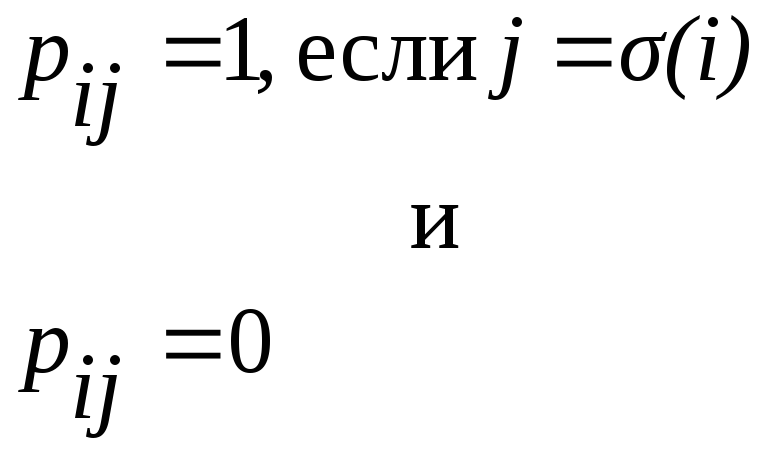(3)

Прямыми вычислениями проверяется, что

(4)

Итак, если графы изоморфны, то их матрицы смежности перестановочно подобны. Наоборот, если матрицы смежности перестановочно подобны, то графы изоморфны, причем изоморфизм σ определяется по матрице подобия P из равенств (3).

Вывод: графы изоморфны тогда и только тогда, когда их матрицы смежности перестановочно подобны.

В соответствии с определением изоморфизма графов у нас появляются варианты для организации проверки изоморфизма графов: либо мы для каждой пары графов ищем свое взаимнооднозначное соответствие, сохраняющее смежность; либо мы каждому графу взаимнооднозначно сопоставляем элемент некоторого одного и того же множества, сохраняющий информацию о смежности вершин графа, а затем ищем взаимнооднозначное соответствие между элементами этого множества. Понятно, что в последнем случае нас также интересует взаимнооднозначное соответствие, которое сохраняло бы информацию о смежности. В силу того, что взаимнооднозначное соответствие, сохраняющее смежность, рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности, эти два варианта организации проверки изоморфизма графов равнозначны относительно результата.

В качестве упоминаемого выше множества, элементам которого взаимнооднозначно сопоставляются графы, можно взять множество матриц смежности, поскольку каждая матрица смежности несет в себе информацию о смежности вершин графа. Тогда в качестве соответствующего взаимнооднозначного соответствия между парами матриц смежности будет отношение перестановочного подобия.

Для последующего рассмотрения алгоритма определения изоморфности двух графов дадим определение связных вершин и подграфа.

Вершины в графе связаны, если существует соединяющая их (простая) цепь, где цепь в графе — маршрут, все рёбра которого различны. Если все вершины (а тем самым и рёбра) различны, то такая цепь называется простой (элементарной).

Граф называется связным, если любые две его вер­шины связаны. Если граф не связен, то он представляет собой объ­единение нескольких связных подграфов.

Граф называется подграфом графа (V,E), если . Например, цепь в графе можно рассматривать как подграф. Говорят, что подграф порождён подмножеством вершин если состоит из рёбер, соединяющих вершины из . Говорят, что подграф порождён подмножеством рёбер если состоит из концов рёбер из .

Легко убедиться, что бинарное отношение связанности на мно­жестве вершин графа рефлексивно, симметрично и транзитивно, то есть, связанность вершин является отношением эквивалентности.

Замечание. Многие практические задачи приводят к необходимости распознавания изоморфизма и изоморфного вложения сложных структур, заданных в виде графов. С содержательной точки зрения изоморфизм графов структур означает тождественность функционирования самих структур, что допускает в некоторых случаях замену одной структуры другой, ей изоморфной. Однако для того чтобы выяснить, изоморфны ли два графа имеющие  вершин, в общем случае требуется выполнить  попарных сравнений, а для распознавания изоморфного вложения графа , имеющего  вершин, в граф , у которого  вершин, необходимо провести  сравнений. Поэтому даже при относительно небольшом количестве элементов в графах (порядка 100) решение задачи об изоморфизме методом полного перебора практически не реально, необходимо использовать для этой цели специальные методы.

2. ЦЕЛЬ И ПОРЯДОК РАБОТЫ

Цель работы - научится определять изоморфность двух графов.

Порядок работы:

• изучить описание работы;

• согласно своему варианту, решить заданные примеры без использования ЭВМ;

• написать и отладить программу в соответствии с заданием;

• оформить отчет.

3. ЗАДАНИЯ

3.1 Задания для ручного просчета:

Для данных графов выяснить, являются ли они изоморфными. Если да, то установить изоморфизм, в противном случае доказать, почему графы неизоморфны.

Пример.

Даны два графа. Выяснить, являются ли они изоморфными.

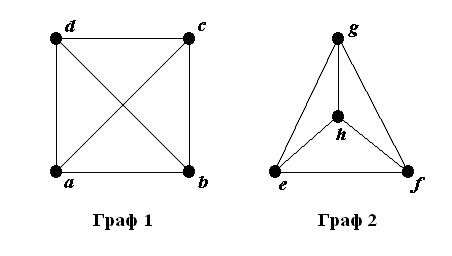
Покажем, что данные графы изоморфны.

Действительно, отображение a e, b f, c g, d h, являющееся изоморфизмом легко представить как модификацию первого графа, передвигающую вершину d в центр рисунка.

Составим матрицу смежности для первого графа:

	a	b	c	d
a	0	1	1	1
b	1	0	1	1
c	1	1	0	1
d	1	1	1	0

Составим матрицу смежности для второго графа:

	e	f	g	h
e	0	1	1	1
f	1	0	1	1
g	1	1	0	1
h	1	1	1	0

Так как соответствующие матрицы смежности одинаковы, то графы 1 и 2 изоморфны.

Решите задание вашего варианта.

Вариант 1

Вариант 2

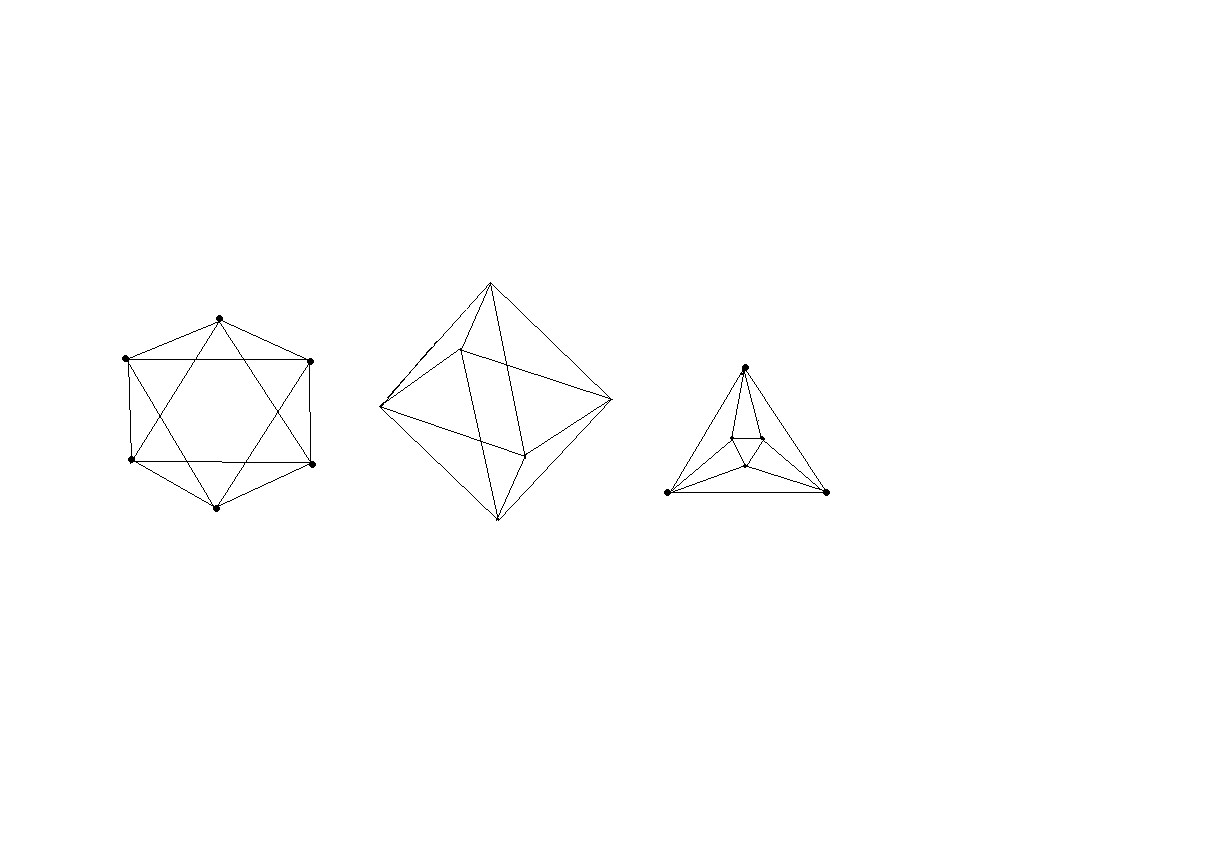Вариант 3

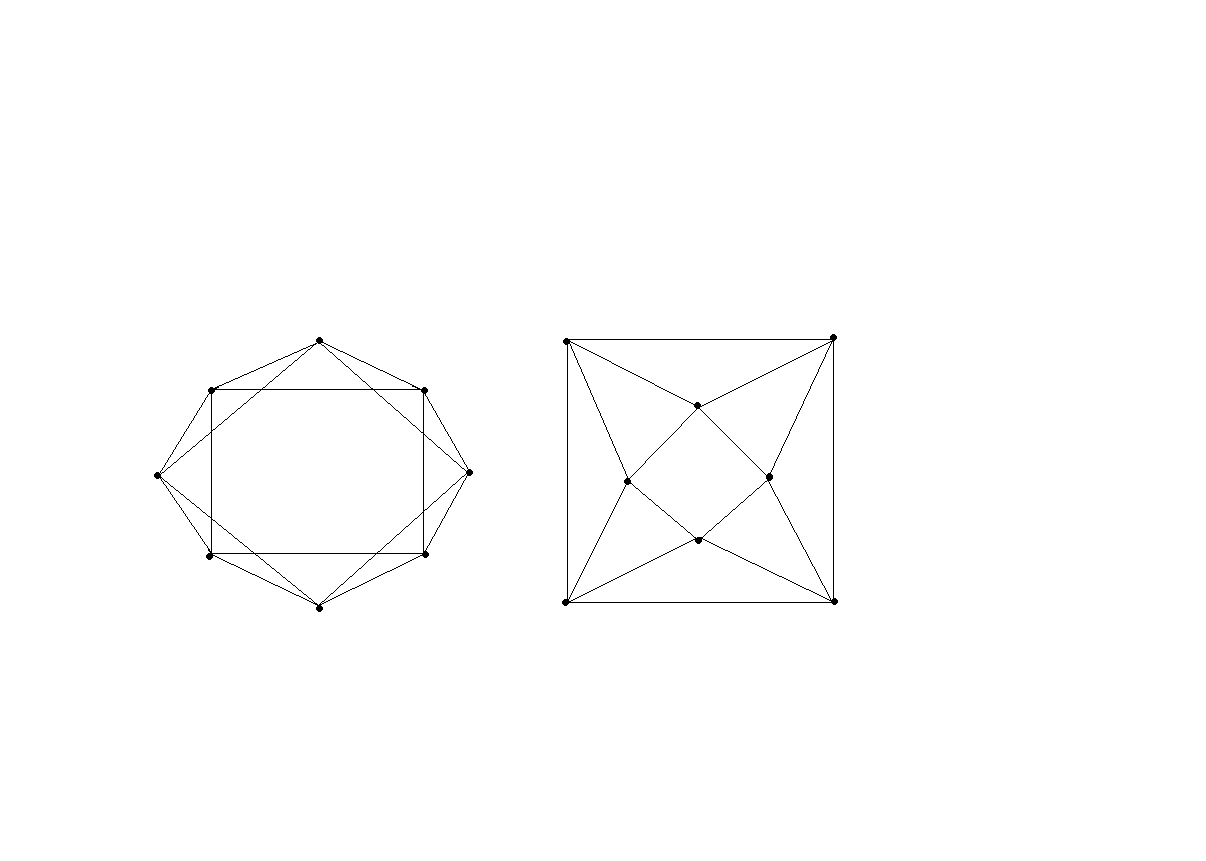Вариант 4

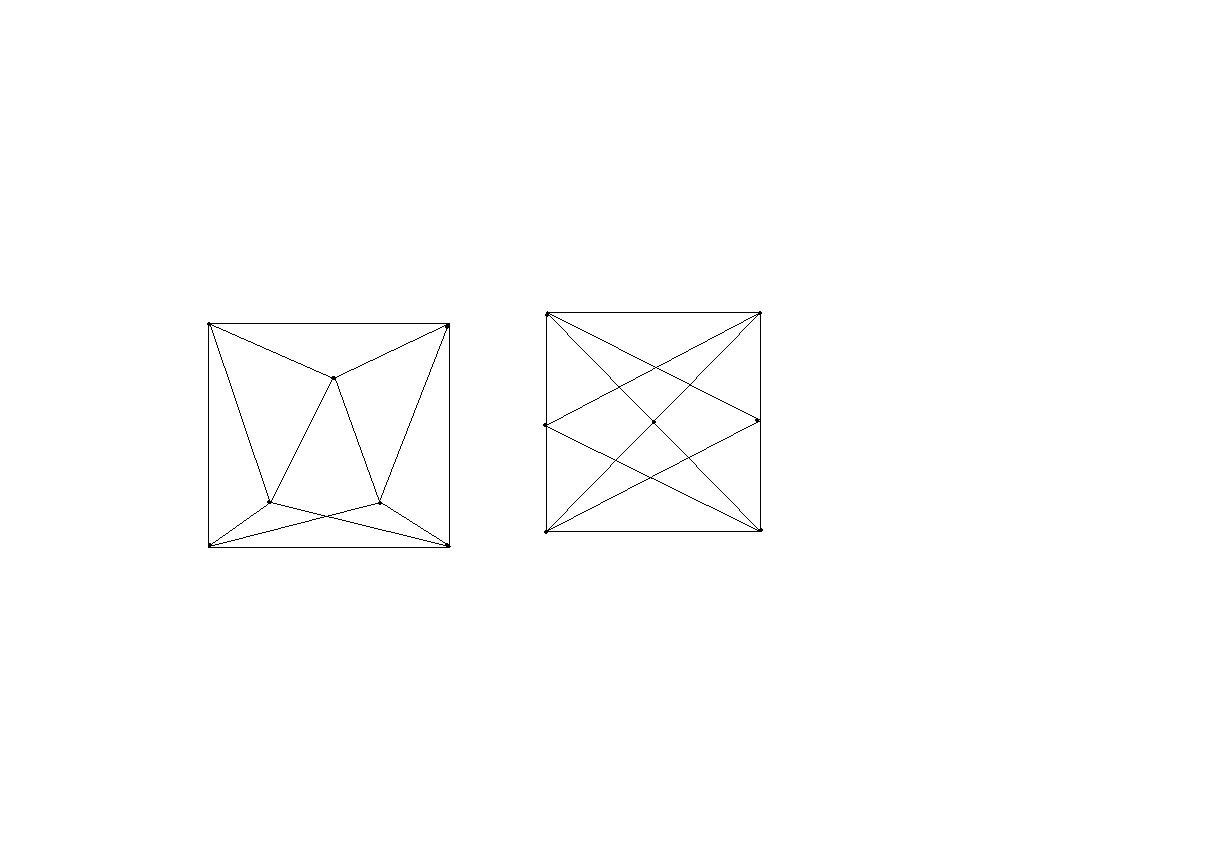Вариант 5

Вариант 6

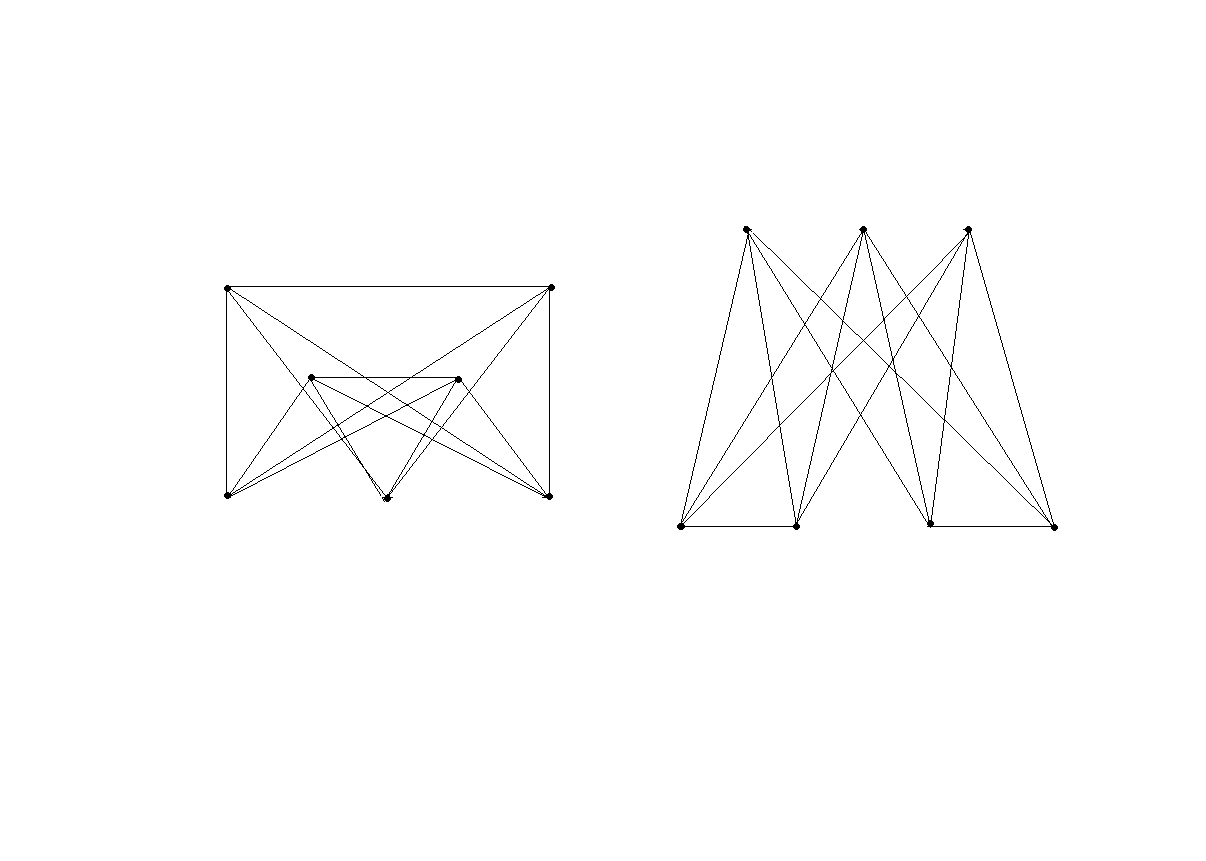Вариант 7

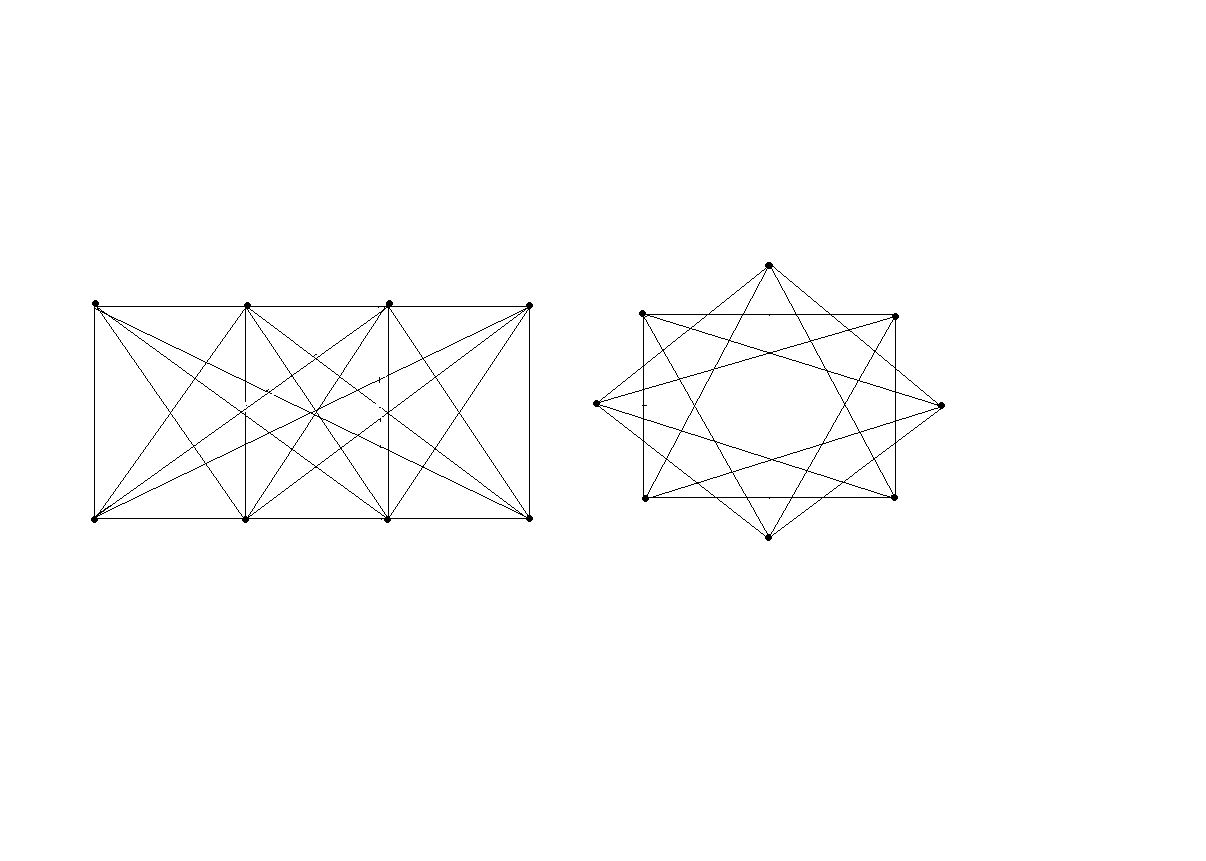Вариант 8

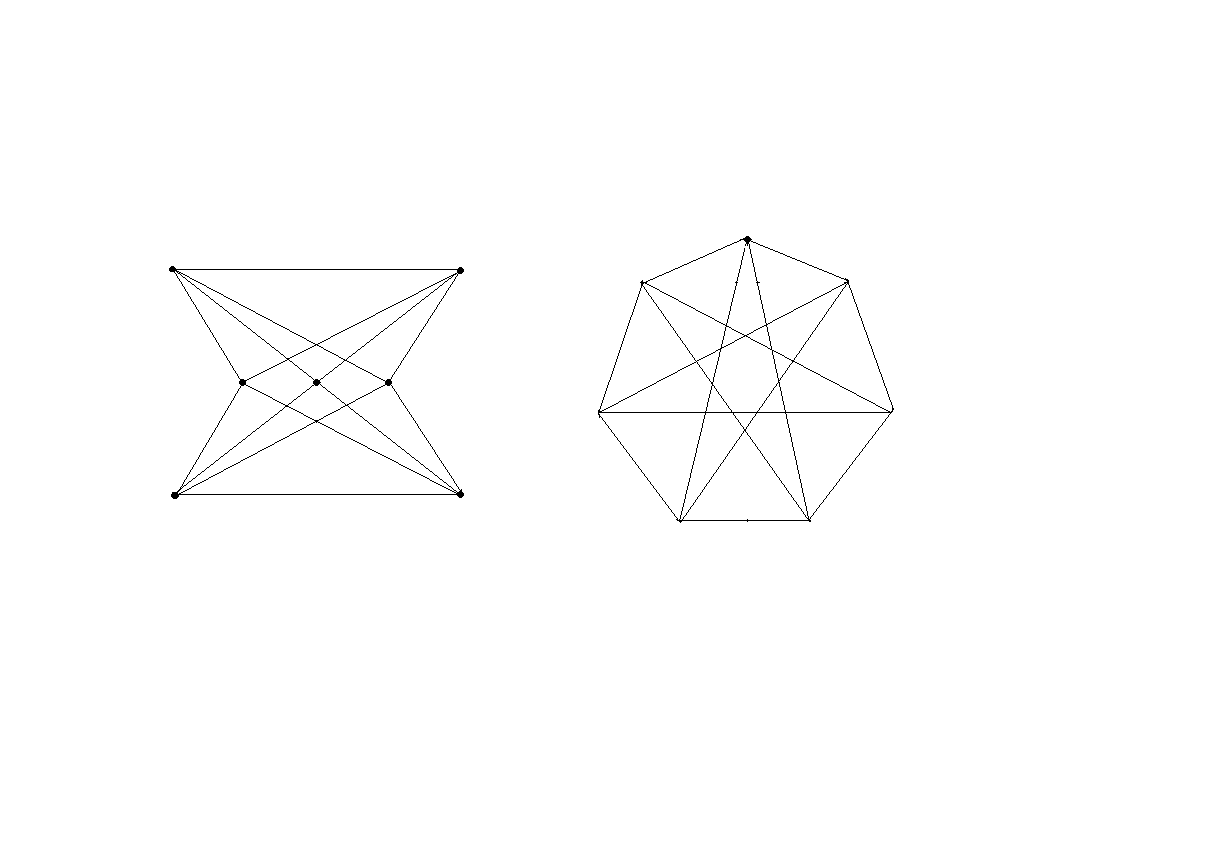Вариант 9

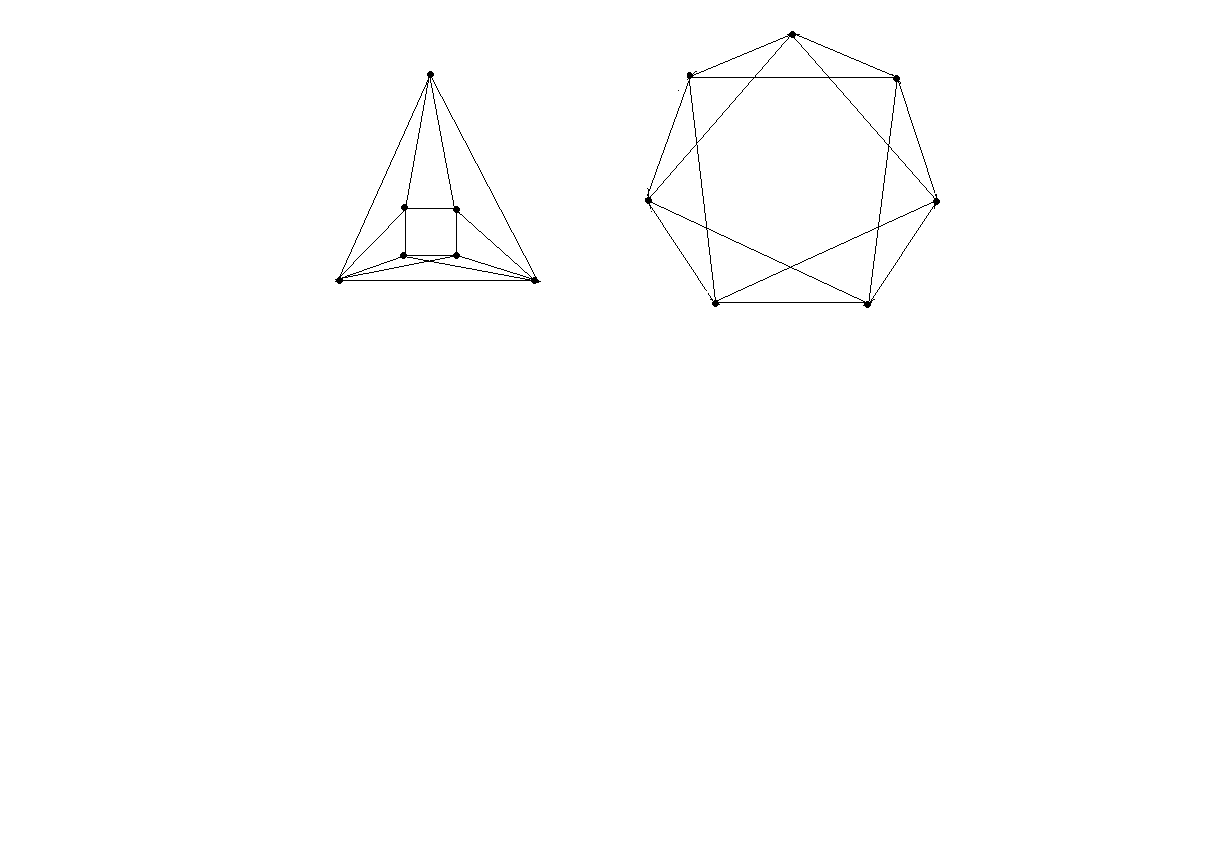
Вариант 10

3.2 Задания для вычисления с помощью программы:

Для заданных пользователем графов определить изоморфность (результатом программы является вывод «да-нет» в зависимости от заданных графов)

4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Для проверки изоморфности графов можно использовать следующий модуль (C#):

//проверка изоморфности подграфов

//int[, ,] X - матрица смежности подграфа

//int f1, int f2 - счетчики

//int k - кол-во вершин подграфа

//f1,f2 - номера подграфов

bool izomorf(int[, ,] X, int f1, int f2, int k)

{

int i, j, f;

bool b;

int n = 1;

for (i = 1; i <= k; i++) n = n * i;

int[,] M = new int[n, k]; //массив перстановок вершин,

perestan(M, k); //построение массива перестановок вершин

//сравнение подграфов с перестановкой строк и столбцов

for (f = 1; f < n; f++)

{

b = true;

for (i = 0; i < k; i++)

{

for (j = 0; j < k; j++)

if (X[f1, i, j] != X[f2, M[f, i], M[f, j]])

{

b = false; break;

}

if (!b) break;

}

if (b) return true;

}

return false;

}//izomorf

5. СОДЕРЖАНИЕ ОТЧЕТА

• наименование работы, постановку задачи;

• выбранный вариант задания;

• результаты решения задач без применения ЭВМ;

• программу решения задачи (представляется в электронном виде);

• результаты работы программы и их анализ.

6. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие графы называются изоморфными?

2. Докажите, что графы на рис. 1 изоморфны (выпишите все соответствующие вершины и ребра).

3. Дайте определение булевой матрицы.

4. Объясните понятие перестановочного подобия матриц.

5. Известно, что если графы изоморфны, то их матрицы смежности перестановочно подобны. Верно ли это утверждение наоборот?

6. В каком случае вершины u и v связны?

7. Какой граф называется подграфом?

8. Среди данных графов выберете изоморфные и неизоморфные графы.

7. ОСНОВНАЯ ЛИТЕРАТУРА

1. Ф. А. Новиков, Дискретная математика для программистов: Учеб. пособие для ВУЗов по направлениям: «Информатика и вычислительная техника»/Ф. А. Новиков – 2-е изж. – М. Спб.: Питер, 2007 – 363 с.

2. А. И. Белоусов Дискретная математика: Учеб. пособие для втузов/Белоусов А. И., Ткачев С. Б., Под ред. Зарубина В. С., Ирищенко А. П. – 3-е изд., стер. – М.: Изд-во МГТУ им. Баумана, 2004. – 743 с.

3. Оре, Ойстин Теория графов/ Пер. с англ. И. Н. Врублевской. Под редакцией Н. Н. Воробьева –2-е изд. Стереотипное. М.: Наука, 1980.-336с

4. Горбатов В. А. Дискретная математика: Учеб. для втузов В. А. Горбатов. – М.АСТ; Астель, 2003 – 447с (Высшая школа)

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. О. П. Кузнецов «Дискретная математика для инженера». Издательство: Лань, 2007 г., 400 стр.

2.Н. И. Костюкова Графы и их применение. Комбинаторные алгоритмы для программистов. Издательства: Интернет-университет информационных технологий, Бином. Лаборатория знаний, 2007 , 312 стр.

3. В. Ф. Пономарев «Дискретная математика для инженеров» Издательство: Горячая Линия - Телеком, 2009 г. Мягкая обложка, 320 стр.

4. Род Хаггарти «Дискретная математика для программистов. Discrete Mathematics for Computing». Издательство: Техносфера, 2005 г. Твердый переплет, 400 стр.

10