
дискретка_все_практики / дискретка / Раздел 1 Практика 2
.docПРАКТИЧЕСКАЯ РАБОТА №2
НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ
1. ОБЩИЕ СВЕДЕНИЯ
Рассмотрим ориентированный граф G = < V , E >.
Весом дуги графа называется вещественное число a (u , v) , поставленное в соответствие каждой дуге < u , v > E.
Если последовательность вершин v0 , v1 , . . . ,vp определяет путь в G , то его длина определяется как сумма
![]() (1)
(1)
Кратчайшим путем между двумя вершинами называется путь наименьшего веса, соединяющий эти вершины. Длину кратчайшего пути между фиксированными вершинами s , t V будем обозначать d (s , t) и называть расстоянием от s до t . Если не существует ни одного пути из s в t , то полагаем d ( s , t ) равным бесконечности.
Дадим алгоритм нахождения расстояния между вершинами. Зная расстояние, можно легко определить кратчайшие пути. Для этого достаточно отметить, что для произвольных s , t V ( s t ) существует вершина v, такая, что
![]() (2)
(2)
Далее мы можем найти вершину u , для которой
![]() (3)
(3)
и так далее.
Созданная таким образом последовательность t, v, u, . . . не содержит повторений и оканчивается вершиной s . Очевидно, что она определяет (при обращении очередности) кратчайший путь из s в t .
Таким образом, получаем следующий алгоритм:
-
begin
-
Stack := 0 ; Stack t ; v := t ;
-
while v s
-
begin
-
u := вершина , для которой D [ v ] = D [ u ] + A [ u , v ] ;
-
Stack u ;
-
v := u ;
-
end
-
end
Входными данными являются расстояния D [v] от фиксированной вершины s до всех остальных вершин v V , фиксированная вершина t, матрица весов ребер A [ u , v ] , u , v V .
Результат - Stack содержит последовательность вершин, определяющую кратчайший путь из s в t .
Большинство известных алгоритмов нахождения расстояния между двумя фиксированными вершинами s и t опирается на действия, которые в общих чертах можно представить следующим образом : при данной матрице весов дуг A u , v] , u , v V , вычисляем некоторые верхние ограничения D [ v ] на расстояния от s до всех вершин v V . Каждый раз, когда мы устанавливаем, что
![]() (4)
(4)
оценку D [v] улучшаем: D [ v ]:= D [ u ] + A [ u , v ] .
Процесс прерывается, когда дальнейшее улучшение ни одного из ограничений невозможно.
Опишем более детально один из методов нахождения расстояния от фиксированной вершины, называемой источником и обозначаемой как s, до всех остальных вершин графа - алгоритм Форда - Беллмана.
Входные данные: ориентированный граф < V , E > с n вершинами с выделенным источником s V , матрица весов дуг A [u , v] , u , v V .
Результаты: расстояния от источника до всех вершин графа:
![]() (5)
(5)
Алгоритм Форда - Беллмана:
-
begin
-
for v V do D [ v ] := A [ s , v ] ; D[ s ] :=0 ;
-
for k := 1 to n-2 do
-
for v V \ {s} do
-
for u V do D [ v ] := min ( D [ v ] , D [ u ] + A [ u , v ] )
-
End.
Рассмотрим еще один метод нахождения кратчайших путей в графе на примере алгоритма Дейкстры.
Допустим,
на некотором шаге описанного выше
алгоритма построено дерево с множеством
вершин
![]() ,
а для каждой вершины
,
а для каждой вершины
![]() известна
вершина
известна
вершина
![]() ,
на которой достигается наименьшее
значение величины
,
на которой достигается наименьшее
значение величины
![]() ,
где минимум берется по всем вершинам
,
где минимум берется по всем вершинам
![]() .
Тогда на этом шаге следует выбрать
вершину
.
Тогда на этом шаге следует выбрать
вершину
![]() с
наименьшим значением величины
с
наименьшим значением величины
![]() и
присоединить к дереву ребро
и
присоединить к дереву ребро
![]() .
После этого для каждой вершины
.
После этого для каждой вершины
![]() ,
еще не принадлежащей к дереву, значения
,
еще не принадлежащей к дереву, значения
![]() и
и
![]() уточняются
следующим образом: если
уточняются
следующим образом: если
![]() ,
то следует положить
,
то следует положить
![]() ,
,
![]() .
Вершина
.
Вершина
![]() может
рассматриваться как предполагаемый
отец вершины
может
рассматриваться как предполагаемый
отец вершины
![]() в
геодезическом дереве (если все множество
в
геодезическом дереве (если все множество
![]() состояло
бы из одной вершины
состояло
бы из одной вершины
![]() ,
то
,
то
![]() была
бы ее истинным отцом). Величина
была
бы ее истинным отцом). Величина
![]() представляет
собой оценку кратчайшего пути из
представляет
собой оценку кратчайшего пути из
![]() в
в
![]() ,
она равна весу кратчайшего из путей,
проходящих только через вершины множества
,
она равна весу кратчайшего из путей,
проходящих только через вершины множества
![]() .
После того, как вершина
.
После того, как вершина
![]() присоединяется
к дереву, значения
присоединяется
к дереву, значения
![]() и
и
![]() больше
не изменяются,
больше
не изменяются,
![]() является
отцом вершины
является
отцом вершины
![]() в
геодезическом дереве, а
в
геодезическом дереве, а
![]() .
В целом алгоритм можно представить
следующим образом:
.
В целом алгоритм можно представить
следующим образом:
Алгоритм Дейкстры:
-
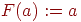
-

-
for
 do
do
 ;
;

-
while
 do
do
-
выбрать вершину
 с
наименьшим значением
с
наименьшим значением
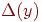
-
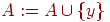
-
for
 do
do -
if
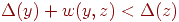
-
then
 ,
,
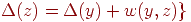
![]() Например, в алгоритме
Джонсона
используется алгоритм
Форда-Беллмана
и алгоритм
Дейкстры,
реализованные в виде подпрограмм. Ребра
хранятся в виде списков смежных вершин.
Алгоритм возвращает обычную матрицу D
= dij
размером
Например, в алгоритме
Джонсона
используется алгоритм
Форда-Беллмана
и алгоритм
Дейкстры,
реализованные в виде подпрограмм. Ребра
хранятся в виде списков смежных вершин.
Алгоритм возвращает обычную матрицу D
= dij
размером
![]() ,
где
,
где
![]() ,
или выдает сообщение о том, что входной
граф
содержит цикл с отрицательным весом.
,
или выдает сообщение о том, что входной
граф
содержит цикл с отрицательным весом.
Алгоритм Джонсона:
//Строится граф G'
if
Bellman_Ford![]() = FALSE
= FALSE
then print «Входной граф содержит цикл с отрицательным весом»
else
for
для каждой
![]()
do
присвоить величине h(v)
значение
![]() ,
,
вычисленное алгоритмом Беллмана — Форда
for
для каждого ребра
![]()
do
![]()
for
для каждой вершины
![]()
do вычисление с помощью алгоритма Дейкстры
![]() величин
величин
![]()
для
всех вершин
![]()
for
для каждой вершины
![]()
do
![]()
return D
2. ЦЕЛЬ И ПОРЯДОК РАБОТЫ
Цель работы - научится находить кратчайший путь в графе, применяя выбранный Вами алгоритм.
Порядок работы:
-
изучить описание работы;
-
согласно своему варианту, решить заданные примеры без использования ЭВМ;
-
написать и отладить программу в соответствии с заданием;
-
оформить отчет.
3. ЗАДАНИЯ
3.1 Задания для ручного просчета:
Пример: найти кратчайший путь от вершины X к вершине Y в графе:



 2 5
2 5



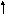
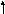
1

 5 6
5 6

 7 8
7 8

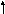
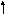
11 3 3




 10 8
10 8

Найти кратчайший путь от вершины X к вершине Y в графе:
Граф № 1:
1.X = 4 , Y = 6
2.X = 1 , Y = 9
3.X = 1 , Y = 6
4.X = 5 , Y = 7
5.X = 3 , Y = 4
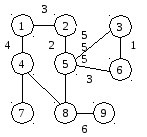
Граф № 2:
6. X = 1 , Y = 8
7. X = 1 , Y = 3
8. X = 2 , Y = 7
9. X = 2 , Y = 9
10. X = 3 , Y = 8
Граф № 3:
11. X = 1 , Y = 3
12. X = 1 , Y = 8
13. X = 2 , Y = 7
14. X = 3 , Y = 4
15. X = 4 , Y = 9
1.
3
2.

3 .
.
3.2 Задания для вычисления с помощью программы:
Написать программу, находящую кратчайший путь между вершинами X и Y в данном графе.
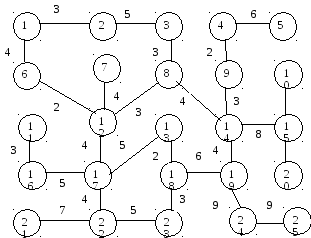
Варианты:
-
X = 1 , Y = 8
-
X = 1 , Y = 18
-
X = 7 , Y = 24
-
X = 9 , Y = 17
-
X = 2 , Y =12
-
X = 8 , Y = 23
-
X = 8 , Y = 13
-
X = 3 , Y = 13
-
X = 5 , Y = 13
-
X = 11 , Y = 18
-
X = 12 , Y= 20
-
X = 2 , Y = 7
-
X =17 , Y =25
-
X = 4 , Y =1
-
X = 15 , Y =22
4. МЕТОДИЧЕСКИЕ УКАЗАНИЯ
-
Для нахождения массива расстояний от заданной точки до остальных вершин можно использовать эту процедуру:
Procedure MakeL;
Begin
for i:=0 to n-1 do L[1,i]:=0;
for i:=2 to n do L[i,0]:=max;
for k:=1 to n-1 do
for i:=2 to n do
begin
L[i,k]:=max;
for j:=1 to n do
if C[j,i]+L[j,k-1]<=L[i,k] then
begin
L[i,k]:=C[j,i]+L[j,k-1];
Path[i,k]:=j;
end
end
End { MakeL };
Здесь C - матрица весов дуг ,
Path - матрица путей ,
max - константа , при равенстве пути которой он считается равным бесконечности.
-
Рассмотрим алгоритм Форда-Беллмана (нахождение минимальных путей в графе) на языке С++
class Spisok { private: int A[MaxNodes][MaxNodes]; //Матрица весов дуг. int D[MaxNodes]; //Матрица расстояний от источника до //всех вершин графа. svqz Stack; //Указатель на рабочий стек. void UDALENIE (svqz *, int *); void W_S (svqz *, int); public: Spisok() {Stack = NULL;} void Vvod_Ves(); void Reshenie (); }; void main () { Spisok A; A.Vvod_Ves(); A.Reshenie(); }; void Spisok::Reshenie () { int S; // Начальная вершина пути (источник). int T; // Конечная вершина пути. int u,v; int i,j,k; svqz UkZv; cout << Decode_Win_to_DOS("Введите источник: "); cin >> S; S–; //Инициализация. for (i=0;i<MaxNodes;i++) D[i] = A[S][i]; D[S] = 0; //Вычисление матрицы расстояний от //источника до всех вершин графа. for (k=0;k<MaxNodes-2;k++) for (i=0;i<MaxNodes;i++) if ( i!=S ) for (j=0;j<MaxNodes;j++) if ( D[i] > D[j]+A[j][i] ) D[i] = D[j]+A[j][i]; //Вывод матрицы расстояний от источника //до всех вершин графа. cout << Decode_Win_to_DOS("Матрица расстояний: \n"); for (i=0;i<MaxNodes;i++) cout << D[i] << " "; cout << endl; // —————————————————– // Нахождение кратчайшего пути из S в T с использованием // построенной матрицы расстояний. // —————————————————– cout << Decode_Win_to_DOS("Введите конечную вершину пути: "); cin >> T; T–; W_S (&Stack,T); v = T; while ( v!=S ) { for (i=0;i<MaxNodes;i++) if ( D[v]==D[i]+A[i][v] ) u = i; W_S (&Stack,u); v = u; } //Вывод кратчайшего пути на экран дисплея. cout << Decode_Win_to_DOS("Кратчайший путь: "); UkZv = Stack; while ( UkZv != NULL ) { cout << UkZv->Element << " "; UkZv = UkZv->Sled; } cout << endl; system("pause"); } void Spisok::Vvod_Ves() //Ввод матрицы весов дуг заданного графа. { cout << Decode_Win_to_DOS("Вводите элементы матрицы весов дуг по строкам:\n"); for (int i=0;i<MaxNodes;i++) for (int j=0;j<MaxNodes;j++) { cout << Decode_Win_to_DOS("Введите A[") << (i+1) << "," << (j+1) << Decode_Win_to_DOS("]: "); cin >> A[i][j]; if ( A[i][j]==0 ) A[i][j] = B; } } void Spisok::W_S (svqz *stk, int Elem) //Помещение Elem в стек stk. { svqz q=new (Zveno); (*q).Element = Elem; (*q).Sled = *stk; *stk = q; } void Spisok::UDALENIE (svqz *stk, int *Klad) //Удаление звена из стека, заданного указателем *stk. //Значение информационного поля удаляемого звена сохраняется в параметре Klad. { svqz q; if (*stk==NULL) cout<<Decode_Win_to_DOS("Попытка выбора из пустого стека!\n"); else { *Klad = (**stk).Element; q = *stk; *stk = (**stk).Sled; delete q; } }
-
Алгоритм Форда-Беллмана предназначен для поиска кратчайшего пути, а также для обхода в глубь для поиска всех путей. Реализация этого алгоритма на языке Pascal представлен ниже.
var a : array [1..20,1..20] of word;{матрица смежности}
c, pred, fl, d : array [1..20] of word;{
c – массив кратчайших расстояний
pred – массив предыдущих вершин
fl – массив флагов
d – массив для записи пути
}
i, j, k, n, first, last : byte;
f : text;{переменная для открытия файла в .txt}
{процедура обхода графа вглубь – для поиска всех путей}
Procedure Dfs(x : word);
var i : byte;{локальная переменная}
begin
if x=last then {если конечная вершина, то выводим путь}
begin
write(first,' ');
for i:=1 to j do {выводим путь}
write(d[i],' ');
writeln;
exit;{выводим из процедуры}
end;
fl[x]:=1;{помечаем, что были в вершине}
for i:=1 to n do
if (fl[i]=0)and(a[x,i]<>32767) then
begin
inc(j);
d[j]:=i;{записываем в путь вершину}
dfs(i);{vizivaemsya ot i-oy vershini}
dec(j);
end;
fl[x]:=0;{помечаем, что вершина свободна}
end;
{основная программа}
begin
assign(f,'in.txt');{открываем файл для чтения}
reset(f);
readln(f, n);{считываем количество вершин}
for i := 1 to n do
for j := 1 to n do
read(f, a[i,j]);{считываем матрицу смежности}
writeln('Matrix:');
for i:=1 to n do {выводим матрицу на экран}
for j:=1 to n do
if j=n then writeln(a[i,j]) else write(a[i,j],' ');
for i:=1 to n do {заменяем нули бесконечностью}
for j:=1 to n do
if a[i,j]=0 then a[i,j]:=32767;
writeln('Vvedite 1 vershiny');
readln(first);
writeln('Vvedite 2 vershiny');
readln(last);
close(f);{zakrivaem file in.txt}
for j := 1 to n do
begin
c[j] := a[first,j];{записываем начальные значения}
if a[first,j] < 32767 then
pred[j] := first;
end;
for i := 3 to n do
for j := 1 to n do
if j <> first then
for k := 1 to n do {если не бесконечность и путь более выгодный}
if (c[k] < 32767) and (c[k] + a[k,j] < c[j]) then
begin
c[j] := c[k] + a[k,j];{записываем новое значение}
pred[j] := k;{записываем предыдущую вершину}
end;
if c[last] = 32767 then writeln('Net putey') else
begin
writeln;
writeln('Kratchaishiy put:');
write(first,' ');
i := last;
k := 1;
while i <> first do {в обратном порядке обходим путь }
begin
d[k] := i;{записываем путь в массив}
k := k + 1;
i := pred[i];
end;
for i := k - 1 downto 1 do {выводим кратчайший путь}
write(d[i],' ');
writeln;
writeln('Vse puti:');
j:=0;
Dfs(first);{вызываем процедуру поиска всех путей}
end;
readln; {ждем нажатия клавиши}
end.
-
Алгоритм определения кратчайшего пути между вершинами графа также может быть описан следующим модулем программы:
unit MinLength;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Dialogs,
StdCtrls,IO,Data,AbstractAlgorithmUnit; type
TMinLength = class(TAbstractAlgorithm) private
StartPoint:integer;
EndPoint:integer;
First:Boolean;
Lymbda:array of integer; function Proverka:Boolean; public procedure Make; end;
var
MyMinLength: TMinLength; implementation
uses MainUnit, Setting; procedure TMinLength.Make; var i ,j : integer;
PathPlace,TempPoint:Integer; flag:boolean; begin with MyData do begin
StartPoint:=MyIO.FirstPoint;
EndPoint:=MyIO.LastPoint;
SetLength(Lymbda,Dimension+1);
SetLength(Path,Dimension+1); for i:=1 to Dimension do
Lymbda[i]:=100000;
Lymbda[StartPoint]:=0; repeat for i:=1 to Dimension do for j:=1 to Dimension do if Matrix[i,j]=1 then if ( ( Lymbda[j]-Lymbda[i] ) > MatrixLength[j,i] ) then Lymbda[j]:=Lymbda[i] + MatrixLength[j,i]; until Proverka ;
Path[1]:= EndPoint ; j:=1;
PathPlace:=2; repeat
TempPoint:=1;
Flag:=False; repeat if ( Matrix[ Path[ PathPlace-1 ],TempPoint] =1 )and (
Lymbda[ Path[ PathPlace-1] ] =
( Lymbda[TempPoint] + MatrixLength[ Path[PathPlace- 1 ], TempPoint] ) ) then Flag:=True else Inc( TempPoint ); until Flag;
Path[ PathPlace ]:=TempPoint; inc( PathPlace );
MyIO.DrawPath(Path[ PathPlace-2 ],Path[ PathPlace -1],true);
// ShowMessage('f'); until(Path[ PathPlace - 1 ] = StartPoint);
// MyIO.DrawPath(Path[ PathPlace-1 ],Path[ PathPlace ],true); end; end; function TMinLength.Proverka:Boolean; var i,j:integer;
Flag:boolean; begin i:=1;
Flag:=False;
With MyData do begin repeat j:=1; repeat if Matrix[i,j]=1 then if ( Lymbda[j]-Lymbda[i] )>MatrixLength[j,i]then Flag:=True; inc(j); until(j>Dimension)or(Flag); inc(i); until(i>Dimension)or(Flag);
Result:=not Flag; end; end;
end.
5. СОДЕРЖАНИЕ ОТЧЕТА
-
наименование работы, постановку задачи;
-
выбранный вариант задания;
-
результаты решения задач без применения ЭВМ;
-
программу решения задачи (представляется в электронном виде);
-
результаты работы программы и их анализ.
6. КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Что называется весом дуги?
-
Что такое кратчайший путь между двумя вершинами?
-
Как определяется длина пути в графе?
-
Что называется расстоянием между фиксированными вершинами графа?
-
Чему принимается равным расстояние d (s , t) между двумя фиксированными вершинами графа s и t , если не существует пути из s в t?
-
Опишите алгоритм нахождения расстояния между двумя фиксированными вершинами.
-
Какая вершина называется источником?
-
Опишите алгоритм Форда - Беллмана.
-
Опишите алгоритм Дейкстры.
10) Опишите алгоритм Джонсона.
7. ОСНОВНАЯ ЛИТЕРАТУРА
-
О. П. Кузнецов, Г. М. Адельсон-Вельский «Дискретная математика для инженера». - М.: Энергоатомиздат, 1988 – 479, [1] с.: кл., 22 см.
-
Ф. А. Новиков, Дискретная математика для программистов: Учеб. пособие для ВУЗов по направлениям: «Информатика и вычислительная техника»/Ф. А. Новиков – 2-е изж. – М. Спб.: Питер, 2007 – 363 с.
-
А. И. Белоусов Дискретная математика: Учеб. пособие для втузов/Белоусов А. И., Ткачев С. Б., Под ред. Зарубина В. С., Ирищенко А. П. – 3-е изд., стер. – М.: Изд-во МГТУ им. Баумана, 2004. – 743 с.
-
А. А. Зыков Основы теории графов – М., Наука, 1987. – 380, [1] с. кл.; 23 см.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Ю. П. Шевелев «Дискретная математика».
Издательство: Лань, 2008 г. Твердый переплет, 592 стр.
2. С. В. Яблонский «Введение в дискретную математику».
Издательство: Высшая школа, 2008 г. Твердый переплет, 384 стр.
3. В. Ф. Пономарев «Дискретная математика для инженеров»
Издательство: Горячая Линия - Телеком, 2009 г. Мягкая обложка, 320 стр.
4. Род Хаггарти «Дискретная математика для программистов. Discrete Mathematics for Computing».
Издательство: Техносфера, 2005 г. Твердый переплет, 400 стр.
