Theoretical Calculations and Numerical Modeling 385

microscopic nonvolatile liquid droplet on a homogeneous solid substrate. The substrate was assumed to be continuous without atomic structure and exerting a long-range Lennard-Jones potential on liquid particles in the droplet. The molecular film was observed to spread initially with nearly constant speed, crossing over later to diffusive spreading. Cheng and Ebner[342] used the Monte Carlo method to implement a 2-D non-volatile Ising-lattice-gas model with particle-number conservation. The dynamics of droplet spreading on a solid surface was simulated with different substrate-droplet longrange attractive-potential strengths and under both wetting and nonwetting conditions. This model was deemed to be an improvement over the previous horizontal solid-on-solid model.

5.4.2Modeling of Droplet Deformation and Solidification on a Cold Surface

Deformation and solidification of a single molten metal droplet on a cold surface are of particular importance in thermal spray processes. Madejski[401] developed a simplified flow model, including inertial, viscous and surface tension effects, to predict the final splat diameter and height. Solidification during droplet spreading was determined by incorporating the 1-D Stefan solution into the macroscopic flow model. A recent analytical study[157] modified some of the assumptions of Madejski’s model and addressed the effects of different solid fractions of a droplet prior to impact. Using Madejski’s model, however, the details of the transient deformation process during droplet spreading, especially during the interaction of multiple droplets, cannot be determined.

Trapaga and Szekely[515] conducted a mathematical modeling study of the isothermal impingement of liquid droplets in spray processes using a commercial CFD code called FLOW-3D. Their model is similar to that of Harlow and Shannon[397] except that viscosity and surface tension were included and wetting was simulated with a contact angle of 10°. In a subsequent study,[371] heat transfer and solidification phenomena were also addressed. These studies provided detailed

386 Science and Engineering of Droplets

information of the spreading process of a single droplet on a flat surface and related the final splat diameter to operation parameters such as initial droplet velocity, diameter and material properties. The numerical results revealed that the liquid film created on the substrate surface by an impinging droplet spreads radially at a velocity about three times the droplet impact velocity, in agreement with the experimental data of Shi and Dear.[637] The final splat size was shown not sensitive to the liquid surface tension under the operation conditions typical of plasma spray applications. This is especially true for cases where a liquid wets the target substrate. Breakup of a splat of a non-wetting liquid was also reported, although the results were dependent on the mesh size used. Generally, the numerical results showed the same trends as those found by Madejski[401] except for a slightly smaller splat diameter. Trapaga and Szekely also compared their modeling results to their own experimental data for millimeter-sized droplets and indicated that the existence of a contact resistance does not greatly influence the final splat size. However, Dykhuizen[390] argued that this conclusion would not likely be valid for thermal spray applications. In addition, only preliminary numerical results were presented in these studies regarding the interactions of two droplets on a flat surface, a single droplet into a liquid pool and onto a fiber.

Watanabe et al.[517] conducted numerical modeling of deformation and solidification of a molten droplet onto a cold substrate using the Simplified Marker and Cell (SMAC) algorithm and obtained results very similar to those of Trapaga and Szekely.[515] The numerical simulation showed that solidification occurs immediately after deformation, and the solidification time is two orders of magnitude longer than the deformation time. The normalized deformation time (time corresponding to 90% deformation), tmax,d, and solidification

time, tmax,s, are both proportional to the 0.2 power of the Reynolds number:

Theoretical Calculations and Numerical Modeling 387

Using a finite element method, Bertagnolli et al.[518] simulated the simultaneous spreading and solidification of a ceramic droplet on a rigid substrate under plasma spray conditions. Numerical simulations of similar phenomena have also been conducted by Pasandideh-Fard et al.[366][367][638] using an enthalpy approach and the SOLA-VOF method.[639] A comparison of the computer generated images with photographs of a spreading droplet showed that the numerical model could predict, with reasonable accuracy, the droplet shape and contact diameter during spreading and at equilibrium,[366] as well as during simultaneous deformation and solidification.[367] The model, however, overpredicted the droplet contact diameter during recoiling.[366]

A series of theoretical and numerical studies of droplet spreading on a surface have been performed by Fukai et al.,[341][362] Kang et al.,[381] Zhao et al.,[368] and Waldvogel and Poulikakos.[50] Zhao et al.[368] investigated the fluid dynamics and heat transfer phenomena during the impingement of a single liquid metal droplet on a cold surface and a single water droplet on a hot substrate. In their modeling study, the basic conservation equations in the Lagrangian formulation were solved numerically by extending the model and associated numerical methodologies of Fukai et al.[341] based on a finite element technique. A deforming mesh was utilized to accurately simulate the large deformations and to accommodate the domain non-uniformity characteristic of droplet spreading processes. The temperature variations in both the droplet and substrate were calculated during droplet deformation. The effects of thermophysical properties of the droplet and substrate, droplet diameter and impact velocity on the fluid dynamics and heat transfer during droplet spreading were examined. The results showed that the impact dynamics is characterized by droplet spreading, recoiling and oscillations. Droplet spreading is retarded and finally halted by the action of the surface tension and viscosity forces. Subsequently, the liquid flow reversal (recoiling) sets in and the main

388 Science and Engineering of Droplets

flow is directed toward the axis of symmetry. The fluid motion in the first spreading-recoiling cycle is substantially stronger than that in subsequent oscillations, suggesting that within the impact velocity range considered, most of the droplet impact energy is dissipated within the first cycle. The duration of the spreading motion in the first cycle is considerably shorter than the duration of the recoiling motion. The spreading and recoiling motions depend upon the initial droplet velocity and properties. The occurrence of the recoiling and mass accumulation around the splat periphery were deemed to be standout features of this type of numerical simulations under the impact conditions considered. The recoiling leads to a non-mono- tonic dependence of the maximum splat diameter on time. Accordingly, the maximum splat thickness does not always occur at the axis of symmetry, but instead at the splat periphery in the late stage of spreading. The predicted temperature distribution in a molten metal droplet during quenching exhibits strong 2-D features. Convection effects on the temperature evolution were found to be important for the entire history of spreading. These effects sometimes result in a practically radial temperature variation in the late stage of spreading, particularly in the cases of high impact velocities, although the splat diameter is many times larger than the splat thickness. The fluid temperature at the spreading front is substantially lower than the temperature at the splat center. Thus, solidification may be expected to initiate around the periphery of the flattening droplet in the neighborhood of the contact line and advance towards the splat center. Under the impact conditions considered, the heat transfer time scales were found to be comparable to the deformation time scales.

Waldvogel and Poulikakos[50] extended the model and numerical techniques of Zhao et al.[368] by incorporating solidification and droplet-substrate contact resistance in the heat transfer model. They conducted both theoretical and experimental studies on the impact and solidification of molten solder droplets on a multilayer substrate. The theoretical model was based on the Lagrangian formulation, and accounted for a host of thermal-fluid phenomena,

Theoretical Calculations and Numerical Modeling 389

including surface tension and heat transfer with solidification. Deforming finite elements with integrated automatic mesh generation were utilized to accommodate the large deformations that develop during the computations. The influences of initial droplet temperature, impact velocity, thermal contact resistance and initial substrate temperature on droplet spreading, final deposit shape, and onset and completion times of solidification were examined in the simulations. Many non-intuitive results were obtained, such as the non-mono- tonic dependence of solidification time on variations of many parameters considered. The modeling results also suggested strong coupling between the droplet dynamics and solidification behavior.

It should be noted that it is difficult to obtain models that can accurately predict thermal contact resistance and rapid solidification parameters, in addition to the difficulties in obtaining thermophysical properties of liquid metals/alloys, especially refractory metals/alloys. These make the precise numerical modeling of flattening processes of molten metal droplets extremely difficult. Therefore, experimental studies are required. However, the scaling of the experimental results for millimeter-sized droplets to micrometer-sized droplets under rapid solidification conditions seems to be questionable if not impossible,[390] while experimental studies of micrometer-sized droplets under rapid solidification conditions are very difficult, and only inconclusive, sparse and scattered data are available.

5.4.3Modeling of Interactions of Multiple Droplets on Flat and Non-Flat Surfaces

Most previous modeling studies focused on the spreading process of a single droplet on a flat surface, not taking into account the influence of surface roughness and interactions of multiple droplets. Under the practical conditions in spray deposition and thermal spray processes, the physical phenomena of droplet spreading and consolidation take place at a microscopically rough and non-flat surface on a target substrate. It is widely accepted that the most critical factors governing the quality of as-sprayed materials are

390 Science and Engineering of Droplets

bonding and porosity which are directly related to the interactions of droplets on the target substrate surface. Therefore, it is necessary to investigate the transient deformation behavior of molten droplets during impingement onto a rough and non-flat surface, including the interactions of multiple droplets. It is also desired to ascertain the effects of process parameters, such as substrate surface condition, initial droplet velocity and diameter, as well as material properties, on the deformation and interactions. In addition, the mechanisms of the formation and evolution of various types of porosity need to be addressed.

Recently, Liu et al.[18][51][52][144][338][339][378][379][388][389] per-

formed extensive modeling studies on droplet impingement processes. In their work, the deformation and interactions of multiple droplets on both flat and non-flat surfaces were numerically investigated. The governing equations describing the fluid flow and interactions during substrate impact of droplets were composed of the continuity equation, the complete Navier-Stokes equations for transient, axisymmetric, viscous, incompressible fluid flow, including surface tension effects, and the equations for the VOF function. The full Navier-Stokes equations in primitive variables were solved on an Eulerian, rectangular, staggered mesh in cylindrical geometry using the extended SOLA-VOF method.[530][639] Free surfaces were represented with data of the VOF function on the numerical mesh. Surface tension was modeled as a volume force derived from the continuum surface force model.[530] The numerical calculations were conducted by modifying a computer code called RIPPLE developed by Kothe et al.[530] at Los Alamos National Laboratory. A two-domain method was used to simulate the thermal field and solidification in the flattening droplets and to track the moving solid-liquid interfaces. The Stefan solution of solidification problem was incorporated into a twophase flow continuum model to simulate the liquid flow with a growing solid layer. The numerical results were used to determine the exact motion, solidification and interactions of droplets with arbitrary free surfaces and solid-liquid interfaces on the deposition substrates of various surface morphologies. The micro-porosity was quantitatively

Theoretical Calculations and Numerical Modeling 391

calculated from the VOF function data based on an algorithm developed by Liu et al.[52]

The modeling studies by Liu et al.[18][51][52][144][338][339][378]

[379][388][389] not only provided detailed information on spreading and interactions of multiple droplets on flat and non-flat surfaces, but also improved the understanding of the effects of important process parameters on the spreading and interactions of multiple droplets. In addition, the numerical results provided insight into the formation and evolution of vortices and the breakup and ejection of liquid from deposition surface during impingement of multiple droplets. Therefore, these studies formed a useful basis for exploring the mechanisms that govern the micro-porosity evolution and for correlating the sticking efficiency of droplets on the deposition surface to thermal, dynamic and geometry conditions during spray forming. Moreover, the work established a good starting point for modeling droplet spreading with simultaneous solidification.[390] As solidification models are improved, incorporating thermal contact resistance and nucleation delay, more accurate predictions of droplet impact dynamics may become possible.

The numerical simulations[388][389] predicted that the liquid film created on a substrate surface by an impinging droplet spreads radially at a velocity twice the droplet impact velocity. A fully liquid droplet impinging onto a solid particle on a flat surface leads to the formation of macro-pores between the particle boundary and the surface (Fig. 5.10). Multiple fully liquid droplets striking onto a solid particle on a flat surface substantially eliminate the macro-pores, but simultaneously produce vortices within the liquid, as well as breakup and ejection of the liquid. Multiple fully liquid droplets striking onto multiple solid particles on a flat surface not only lead to the vortices and ejection of the liquid, but also to the formation of the macro-pores due to the large solid fraction. Therefore, increasing the liquid fraction in the spray may reduce the macro-porosity significantly. However, an excessive liquid fraction in the spray may decrease the sticking efficiency as a result of the increased ejection of the liquid from the deposition surface. Detailed descriptions of various mechanisms of

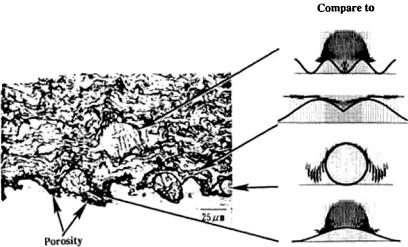
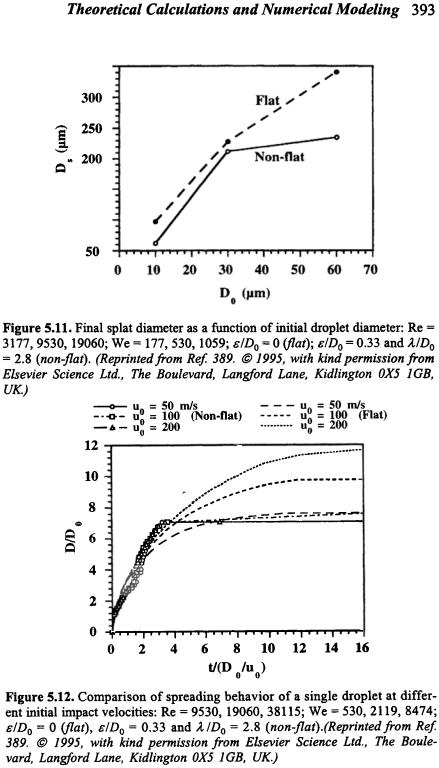
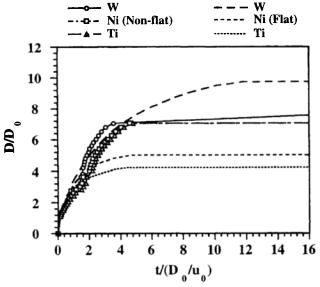
Theoretical Calculations and Numerical Modeling 395

40, the droplet spreads out into a thin liquid film on the surface with little or no normal velocity component.[641] This criterion, as suggested by Wachters and Westerling,[641] has been used by other researchers in subsequent modeling studies.[574][599] The degree of droplet-surface wetting depends on many factors, such as surface temperature, material and roughness, and droplet impingement angle, etc.[641] At high temperatures, film boiling may set in.

Naber and Reitz[599] proposed three impingement models:

(a)Stick model: Droplets adhere to wall surface at the impingement location and continue to vaporize.

(b)Reflect model: Droplets that impinge the wall rebound with their tangential and normal velocity components unchanged but an opposite sign for the normal velocity component.

(c)Jet model: Droplets glide along the wall surface.

Computed spray structure showed that a wall-jet emanates radially outward from the spray impingement site. The leading edge of the jet contains a large vortex. Small droplets are deflected away from the wall by the gas wall-jet flow, forming a wall spray with the small droplets entrained in the gas wall-jet vortex. Large droplets that impinge on the wall with high momentum move along the wall. The spray-wall interaction is weak for large impingement angles (i.e., angle between spray jet centerline and wall surface normal). Comparison of the model predictions with experimental data[644] suggested that the jet model agrees best with the experiments.

Gonzalez et al.[574] modified these models for cold-starting diesel engine applications. Naber and Farrell[645] studied hydrodynamics of droplet impingement on a heated surface under the diesel engine conditions where the combustion chamber pressures are higher than the critical pressure of the impinging fuel. They showed that the formation of a liquid film on the wall surface influences heat transfer and vaporization rates. For surface temperatures below the critical temperature, wall-wetting takes place even at supercritical pressures. For surface temperatures above the critical temperature, non-wetting

396 Science and Engineering of Droplets

(Leidenfrost) phenomenon occurs. For diesel engines, the wallwetting regime is the appropriate hydrodynamic regime. Eckhause and Reitz[646] formulated a spray-wall heat transfer model based on these findings and simulated the breakup of droplets during impingement on a wall using the KIVA code.[555] In the flooded regime, heat transfer was modeled by means of the boundary layer correlations. In the non-flooded regime, heat transfer was modeled with the correlations for individual droplets impinging on a surface.

In a series of numerical modeling studies of diesel spray impingement on a flat wall, Senda et al.[422] fine-tuned the impingement models developed by Naber and Reitz.[599] In the modeling, Senda et al. considered the following phenomena: (a) formation of fuel film on the wall, (b) breakup of the film and impinging droplets, (c) heat transfer from the wall to the droplets, (d) droplet-droplet and dropletfilm interactions, and (e) dispersion of secondary droplets. They proposed new sub-models for droplet deformation, heat transfer, fuel film formation and dispersion process of an impinging spray near a flat wall, and incorporated the sub-models into the KIVA code[555] to simulate the spray impingement on both low-temperature and hightemperature walls. The numerical results showed both upward and radial dispersions of secondary droplets due to the breakup and splashing of impacting droplets during the spray impingement.