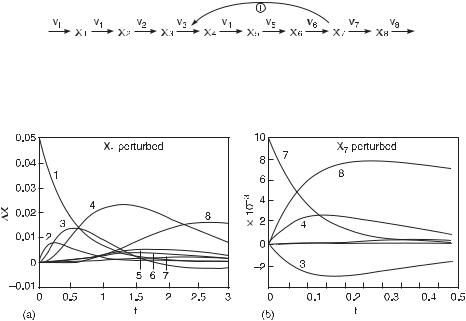
Fig. 5.9 Chemical reaction mechanism illustrating positive feedback in a linear chain of irreversible first-order reactions. The rate of production of species X1 is held constant at vf . (From [1].)

Fig. 5.10 Plots of deviation in concentration X from the stationary state value versus time for the species of the mechanism in fig. 5.9. In (a), a perturbation of the concentration of species X1 causes a pulse to propagate through the linear chain X2, X3, . . . , X8; the deviation of species X3 falls below the stationary state value, which indicates a possible feedback effect from one of the species farther in the chain. In (b), a perturbation of species X7 causes the initial slopes of the deviations in X3, X4, and X8 to be nonzero and the deviations in X3 and X4 to be mirror images about the time axis (for short times); these observations indicate that X7 activates the reaction from X3 to X4 (because the peak of X4 occurs before that of X3, implying that X3 precedes X4 in the reaction sequence) and is the precursor to X8. The maximum deviations are approximately 10% of the stationary state values or larger, except X4 in (b), which is 2% (the stationary state values of X1–X8 are 0.05, 0.0125, 0.0166, 0.1, 0.0166, 0.025, 0.01, and 0.1, respectively). (From [1].)

5.2An Example: The Glycolytic Pathway

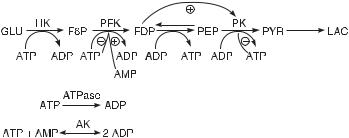
An application of the pulse method outlined above is instructive. We choose as a model a part of the glycolytic pathway shown in fig. 5.11. This model includes many of the known activations and inhibitions of enzymes by metabolites. The hexokinase reaction is assumed to be at a constant rate, which neglects the influence of ATP and glucose 6-phosphate. The concentrations of glucose, lactic acid, and the adenine nucleotide pool (the sum of the concentrations of AMP, ADP, and ATP) are taken to be constant. We represent the kinetics of this system by deterministic rate equations (see [1] for details), apply a pulse of concentration of one species to the system in a nonequilibrium stationary state, and calculate the response of the following independent species: fructose

54 DETERMINATION OF COMPLEX REACTION MECHANISMS

Fig. 5.11 Chemical reaction mechanism for an abbreviated model of the glycolytic pathway. The mechanism includes many of the known activations and inhibitions of enzymes by metabolites. Broken lines indicate activation ( ) or inhibition ( ) of enzymes by metabolites. The abbreviations for the enzymes are hexokinase (HK), phosphofructokinase (PFK), and pyruvate kinase (PK); the abbreviations for the five independent variables are fructose 6-phosphate (F6P), fructose 1,6- bisphosphate (FDP), phosphoenolpyruvate (PEP), pyruvate (PYR), and ATP (in fig. 5.12, these are labeled 1–5, respectively). (From [1].)

6-phosphate (F6P, labeled 1); fructose 1,6-bisphosphate (FDP, 2); phophoenolpyruvate (PEP, 3); pyruvate (PYR, 4); and adenosine triphophate (ATP, 5).

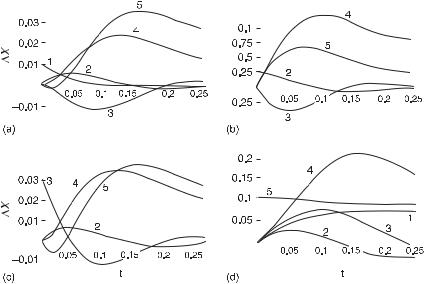
In fig. 5.12 we show the time series for the relaxation of the absolute deviation in concentration of all the five species following a pulse perturbation of one species at a time. In part (a) of that figure is plotted the response to a perturbation of species 1. Species 2, 3, and 4 have maximum response in time in succession, which tells us that species 2 follows 1, 3 follows 2, and 4 follows 3. Species 3 and 4 have zero initial slope consistent with this assignment. The deviation in 2 starts at zero, which implies that the rate of loss of 2 into any species, that is 3 and 4, is initially zero. The deviations in 3 and 4 are mirror images, which indicates that the conversion of 3 to 4 is affected by 2. If species 1 were to affect the conversion of 3 to 4, then the initial slope of 3 and 4 would be nonzero. A verification of the conversion of 1 to 4 in steps is shown in fig. 5.13; the sum of the deviations in concentrations, X1 + X2 + ( X3 + X4)/2, is nearly constant, decaying slowly in time. Thus there is an approximate conservation of mass among these species, in which each molecule of 2 produces two molecules of 3, and each molecule of 3 produces one molecule of 4. The initial slope of species 5 is equal to the negative of the initial slope of 2, from which we deduce that 5 is consumed in equal numbers to 2 produced.

The responses of all species to a pulse perturbation of species 2 are shown in fig. 5.12(b). The initial slopes of 3 and 4 are nonzero, which indicates that species 2 has a direct effect (activation) on the conversion of 3 to 4, and 2 slowly converts to 3. The minimum in 3 precedes the maximum in 4; 2 directly produces 3. If that were not the case, then the minimum in 3 would follow the maximum in 4, which is not the case. Species 1 does not respond to this perturbation, which shows that the reaction of 1 to 2 is highly irreversible. The initial slope of 5 equals that of 4, and hence 5 is produced at the same rate as 4 in the conversion of 3 to 4, which is new information.

Figure 5.12(c) shows the responses of all the species to a pulse perturbation of species 3. Both species 2 and 4 have nonzero initial slopes and from that we deduce

Fig. 5.12 Plots of time series for the absolute deviations in concentrations of species of the mechanism in fig. 5.11 with impulse perturbations of (a) F6P (1), (b) FDP (2), (c) PEP (3) and

(d) ATP (5). From an analysis of the responses to these perturbations, we deduce: 1 produces 2, 2 produces 3, 2 activates the conversion of 3 to 4, 3 produces 4, and 5 is consumed in the conversion of 1 to 2 (with the stoichiometric ratio of species 5 to species 2 being 1:1); the conversion of 1 to 2 is highly irreversible; 5 is produced at the same rate as 4 in the reaction 3 to 4; 5 is consumed at the same rate as 2 is produced, which indicates that 5 is a cosubstrate for the reverse reaction of 3 to 2; 5 inhibits the reaction of 1 to 2 and the reaction of 3 to 4. In each of the response plots, the perturbation is 10% of the stationary state value; responses are approximately several percent of the stationary state values or larger, except X5, which is in (a) and (b) (the stationary state values of X1–X5 are 0.091, 0.200, 2.70, 3.00, and 30.0, respectively). (From [1].)

that 3 produces 2 and 4. The small but present amplitude of 2 shows that the reaction 2 to 3 is reversible. Species 5 is consumed at the same rate as species 2 is produced, and thus 5 is a cosubstrate for the reaction 3 to 2. There is another transient conservation of mass in species 2, 3, and 4 (fig. 5.13b); the initial flow is from 3 to (1/2)2, and over a longer time from 3 to 4.

Finally, in fig. 5.12(d) we plot the responses of all species to a pulse perturbation of species 5. The minus signs in the figure denote reflection of deviations about the time axis. The increase in 1 and the decrease in 2 show that 5 inhibits the reaction 1 to 2, without affecting the rate of 2 to 3. The opposite rates of 3 and 4 indicate that 5 also inhibits the reaction of 3 to 4.

A summary of all the information obtained from the analysis of the results of the calculations of the responses to pulse experiments on this model is given in fig. 5.14. There is a chain from species 1 to 2 to 3 to 4. ATP is a substrate in the formation of 1 and 2; it is a product in the reaction of 2 to 3, and 3 to 4; and it is an inhibitor of the reactions of 1 to 2, and 3 to 4. The formation of 1 is irreversible, and so are the reactions

56 DETERMINATION OF COMPLEX REACTION MECHANISMS

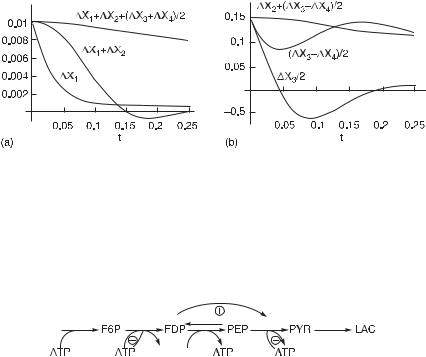
Fig. 5.13 Plots of time series for sums of deviations in concentrations for the species of the mechanism in fig. 5.11. In (a), the concentration of species X1 is perturbed; in (b), the concentration of species X3 is perturbed. Plot (a) shows that the sum of the deviations, X1 + X2 + ( X3 +X4)/2, is slowly decaying in time. From this conservation, we infer that species 2 produces two molecules of species 3, which produces species 4. Plot (b) shows a similar transient conservation of mass in species 2, 3, and 4 following a perturbation of 3; the initial flow is from 3 to (1/2)2 and over a longer time from 3 to 4. (From [1].)

Fig. 5.14 A simplified mechanism constructed from the analysis of figs. 5.12 and 5.13. This diagram captures the topology of the reaction network in fig. 5.11 and many of the effectors. (From [1].)

1 to 2, 3 to 4, and 4 to 5. The reaction 2 to 3 is reversible. Species 2 is an activator of the reaction 3 to 4.

We began with the model given in fig. 5.11, applied pulse perturbations, and from the results constructed fig. 5.14. A comparison of these two figures shows that the results of the pulse perturbations capture the topology and the causal connectivities of the reaction network and many of the effectors, both positive and negative. Further studies of adenine nucleotides are necessary to determine the roles of AMP and ADP.

Acknowledgment This chapter is based on selections from the article “Determination of causal connectivities of species in reaction networks” by William Vance, Adam Arkin, and John Ross [1], with some changes in wording.

References

[1]Vance, W.; Arkin, A.; Ross, J. Determination of causal connectivities of species in reaction networks. Proc. Natl. Acad. Sci. USA 2002, 99, 5816–5821.

[2]Tyson, J. J. Classification of instabilities in chemical reaction systems. J. Chem. Phys. 1975, 62, 1010–1015.

[3]Luo, Y.; Epstein, I. R. Feedback analysis of mechanisms for chemical oscillators. Adv. Chem. Phys. 1990, 79, 269–299.

[4]Chevalier, T.; Schreiber, I.; Ross, J. Toward a systematic determination of complex reaction mechanisms. J. Phys. Chem. 1993, 97, 6776–6787.

[5]Mihaliuk, E.; Skodt, H.; Hynne, F.; Sorenson, P. G.; Showalter, K. Normal modes for chemical reactions from time series analysis. J. Phys. Chem. 1999, 103, 8246–8251.

[6]Neiman, M. B.; Gál, D. The Kinetic Isotope Method and Its Application; Akadémic Kiadó: Budapest, 1971.