Аналитическая геометрия в пространстве.

1. Общее уравнение плоскости имеет видгденормальной вектор плоскости (рис. 6).

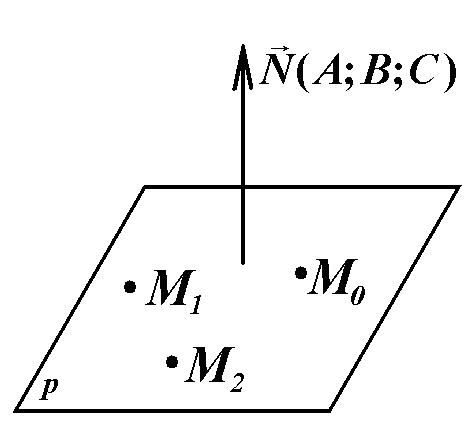
Рис.6

Уравнение плоскости, проходящей через три заданные точки иимеет вид:

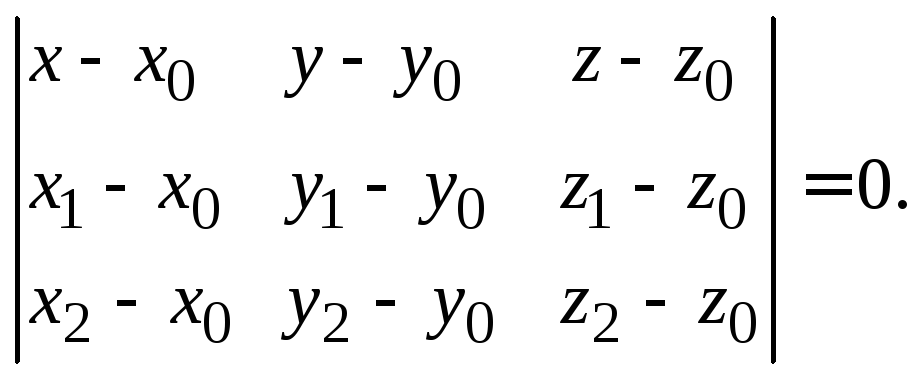(6)

2. Угол между двумя плоскостями, имеющими нормальные векторы иопределяется как угол междуикосинус этого угла находится по формуле

(7)

3. Расстояние от точки до плоскости, определяемой уравнением находится по формуле

(8)

4. Уравнение плоскости, проходящей через точку и перпендикулярной вектору , имеет вид

(9)

5. Уравнения прямой в пространстве, проходящей через две заданные точки и имеют вид:

(10)

Канонические уравнения

(11)

определяют прямую, проходящую через точку и параллельно вектору

6. Угол между двумя прямыми, заданными их каноническими уравнениями и, определяется по формуле

. (12)

7. Угол между прямой и плоскостью определяется по формуле

. (13)

Пример 3. Даны координаты вершин пирамиды Составить уравнение прямой, проходящей черези; составить уравнения плоскостейи; найти угол между реброми гранью; найти угол между плоскостямии; найти расстояние от точкидо плоскости; составить уравнение плоскости, проходящей через вершинупараллельно плоскости.

Решение. 1. Подставив координаты вершин ив формулу (10), получим уравнение прямой

().

2. Уравнение плоскости получим, подставив координаты вершинв формулу (6):

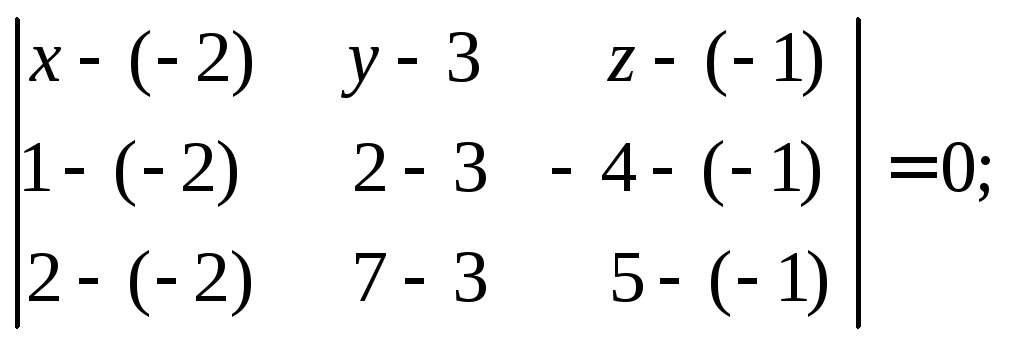
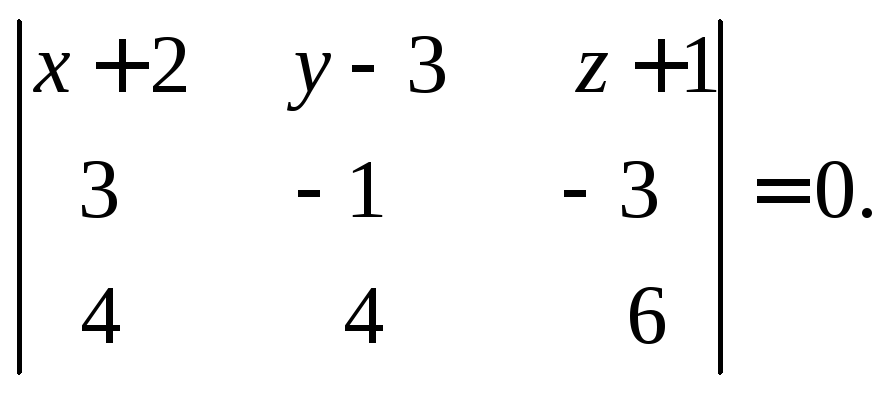
Вычислим определитель разложением по элементам 1-ой строки

(х+2)

т.е.

Аналогично получаем уравнение плоскости :.

3. Угол между ребром и граньюнайдем по формуле (13), подставив,.

0,63,

откуда =0,68 рад.

4. По уравнениям плоскостей иопределяем их нормальные векторы:,. Угол между плоскостями находим по формуле (7):

Отсюда следует, что тупой угол, равныйрад с точностью до 0,01. Это и есть искомый угол между плоскостямии.

5. Расстояние от точки () до плоскостинайдем по формуле (8):

6. Уравнение плоскости, проходящей через вершину () параллельно плоскостис нормальным вектором, получим по формуле (9):

т.е.

Тема 4. Комплексные числа.

Основные теоретические сведения.

1. Выражение вида z=x+yi= называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь мнимая единица,x=Rez действительная часть, а y=Imz–мнимая часть комплексного числа z; имодуль и аргумент числаz:

. (1)

Комплексные числа изображаются точками на комплексной плоскости (рис.7).

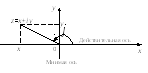
рис.7

2. Арифметические действия над комплексными числами.

Два комплексных числа иназываютсяравными, если равны их действительные и мнимые части, т.е. , если,.

Сложение (вычитание) комплексных чисел:

(2)

Умножение комплексных чисел:

(3)

В частности,

, т.е. мнимая единица есть число, квадрат которого равен .

Деление двух комплексных чисел

(4)

3. Извлечение корня n-й степени (n–натуральное число) из числа z= (z) производится по формуле

(5)

где арифметический корень из модуляz, a k=0,1, … , n1.

Пример 1. Найти полярные координаты точки М (;) (рис.8).

M

x

рис. 8

Решение. Используя формулы (1), находим полярный радиус и полярный угол точки М: ,, т.к. точкаМ лежит в IV четверти.

Пример 2. Даны комплексные числа Найти,,.

Решение.

(учли, что ).

Умножая числитель и знаменатель на сопряженное делителю комплексное число , получим

Пример 3. Изобразить на комплексной плоскости числа:1) ,

2) =2 Записать число z₁ в тригонометрической, а число z₂в алгебраической форме.

Решение. 1) Для числа z₁ имеем x₁=Re z₁=,y₁=Im z₁=0. Откладывая по оси Оx x₁=, а по осиОy =0, получаем точку комплексной плоскости, соответствующую числуz₁ (рис.9).

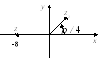
Рис.9

Модуль этого числа находим по формуле (1):. Аргумент определяем из равенства. Так как числоz₁ находится в левой полуплоскости, то его аргумент .

Тригонометрическая форма числа z₁ имеет вид z₁=8.

2) Модуль числа z₂ равен , а аргумент. Для его изображения на комплексной плоскости проводим из полюса луч под угломк полярной оси и откладываем на нем отрезок длиной=2. Полученная точка соответствует числуz₂ (рис.9). Его действительная часть а мнимая часть. Таким образом, алгебраическая форма числаz₂ имеет вид:

Пример 4. Вычислить .

Решение. Модуль числаравен 8, а аргумент равен. Используя формулу (2), получаем

При k=0:

При k=1:

.

При k=2: