8.6. Применение производной в задачах с экономическим содержанием Краткая теория

1.Функция издержекС(х) определяет затраты, необходимые для производства х единиц данного продукта. Прибыль Р(х) = D(х)–С(х), где D(х)– доход от производства х единиц продукта.

Средние издержкиА(х) при производстве х единиц продукта есть. Предельные издержки М(х) = С'(х).

2. Оптимальнымзначением выпуска для производителя является то значение х единиц продукта, при котором прибыль Р(х) оказывается наибольшей.

8.125. Функция издержек имеет вид С(x) = 100 +x², а доход при производствеxединиц товара определяется следующим образом:

Определить оптимальное для производителя значение выпуска x₀.

Решение.Функция прибыли имеет вид:

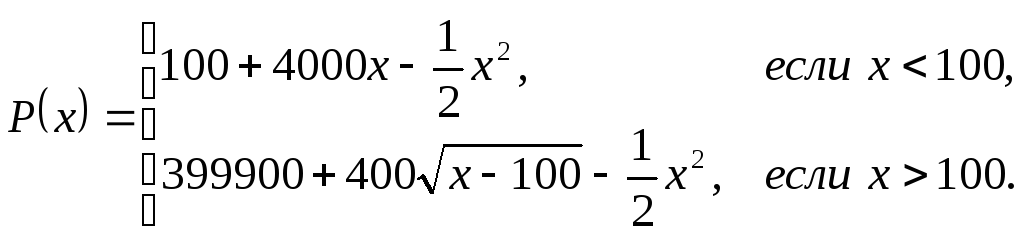
Найдем производную функции прибыли:

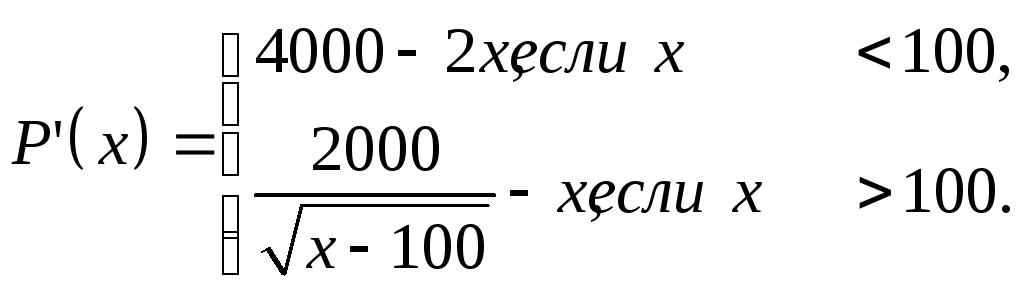
Очевидно, P'(x) > 0 приx<100, так что наибольшее значение прибыли на отрезке [0; 100] естьP(100) = 399900. Найдем теперь наибольшее значение прибыли на интервале (100; +∞). Имеется одна критическая точкаx= 200. При этомP'(x)>0 при 100<x<200 иP'(x)<0 приx>200, т.е.x= 200 – максимальное значениеP(x) на интервале (100; +∞).

P(200) = 419900 >P(100), таким образом,x_опт = 200 (ед.).

8.126. Функция издержек имеет видC(x) = 10+. На начальном этапе фирма организует производство так, чтобы минимизировать средние издержкиA(x). В дальнейшем на товар устанавливается цена, равная 4 усл. ед. за единицу. На сколько единиц товара фирме следует увеличить выпуск?

Решение.Средние издержкиA(x) =принимают минимальное значение приx= 10. Предельные издержкиM(x) =. При установившейся ценеp= 4 оптимальное значениеP(x) выпуска задается условием максимизации прибыли:

P(x) = 4x-C(x)→max, т.е. 4 =M(x), откудаx_опт = 20.

Таким образом, производство следует увеличить на 10 единиц.

8.127. Фирма минимизирует средние издержки, которые получаются в результате равными 30 руб./ед. Чему равны при этом предельные издержки?

Определить оптимальное для производителя значение выпуска x₀, при условии, что весь товар реализуется по фиксированной цене за единицуpи известен вид функции издержекC(x):

8.128. C(x) = 13 + 2x + x³; p = 14. 8.129. C(x) = 10 + x +; p = 8.

8.130.C(x) = 8 + ;p= 1,85.

Найти максимальную прибыль, которую может получить фирма производитель, при условии, что весь товар реализуется по фиксированной цене за единицу р известен вид функций издержекС(х):

8.131. р = 10,5.8.132. р =6,5.

8.133. р =40.

При производстве монополей х единиц товара цена за единицур (х).Определить оптимальное для монополии значения выпусках₀ (предполагается, что весь производственный товар реализуется), если издержкиС (х)имеют вид:

8.134. р (х) = 8-.8.135. р (х) =.

8.136. р (х) = 8-.

8.137. Монополия устанавливает фиксированную ценур = 380 за единицу товара. Издержки при производствех единиц товара равныС(х) = 292х + х² . При этом количество реализуемого товараК (х) зависит отх следующим образом:. Определить значениех, при котором монополия получит максимальную прибыль.

8.138. Монополия производит фиксированное количествох единиц товара и устанавливает на единицу товара ценур >р₀ . Количество реализуемого товараКзависит отр следующим образом (р₀– цена, при которой будет реализован весь товар):

(р₀ < 1).

Определить значение р, при котором монополия получит максимальную прибыль.

8.139. Решить задачу8.138 при условии, что

8.140. На начальном этапе производства фирма минимизирует средние издержки, причем функция издержек имеет вид. В дальнейшем цена на единицу товара устанавливается равнойр = 37.На сколько единиц товара фирме следует увеличить выпуск? На сколько при этом измениться средние издержки?

8.141. Функция издержек имеет видС(х) = 40х + 0,08х³ .Доход от реализации единицы продукции равен200. Найти оптимальное для производителя значения выпуска продукции.

8.142. Зависимость объема выпуска (в денежных единицах) продукцииV от капитальных затратх определяется функцией. Найти интервал значенийх, на котором увеличение капитальных затрат не эффективно.

8.143.Считается, что увеличение реализацииу от затрат на рекламух (млн. руб.) определяется соотношением:. Доход от реализации единицы продукции равен 20 тыс. руб. Найти уровень рекламных затрат, при котором фирма получит максимальную прибыль.

8.144. Количество реализованной монополии продукциих в зависимости от ценыр за единицу определяется соотношением. Найти значение ценыр, при котором монополия получит наибольшую прибыль.

8.145. Доход от производства продукции с использованиемх единиц ресурсов составляет величину400 .Стоимость единицы ресурсов составляет 10 усл.ед. Какое количество ресурсов следует приобрести, чтобы прибыль была наибольшей?

8.146. Функция издержек имеет видС(х) = х + 0,1х² .Доход от реализации единицы продукции равен 50. Найти максимальное значение прибыли, которое может получить производитель.

8.147. Зависимость дохода монополии от количества выпускаемой продукциих определяется какD(x) = 100x - 1000.Функция издержек на этом промежутке имеет вид:. Найти оптимальную для монополии – производителя значение выпуска продукции.

8.148. Цена на продукцию монополии – производителя устанавливается в соответствии с соотношением, идентифицируемом какр = р₀ (1-0,2).При каком значении выпуска продукции доход от ее реализации будет наибольшим?

8.149. Функция издержекС(х)имеет вид:,x > 100.В настоящий момент уровень выпуска продукциих = 200. При каком условии на параметрр фирме выгодно уменьшить выпуск продукции, если доход от реализации единицы продукции равен 50?