11.75. .

11.76. .

11.77. .

11.78. .

11.79. .

11.80..

11.81.. .

11.82. .

11.83. .

11.84. .

11.85. .

11.86. .

11.87. .

11.88. Найти площадь фигуры, заключенной между кривой и ее горизонтальной асимптотой при.

11.89. Найти объем тела, полученного при вращении вокруг оси Ох плоской фигуры, заключенной между кривой , ее вертикальной асимптотой и осьюОх на отрезке [2; 6].

11.90. Найти объем тела, полученного при вращении вокруг оси Ох фигуры, заключенной между линиями ина полуинтервале.

11.4. Приближенное вычисление определенного интеграла

Краткая теория

Пусть функция задана на отрезкеи этот отрезок разбит нап равных частей точками , , где

Тогда приближенное значение определенного интеграла от функции наможет быть найдено поформуле трапеций:

. (11.27)

Погрешность от применения формулы трапеций оценивается по формуле:

, (11.28)

где — максимальное значение модуля второй производной функциина отрезке, т.е.

.

11.91. Вычислить по формуле трапеций с точностью до 0,01.

Решение. Известно, что k-я производная функции может быть представлена в виде:, где.

Так как при любом аргументе α, то

.

Тогда и (см.(11.28))

.

Из условия находим, т.е. для достижения требуемой точности в формуле(11.27) достаточно положить n=5. Тогда . Соответственно,,,

.

Представляем теперь эти значения в (11.27), и окончательно получаем:

.

По формуле Ньютона—Лейбница , поэтому применение формулы трапеций для данного определенного интеграла позволяет, в частности, вычислить число π с требуемой точностью.

11.92. Вычислить с точностью до 0,01.

Указание: воспользоваться равенством и формулой трапеций.

11.93. Вычислить по формуле трапеций для интеграл. Найти значение погрешности полученного результата.

11.94. Вычислить по формуле трапеций для п = 8 интеграл . Найти значение погрешности полученного результата.

11.95. При каком значении п следует применить формулу трапеций для вычисления интеграла с точностью до 0,001?

11.5. Использование понятия определенного интеграла в экономике

Пусть функция описывает изменение производительности некоторого производства с течением времени. Тогда объем продукциипроизведенной за промежуток временивычисляется по следующей формуле:

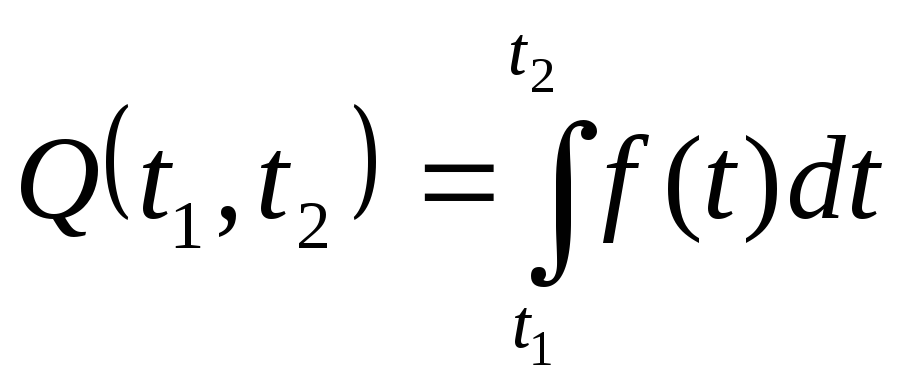(11.29)

11.96. Изменение производительности производства с течение времени от начала внедрения нового технологического процесса задается функцией , где - время в месяцах. Найти объем продукции, произведенной: а) за первый месяц; б) за третий месяц; в) за шестой месяц; г) за последний месяц года, считая от начала внедрения рассматриваемого технологического процесса.

Решение. По формуле (11.29), получаем:

.

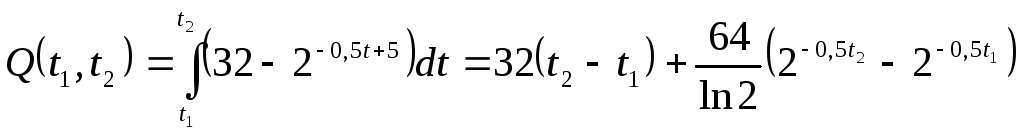Тогда: ;;

;

.

Сравнивая между собой полученные результаты, можно заметить, что основная работа по внедрению данного технологического процесса приходится, в основном, на первую половину года.

Возможность учета влияния различных факторов на изменение производительности производства связана с использованием, например, так называемых функций Кобба—Дугласа. В этом случае производительность представляется в виде произведения трех сомножителей:

,

где функции есть величины затрат природных ресурсов труда и капитала (соответственно),— некоторые числа.

11.97. Найти объем выпускаемой продукции за пять лет, если в функции Кобба—Дугласа , (t — время в годах).

Решение. Подставляя функцию производительности в формулу (11.29), получаем:

.

Применяя дважды последовательно формулу интегрирования по частям (11.13), имеем:

.

Р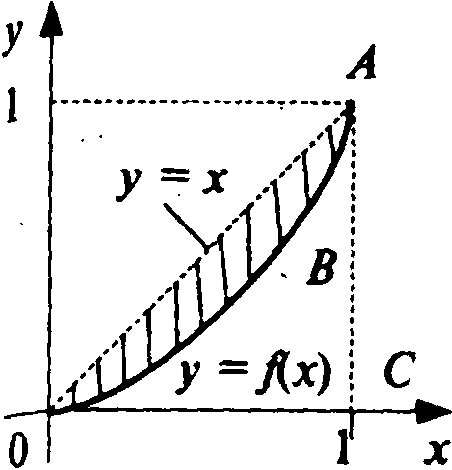ассмотрим функциюхарактеризующую неравномерность распределения доходов среди населения, гдеу — доля совокупного дохода, получаемого долей х беднейшего населения. График этой функции называется кривой Лоренца (рис. 11.17). Очевидно, что при, и неравномерность распределения доходов тем больше, чем больше площадь фигурыОАВ (см. рис. 11.17). Поэтому в качестве меры указанной неравномерности используют так

Рис. 11.17 называемый коэффициент Джини k, равный отношению площади фигуры ОАВ к площади треугольника ОА С.

11.98. По данным исследований о распределении доходов в одной из стран кривая Лоренца может быть описана уравнением , где. Вычислить коэффициент Джиниk.

Решение. По формуле (11.16) получаем

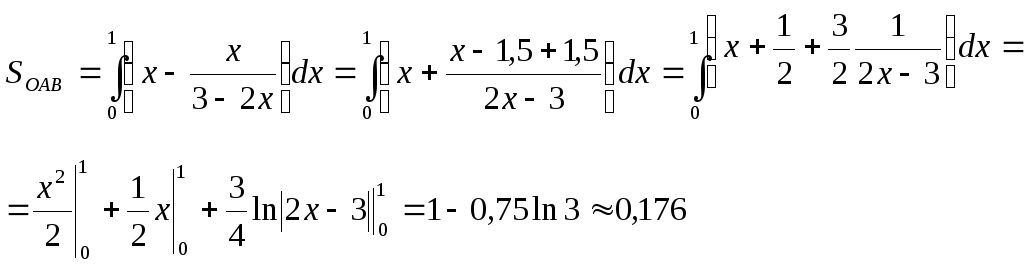
Тогда

.

П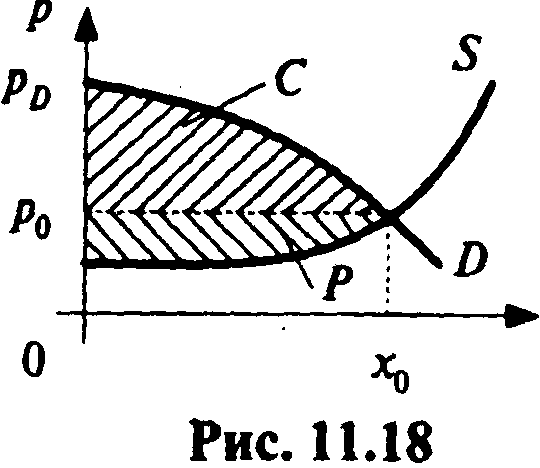усть— кривая спросаD на некоторый товар и — кривая предложения S, где p — цена на товар, х — величина спроса (предложения). Обозначим через точку рыночного равновесия (см.11.18).

Доход от реализации количества товара равновесной ценеравен произведению. Если предполагать непрерывное снижение цены от максимальной до равновеснойпо мере удовлетворения спроса, то доход составит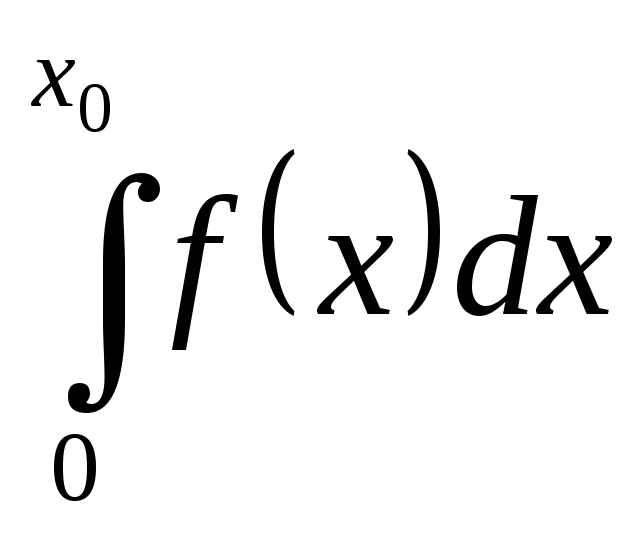. Величина денежных средств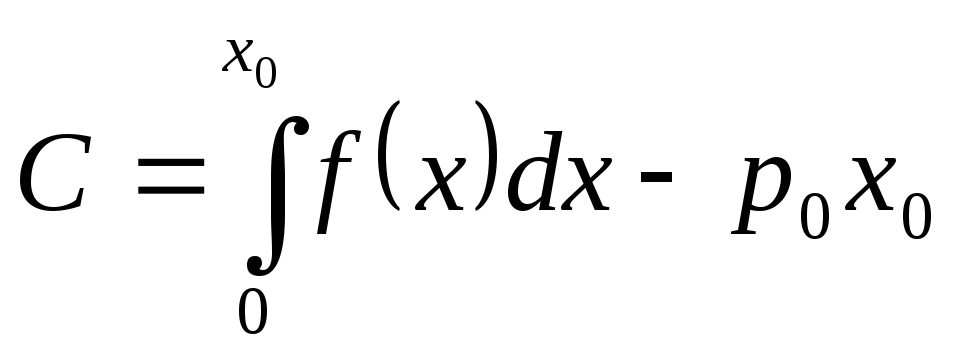сберегается потребителями, если предполагать продажу товара по равновесной ценепоэтомуС называется также выигрышем потребителей.

Аналогично, 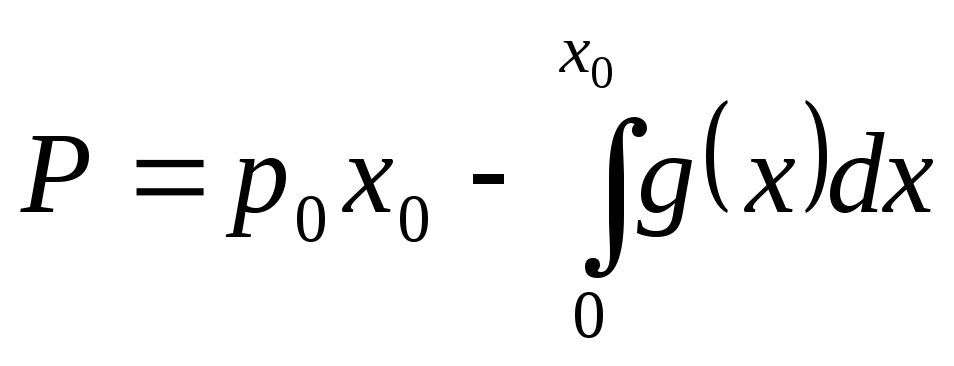называетсявыигрышем поставщиков.

Величины С и Р численно равны площадям соответствующих криволинейных треугольников (рис. 11.18).

11.99. Найти выигрыши потребителей и поставщиков в предложении установления рыночного равновесия, если законы спроса и предложения имеют вид:

.

Решение. Решая систему

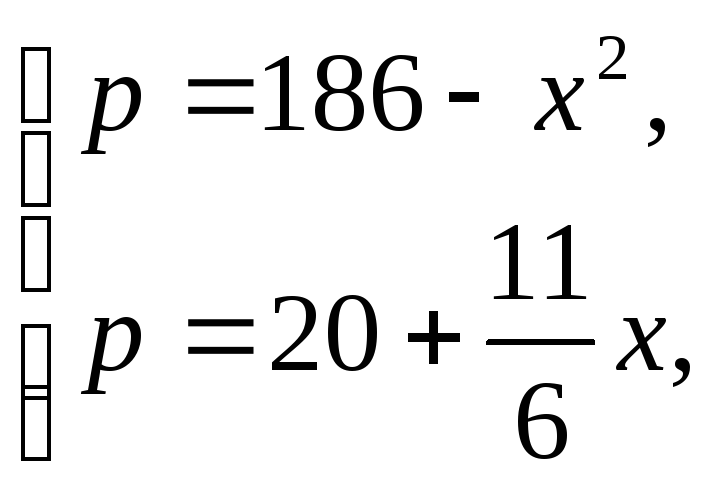
найдем точку рыночного равновесия: .

Тогда .

(ден. ед.)

11.100. Определить объем выпуска продукции за первые пять часов работы при производительности , гдеt— время в часах.

11.101. Найти объем продукции, выпущенной предприятие за год (258 рабочих дней), если ежедневная производительность этого предприятия задана функцией

, где ,t — время в часах.

11.102. При непрерывном производстве химического волокна производительность (т/ч) растет с момента запуска 10 часов, а затем остается постоянной. Сколько волокна дает аппарат в первые сутки после запуска, еслипри.

11.103. Найти объем выпуска продукции за четыре года, если в функции Кобба—Дугласа .

11.104. Кривые Лоренца распределения дохода в некоторых странах могут быть заданы уравнениями: а) ;б) ; в) .

Какую часть дохода получают 10 % наиболее низкооплачиваемого населения? Вычислить коэффициенты Джини для этих стран.

11.105. Уравнение спроса на некоторый товар имеет вид .

Найти выигрыш потребителей, если равновесная цена равна 70.

11.106. Уравнение спроса на некоторый товар имеет вид .

Найти выигрыш потребителей, если равновесное количество товара равно 10.

11.107. Найти выигрыш потребителей и поставщиков товара, законы спроса и предложения на который имеют следующий вид:

а) ,;б) ,.

76