Длина дуги кривой

5. Длинадуги кривой, заключенной между точками с абсциссами

, определяется по формуле

(11.18)

Площадь поверхности вращения

6.Площадь поверхности, образованной вращением вокруг оси кривой, заключенной между точками с абсциссами , определяется по формуле

(11.19)

Объемы тел вращения

7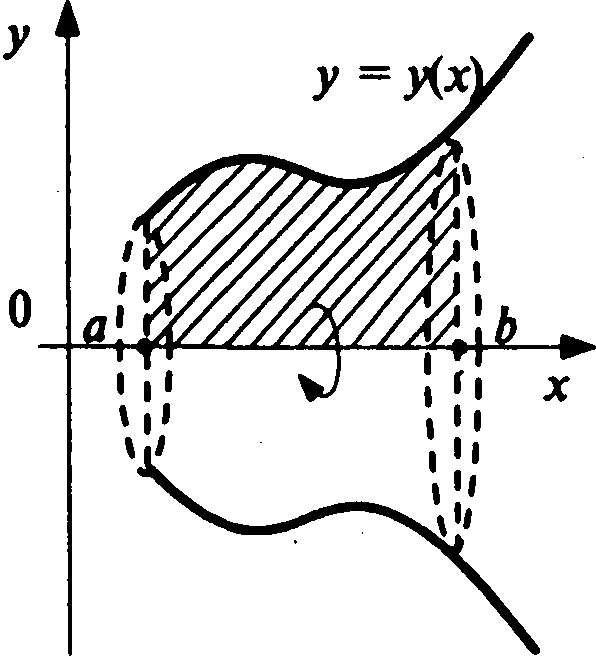.Если функциязнакопостоянна на отрезке, то объемтела, образованного вращением вокруг осиОхфигуры, ограниченной линиями(см. рис. 11.4),вычисляется по формуле

(11.20)

Рис. 11.4

А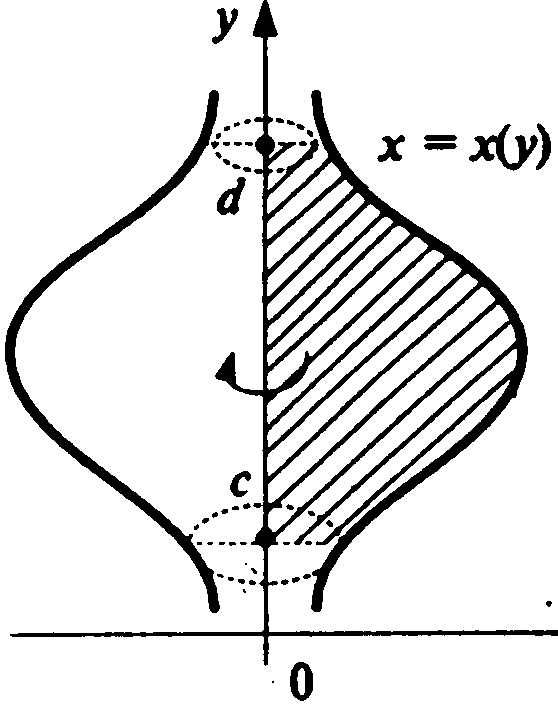налогично, объемтела, образованного при вращение вокруг осиплоской фигуры, ограниченной линиями(см.рис.11.5), вычисляется по формуле

(11.21)

Рис. 11.5

11.30. Найти площади плоских фигур, ограниченных линиями:

(фигура расположена в первой четверти);

Решение:

а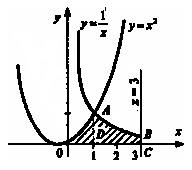)Искомая площадь- это площадь под «кривой»ОАВ (см. рис.11.6) на отрезке [0; 3].

Линия ОАВсостоит из частиОА параболыи частиАВгиперболы. Соответственно, площадь найдем как

сумму двух площадей: ,каждую из которыхРис.11.6вычислим, опираясь на геометрический смысл определенного интеграл(см. формулу (11.14)). Решая систему

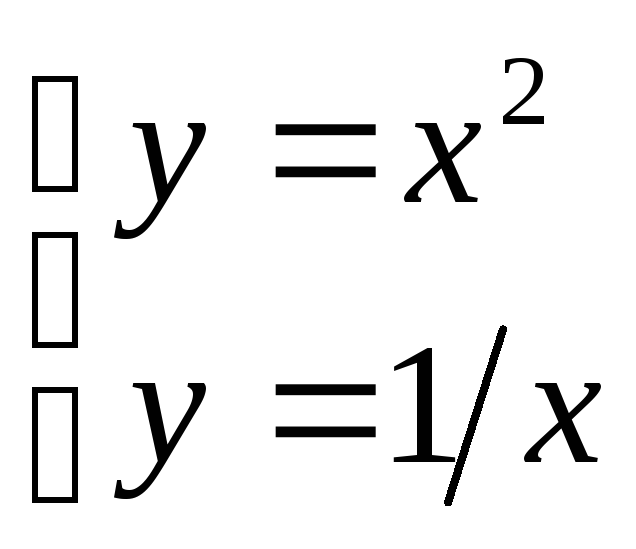
находим координаты точки А: (1, 1).

Тогда ,

и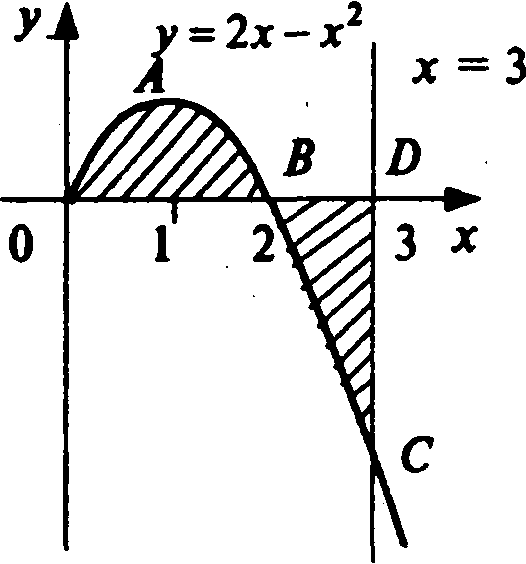(ед.² ).

б)Фигура искомой площади состоит из двух криволинейных треугольников:AOB и BCD, расположенных (соответственно) выше и ниже осиОх (см.рис.11.7). Площадь этих треугольников найдем по формулам(11.14) и (11.15):

Рис. 11.7

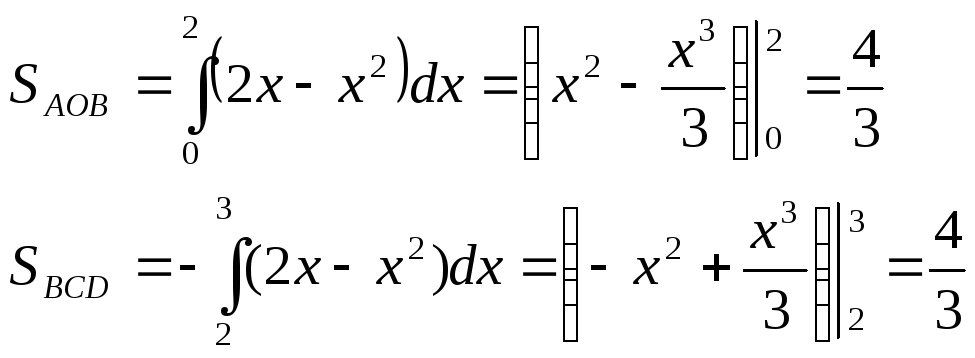
Тогда(eд.²)

11.31. Найти площадь фигуры,ограниченной осью Ох и циклоидой на отрезке[0; 2] (см. рис.11.10).

Решение. Используя формулу (11.17), получаем:

(ед.² ).

11.32. Найти длину дуги полукубической параболыот начала координат до точки с координатами (4/3,/9). Решение. Указанный участок кривой расположен в первой четверти и задается уравнением . Так как в этом случаето, применяя формулу (11.18), получаем

11.33. Найти площадь поверхности, образованной вращениемциклоиды ,при(см. рис.11.10) вокруг оси Ох.

Решение. Для получения формулы площади поверхности вращения в случае параметрического задания кривой достаточно произвести соответствующую замену переменной в исходной формуле (11.19).

Более точно, если для кривой , где, имеем,,и, то .

Полагая теперь ,, получаем выражения для искомой площади поверхности:

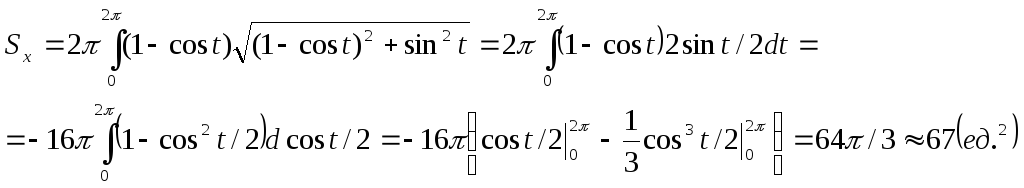
11.35.. Найти объем тела, образованного вращением вокруг оси Ох круга единичного радиуса с центром в точке (0; 2)

Решение. Отметим, что тело указанного вида в геометрии называется тором.

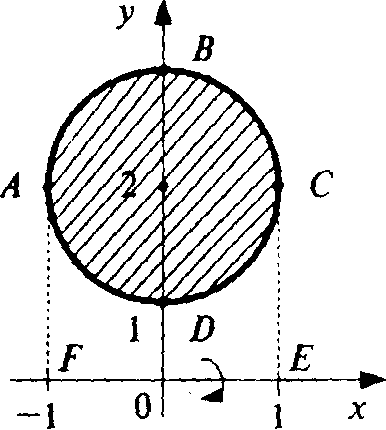Искомый объем , где— объемы, полученные при вращении вокруг оси Ох фигур, ограниченных соответственно линиями ABCEF и ADCEF (рис. 11.13). Уравнения полуокружностей ABC и ADC имеют вид:

(соответственно).

Рис. 11.13 Используя (11.20),(11.4), получаем:

.

Применяя (11.9) и результат примера 11.1, е, окончательно имеем

(ед.³)

Найти площадь фигур, ограниченных линиями:

11.36. .11.37. .