2. Свойства определенного интеграла:

1) где- некоторое число.(11.3)

2) .(11.4)

3) (11.5)

4) (11.6)

5 (11.7)

6) Теорема о среднем. Если функциянепрерывна на отрезке, то найдется такое значение,что

(11.8)

7) Если функция - четная, то

(11.9)

Если функция – нечетная, то

(11.10)

8) Формула Ньютона –Лейбница.Определенный интеграл от непрерывной на отрезкефункцииравен приращению любой ее первообразнойна этом отрезке:

,(11.11)

или

9) Замена переменной в определенном интеграле. Если функцияимеет непрерывную производную на отрезке,и функция непрерывна в каждом точке, где, то

(11.12)

10) Интегрирование по частям определенного интеграла.Если функциииимеют непрерывные производные на отрезке, то

.(11.13)

11.1. Методы вычисления определенного интеграла

11.1.Вычислить определенные интегралы:

а) ; б); в);

г) ; д); е).

Решение:

а) используя эквивалентное преобразование подынтегральной функции (почленное деление числителя на знаменатель) и свойства (11.3),(11.4) определенного интеграла, получаем

.

Все три интеграла – табличные; согласно (11.11),окончательно имеем:

.

б) Так как

то (см. (11.7))

в) Воспользуемся заменой переменной: пусть . Тогда. Найдем пределы интегрирования по переменнойt: если , то;если, то.Искомый интеграл теперь принимает вид:

.

г) Воспользуемся формулой (11.13)интегрирования по частям: пусть. Тогда,и (см.(10.13))

д) Как было отмечено выше (см. § 10.3), данный интеграл находиться с помощью последовательного применения формулы интегрирования по частям. Пусть. Тогда,и (см.(11.13)).

.

Для нахождения последнего интеграла вновь применяем формулу (11.13):,. Тогда,и

.

е) Воспользуемся тригонометрической подстановкой . Будем полагать, что. Если, то; если, то. Тогдаи

.

Так как при,. Применяя тригонометрическую формулу понижения степени, получаем:

Вычислить определенные интегралы:

11.2..11.3..11.4..11.5..

11.6.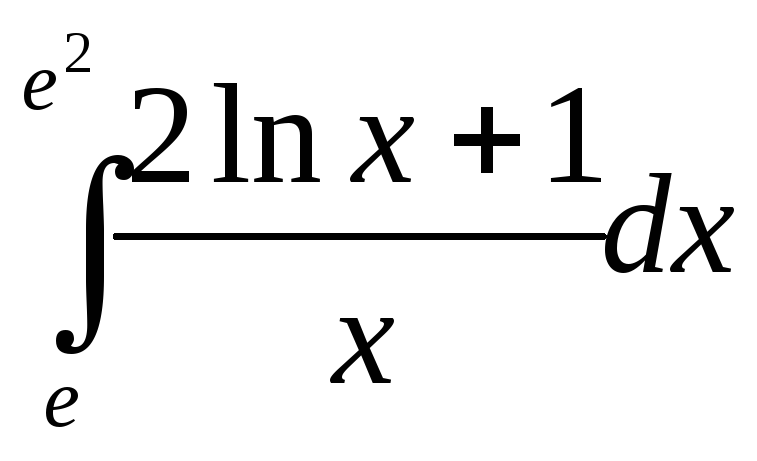.11.7..11.8..11.9..

11.10..11.11..11.12..11.13..

11.14..11.15..11.16..11.17..

11.18..11.19..11.20..11.21..

11.22..11.23..11.24..11.25..

11.26..11.27..11.28..11.29..

11.2. Геометрические приложения определенного интеграла. Краткая теория Площади плоских фигур

1.Если функциянеотрицательна на отрезке, то площадьпод кривойна( площадь криволинейной трапеции, ограниченной кривойи

прямыми ) (см.рис(11.1) численно равна определенному интегралу отна данном отрезке:

(11.14)

(геометрический смысл определенного интеграла).

Рис.11.1

2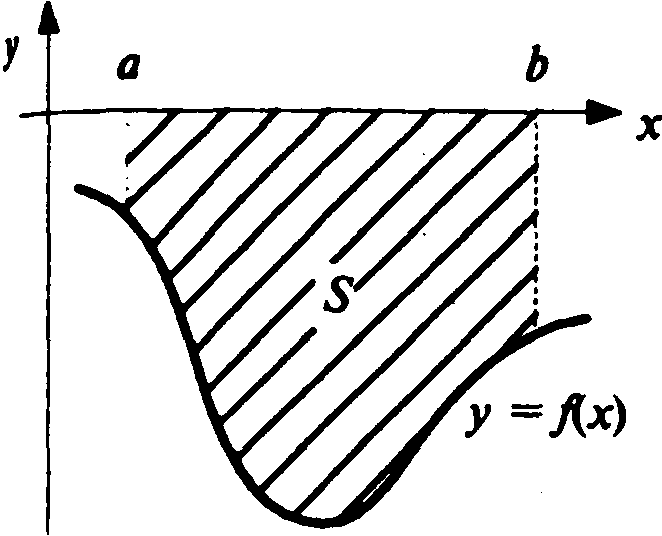. Если функция- неположительная на отрезке , то площадьнад кривойна(см.рис.11.2.) равна определенному интегралу отна, взятому со знаком «минус»:

(11.15)

Рис. 11.2

3. Если на отрезке, то площадьфигуры, заключенной между кривымиина этом отрезке определяется формулой

.(11.16)

4. Если верхняя ограничивающая линия фигуры (см. рис.11.1) задана параметрически:,, где,,, то площадьэтой фигуры вычисляется по формуле:

.(11.17)