
- •Глава 8.
- •8.1. Основные теоремы дифференциального исчисления Краткая теория
- •8.2. Правило Лопиталя Краткая теория
- •8.3. Интервалы монотонности и экстремумы функции Краткая теория
- •8.4. Интервалы выпуклости функции. Точки перегиба Краткая теория
- •8.5. Асимптоты. Исследование функций и построение их графиков Краткая теория
- •8.6. Применение производной в задачах с экономическим содержанием Краткая теория
- •Глава 9. Дифференциал функции Краткая теория
- •3.Свойства дифференциала:
- •5. Дифференциалы высших порядков.
- •9.7.9.8.
- •Глава 10. Интегральное исчисление функции одной переменной.
- •10.1.Неопределенный интеграл. Краткая теория
- •10.2. Интегрирование разложением.
- •10.3. Независимость вида интеграла от выбора аргумента функции.
- •10.4. Метод подстановки.
- •10.5. Метод интегрирования по частям.
- •10.6. Интегрирование некоторых функций, содержащий квадратный трехчлен.
- •10.7. Интегрирование рациональных функций.
- •10.138.
- •10.8. Интегрирование тригонометрических функций.
- •10.149.10.150.10.151.
- •Глава 11. Определенный интеграл Краткая теория
- •2. Свойства определенного интеграла:
- •11.1. Методы вычисления определенного интеграла
- •11.2. Геометрические приложения определенного интеграла. Краткая теория Площади плоских фигур
- •1.Если функциянеотрицательна на отрезке, то площадьпод кривойна( площадь криволинейной трапеции, ограниченной кривойи
- •Длина дуги кривой
- •Площадь поверхности вращения
- •Объемы тел вращения
- •11.38. 11.39..
- •Б. Несобственные интегралы от неограниченных функций Краткая теория
- •(11.25)
- •11.75. .
- •11.5. Использование понятия определенного интеграла в экономике
Глава 8.
8.1. Основные теоремы дифференциального исчисления Краткая теория
Теорема Ролля.Пусть функция y=ƒ(x) удовлетворяет следующим условиям:
непрерывна на отрезке [a,b];
дифференцируема на интервале (a,b);
на концах отрезка принимает равные значения, т.е. ƒ(a) = ƒ(b).
Тогда внутри отрезка существует по
крайней мере одна такая точка ξ![]() (a,b),
в которой производная равна нулю: ƒ′(ξ)
= 0.
(a,b),
в которой производная равна нулю: ƒ′(ξ)
= 0.
Теорема Лагранжа.Пусть функция y = ƒ(x) удовлетворяет следующим условиям:
непрерывна на отрезке [a,b];
дифференцируема на интервале (a,b).
Тогда внутри отрезка существует по
крайней мере одна такая точка ξ![]() (a,b),
в которой выполняется равенство:
(a,b),
в которой выполняется равенство:
ƒ′(ξ) =![]() .(8.1)
.(8.1)
8.1.Выяснить, может ли быть применена
теорема Лагранжа для функции![]() +
+![]() на отрезке:
на отрезке:
а)![]() ;б)
;б)![]() ;в)
;в)![]() .
.
Решение.
а) Функция не является непрерывной
в точкеx= 0![]()
![]() ,
поэтому на данном отрезке теорема
Лагранжа неприменима.
,
поэтому на данном отрезке теорема
Лагранжа неприменима.
б)y′ =![]() .
Производная не существует в точкеx= 1
.
Производная не существует в точкеx= 1![]()
![]() ,
поэтому на этом отрезке теорема Лагранжа
также не может быть применима.
,
поэтому на этом отрезке теорема Лагранжа
также не может быть применима.
в) на отрезке![]() оба условия теоремы Лагранжа выполнены,
так что теорема применима.
оба условия теоремы Лагранжа выполнены,
так что теорема применима.
Замечание. Если теорема Лагранжа не применима на отрезке [a,b], то это не означает, что в нем не может быть точки ξ, удовлетворяющей равенству (8.1).
8.2. Указать хотя бы одно значениеa,
при котором функцияy=![]() имеет на интервале (0;
имеет на интервале (0;![]() )
точку, в которой производная обращается
в нуль.
)
точку, в которой производная обращается
в нуль.
Решение.Очевидно, функция непрерывна
на отрезке [0;![]() ]
и дифференцируема в интервале (0;
]
и дифференцируема в интервале (0;![]() ).
Если при этом окажется, что ƒ(0) = ƒ(
).
Если при этом окажется, что ƒ(0) = ƒ(![]() ),
то требуемая точка будет существовать
по теореме Ролля. Таким образом, если
выполняется равенство
),
то требуемая точка будет существовать
по теореме Ролля. Таким образом, если
выполняется равенство
e0 +acos0
=e![]() +acos
+acos![]() ,
то условие задачи будет выполнено.
Рассматривая это равенство как уравнение
относительноa,
получаемa =
,
то условие задачи будет выполнено.
Рассматривая это равенство как уравнение
относительноa,
получаемa =
![]() -1.
-1.
Отметим, что найденное значение a, безусловно, не единственное, при котором условие задачи выполняется.
8.3. Найти все значенияa,
при которых функцияy= (1+a2)![]() удовлетворяет условиюy′
≤ 2 при всехx
удовлетворяет условиюy′
≤ 2 при всехx![]() (0;1).
(0;1).
Решение.Так как функция непрерывна
на отрезке [0;1] и дифференцируема в
интервале (0;1), то существует точка
ξ![]() (0;1)
такая, что ƒ′(ξ) = ƒ(1)-ƒ(0) =
(0;1)
такая, что ƒ′(ξ) = ƒ(1)-ƒ(0) =
= 2(1 + a2) + 2-(1 +a2) = 3+a2 ≥3, при любых значенияхa. Таким образом, ни при каких значенияха условие задачи выполняться не может.
8.4. Функцияy=![]() равна 1 приx =1 иx
=-1, ноy′ ≠ 0 для
всехx
равна 1 приx =1 иx
=-1, ноy′ ≠ 0 для
всехx![]() (-1;1).
Выяснить, противоречит ли это условиям
теоремы Ролля?
(-1;1).
Выяснить, противоречит ли это условиям
теоремы Ролля?
8.5. Выяснить, применима ли для функцииу =
![]() +
+![]() на промежутке [-2;-1]:
на промежутке [-2;-1]:
а) теорема Ролля;б) теорема Лагранжа.
8.7. Дифференцируемая при всех значенияхх функцияу = ƒ(х) удовлетворяет условиям ƒ(2) = 5, ƒ(4) = 3. Для какого значенияа уравнение ƒ′(х) =а заведомо имеет решение?
8.8. Функцияу = ƒ(х) имеет
производную, равнуюу′ = 2 +![]() +sin(2х + 3). Может ли
выполняться равенство ƒ(1)- ƒ(0) =sinα?
+sin(2х + 3). Может ли
выполняться равенство ƒ(1)- ƒ(0) =sinα?
8.2. Правило Лопиталя Краткая теория
1. Теорема( правило Лопиталя).Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных ( конечному или бесконечному), если последний существует в указанном смысле:
![]() =
=![]() .(8.2)
.(8.2)
Таким образом, правило Лопиталя
используется для раскрытия неопределенностей
вида
![]() или
или![]() .
.
2. Правило Лопиталя можно применять
также и для раскрытия неопределенностей
вида [0·∞]. Для этого произведениеf(x)g(x)
следует записать в виде![]() или
или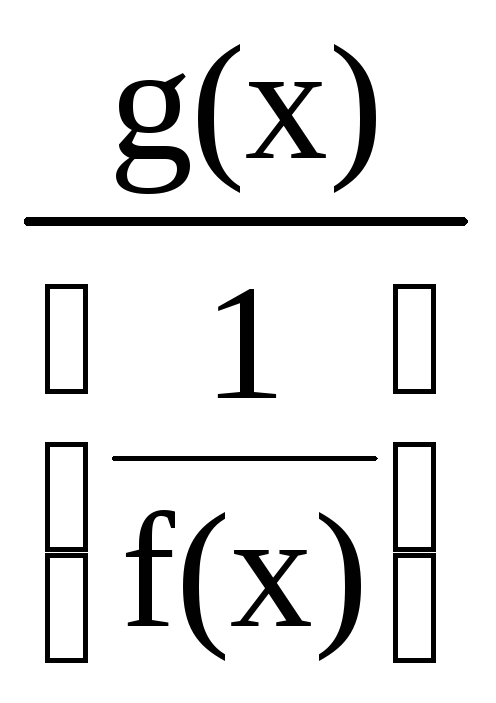 и получить неопределенность вида
и получить неопределенность вида![]() или
или![]() .
.
3.Если имеется неопределенность вида00или∞0, при вычислении предела функцииf(x)g(x), то логарифм этой функции представляет собой неопределенность вида [0·∞]. При этом используется соотношение (полученное на основе свойств логарифмов и непрерывности показательной функции):
![]() .
.
8.9. Найти![]() .
.
Решение.Так как в данном случае
имеется неопределенность вида![]() ,
можно применить правило Лопиталя(8.2):
,
можно применить правило Лопиталя(8.2):
![]() =
=![]() =
=![]()
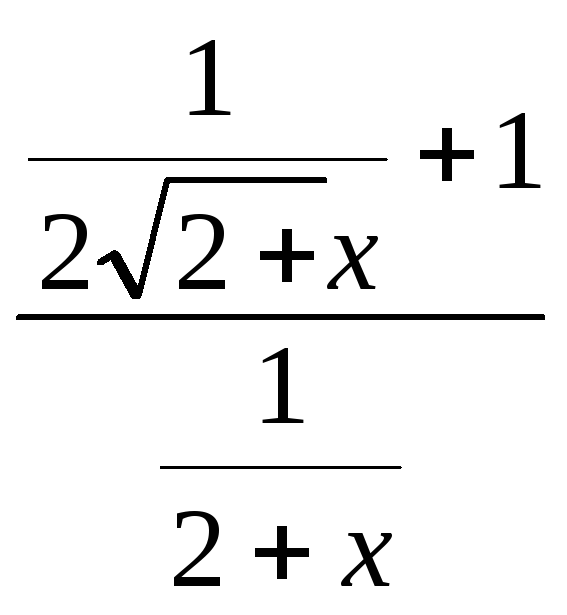 =
=![]() .
.
8.10.Найти![]()
Решение.Имеет место неопределенность
вида![]() .
Применяя правило Лопиталя(8.2),
получаем:
.
Применяя правило Лопиталя(8.2),
получаем:![]() Как видим, неопределенность вида
Как видим, неопределенность вида![]() остается. Применим правило Лопиталя
еще раз.
остается. Применим правило Лопиталя
еще раз.
![]()
Найти предел
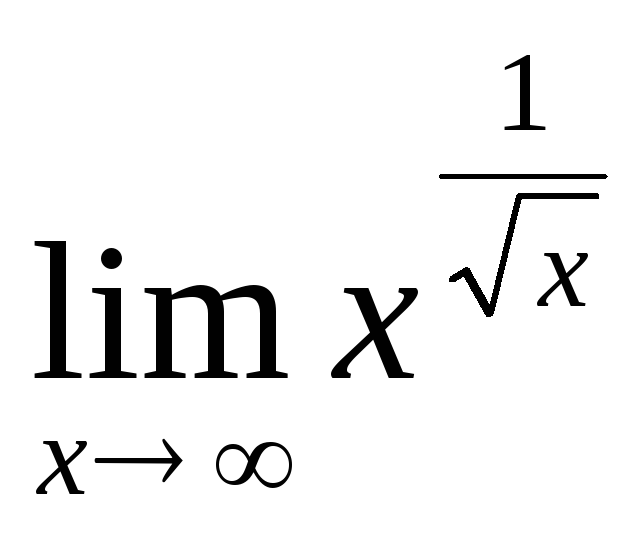 .
.
Решение.Имеем неопределенность вида∞0. найдем
 .
.
По формуле (8.3)
 .
.
8.13. Найти предел![]()
Решение.Так как при![]() ,
то
,
то![]() .
Таким образом, имеем неопределенность
вида
.
Таким образом, имеем неопределенность
вида![]() .
.
Сведем ее к неопределенности вида
![]() и применим правило Лопиталя(8.2):
и применим правило Лопиталя(8.2):

=
 .
.
8.14. Найти предел![]() .
.
Решение.Имеем неопределенность
вида![]() .
Преобразуем искомый предел
.
Преобразуем искомый предел![]() и найдем отдельно предел
и найдем отдельно предел![]() ,
используя правило Лопиталя(8.2):
,
используя правило Лопиталя(8.2):
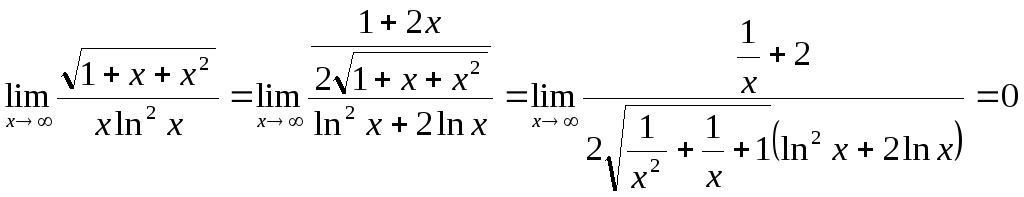 .
.
Таким образом,
![]() .
.
Найти пределы, используя правило Лопиталя:
8.15.![]() .8.16.
.8.16.![]() .8.17.
.8.17.![]() .
.
8.18.![]() .8.19.
.8.19.![]() .8.20.
.8.20.![]()
8.21.![]() .8.22.
.8.22.![]() .8.23.
.8.23. .
.
8.24.![]() .8.25.
.8.25. .8.26.
.8.26.![]() .
.
8.27.![]() .8.28.
.8.28.![]() .8.29.
.8.29.![]() .
.
8.30.![]() .8.31.
.8.31.![]()
![]() .8.32.
.8.32.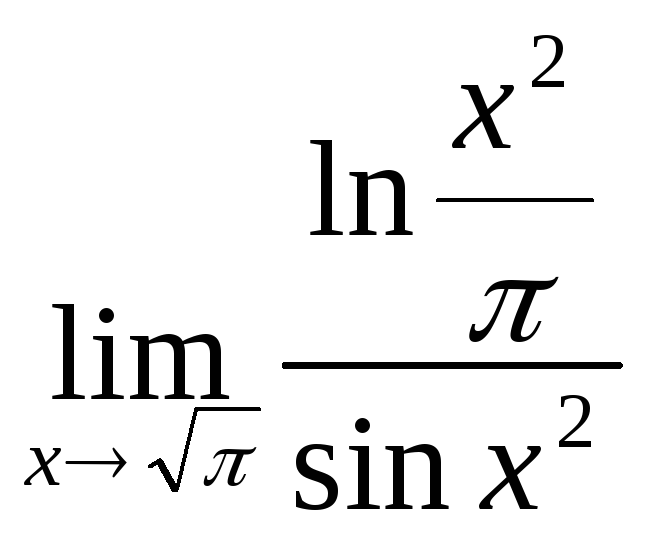 .
.
8.33.![]() .8.34.
.8.34.![]() .
.
