Практикум по механике и молекулярной физике

площади соприкасающихся слоев жидкости при градиенте скорости между ними, равном единице.

Как следует из формулы (1), в системе СИ коэффициент вязкости η

измеряется в Н·с/м2=Па·с (паскаль-секунда), а в системе СГС в дн·с/см2=г/см·с (Пуаз).

Рассмотрим падение твердого тела в форме шарика в вязкой жидкости (рис. 2). На шарик действуют три силы: сила тяжести f1 = mg, подъемная, или выталкивающая сила (закон Архимеда), – f2 и сила сопротивления движению шарика, обусловленная силами внутреннего трения жидкости, – f3. При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. Ближайшие смежные слои жидкости также приводятся в движении, но получаемая ими скорость тем меньше, чем дальше они находятся от шарика. Таким образом, при вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.

Сила сопротивления движению шарика определяется формулой Сто-

где v – скорость движения шарика, r – его радиус.

С учетом действия на шарик трех сил уравнение движения в общем

где ρ – плотность шарика, ρ1 – плотность вязкой жидкости, g – ускорение свободного падения.

Все три силы, входящие в правую часть уравнения (3), будут направлены по вертикали: сила тяжести – вниз, подъемная сила и сила сопротивления – вверх.

Сила сопротивления с увеличением скорости движения шарика возрастает. При некоторой скорости шарика сила сопротивления становится

равной сумме сил тяжести, т. е. f3 = f2 + f1. Таким образом, равнодейст-

71

вующая этих сил обращается в нуль. Это означает, что уравнение (3) при-

Таким образом, по достижении шариком скорости v0 далее он движется с постоянной скоростью и уравнение (3) принимает следующий вид:

длина пути, проходимого шариком при установившемся движении, t – время его движения, а также плотности ρ и ρ1 и размеры шарика, можно вычислить значение коэффициента вязкости для данной жидкости по фор-

муле η = 2 (ρ − ρ1 )gd 2t. (6)

9 4A

Выполнение работы Задание 1. Определение диаметров шариков

Измерение диаметров шариков производится с помощью микроскопа. Для измерения диаметра шарика необходимо поступить следующим образом. Положив шарик внутрь шайбы на предметном столике микроскопа, включить осветитель. Регулировкой положения осветителя и зеркальца осветить шарик снизу. При правильной регулировке осветителя и зеркальца наблюдаемое в окуляр поле зрения должно быть наиболее ярким. Вращая окуляр, добиться резкого изображения перекрестия нитей. Установить тубус на такую высоту, чтобы отчетливо были видны края шарика (при правильной регулировке осветителя и зеркальца в поле зрения должно быть видно изображение шарика в виде черного круглого пятна на фоне яркого поля зрения). Перемещая при помощи микрометрического винта тубус микроскопа, навести вертикальную нить окуляра последовательно на края

шарика, чтобы нить казалась касательной шарику

(рис. 3). В положениях 1 Положение 1 Рис. 3 Положение 2 и 2 снимаются отсчеты а1

и а2 по шкале в миллиметрах, а по барабану – отсчеты, выраженные в сотых долях миллиметра (один полный оборот барабана равен горизонтальному перемещению тубуса на один миллиметр). Разность между двумя отсчетами (а1 и а2) дает

72

диаметр шарика d. Шарики имеют не совсем правильную форму, поэтому необходимо диаметр каждого шарика измерять не менее трех раз, поворачивая после каждого измерения шарик на предметном столике микроскопа с помощью пинцета. Шарики с ярко выраженными поверхностными дефектами использовать для опыта не рекомендуется.

Количество шариков, необходимое для выполнения работы, указывается преподавателем.

Задание 2. Определение коэффициента вязкости исследуемой жидкости

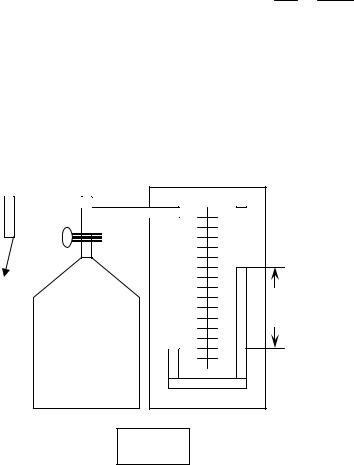
Прибор для определения коэффициента вязкости жидкости состоит из стеклянного цилиндра, наполненного исследуемой жидкостью и имеющего горизонтальные, подвижные металлические обручи 1 и 2 (рис.4). Рас-

стояние между обручами A задается преподавателем.

Для измерения коэффициента внутреннего трения в данной работе используются маленькие шарики из свинца. Измерив предварительно диаметры шариков, опускают их в цилиндр с вязкой жидко-

Астью (касторовое масло) через отверстие А в крышке ци-

линдра. Скорости шариков довольно значительны, поэтому

1глаз наблюдателя необходимо установить против верхнего обруча 1 так, чтобы обруч сливался в одну полосу. Считая

Aдвижение установившимся к моменту прохождения шариком верхнего обруча, в момент прохождения шарика через

Рис. 4

ляется время t движения шарика между обручами 1 и 2. Расстояние A между обручами измеряется масштабной линейкой.

Подставляя в формулу (6) значения A , t и среднее значение диаметра шарика, вычисляют значение коэффициента вязкости η исследуемой жидкости.

В нашем случае ρ = 11,30 г/см3, ρ1 = 0,96 г/см3. Так как внутреннее трение жидкостей сильно зависит от температуры, то необходимо отметить температуру во время проведения опыта.

Проведя эксперимент с указанным числом шариков, вычисляют значения коэффициентов вязкости η для каждого шарика, а затем вычисляют среднюю абсолютную и относительную ошибки измерений. Полученные результаты заносятся в таблицу.

73

Контрольные вопросы

1.1.Объясните механизм внутреннего трения в жидкостях.

2.Объясните физический смысл коэффициента вязкости.

3.В каких единицах измеряется коэффициент вязкости в ед. СИ и системе СГС?

4.Выведите рабочую формулу (6), поясните этот вывод.

5.Как зависит коэффициент вязкости от температуры?

6.Что представляет собой градиент скорости? Дайте определение этой величины.

РАБОТА № 12 ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ

ГАЗОВ МЕТОДОМ КЛЕМАНА – ДЕЗОРМА

Приборы и принадлежности: стеклянный баллон с трехходовым краном, манометр, воздушный насос.

Краткая теория

Опыт показывает, что количество теплотыQ , необходимое для на-

гревания массы однородного вещества от температуры Т1 до Т2 градусов, пропорционально массе вещества и изменению температуры:

Отсюда видно, что удельной теплоемкостью называется количество теплоты, необходимое для нагревания вещества массой 1 кг на 1 К.

Кроме удельной теплоемкости вещества вводится понятие молярной теплоемкости С. Молярной теплоемкостью называется количество теплоты, необходимое для нагревания моля вещества на 1 К. Из определения удельной теплоемкости следует, что она связана с молярной соотношением

где μ– молярная масса вещества. Единицей С является Дж/(моль К). Состояние газа может быть охарактеризовано тремя величинами –

параметрами состояния: давлением p, объемом V и температурой T. Уравнение, связывающее эти величины, называется уравнением состояния вещества. Для случая идеального газа уравнением состояния является уравнение Менделеева – Клапейрона, которое для одного моля газа будет иметь вид pV = RT (4)

74

где R – универсальная газовая постоянная.

Величина теплоемкости газов зависит от условий нагревания. Выясним эту зависимость, воспользовавшись уравнением состояния (4) и первым началом термодинамики, которое можно сформулировать следующим образом:

количество теплоты dQ , переданное системе, затрачивается на увеличе-

Из уравнения (6) видно, что теплоемкость может иметь различные значения в зависимости от способов нагревания газа, так как одному и тому же значению dΤ могут соответствовать различные значения dU и dΑ. Элементарная работа dΑ равна dΑ = pdV.

где i – число степеней свободы.

Числом степеней свободы газа называется число независимых координат, определяющих положение тела в пространстве.

При движении точки по прямой линии для оценки ее положения надо знать одну координату, т. е. точка имеет одну степень свободы. Если точка движется по плоскости, ее положение характеризуется двумя координатами, т. е. точка обладает двумя степенями свободы. Положение материальной точки в пространстве определяется тремя координатами.

Число степеней свободы молекулы обычно обозначается буквой i-. Молекулы, которые состоят из одного атома, считаются материальными точками и имеют число степеней свободы i- = 3. Такими являются молеку-

но пренебречь, т. к. момент инерции ее относительно этой оси очень мал. Молекулы, состоящие из трех и более жестко связанных атомов, не лежащих на одной прямой (рис. 1б), имеют число степеней свободы i = 6: три степени свободы поступательного движения и три степени свободы вращения вокруг осей X, Y, Z. Столько же степеней свободы имеют и другие многоатомные молекулы.

Рассмотрим основные процессы, протекающие в идеальном газе при изменении температуры, когда масса газа остается неизменной и равна од-

75

ному молю. Количество теплоты, необходимое для нагревания одного моля газа на 1 К, определяется молярной теплоемкостью.

Изохорический процесс. Процесс называется изохорическим, если объем тела при изменении температуры остается постоянным, т. е. V = const. В этом случае dV = 0 . Следовательно, и dA = 0, т. е. при этом вся подводимая к газу теплота идет на увеличение его внутренней энергии. Тогда из уравнения (6) следует, что молярная теплоемкость газа при по-

Изобарический процесс. Процесс, протекающий при постоянном давлении (P = const), называется изобарическим. Для этого случая форму-

Изотермический процесс. Изотермическим процессом называется процесс, протекающий при постоянной температуре (T = const). В этом случае dT = 0 и dQ = dA, т. е. внутренняя энергия газа остается постоян-

ной и все подводимое тепло расходуется на работу.

Адиабатический процесс. Процесс, протекающий без теплообмена с окружающей средой, называется адиабатическим. Первое начало термодинамики для такого процесса будет иметь вид (dQ = 0, dU + dA = 0 ):

dA = −dU = −cV dT ,

т.е. при адиабатическом процессе расширения или сжатия работа совершается газом только за счет изменения запаса внутренней энергии.

Выведем уравнение адиабатического процесса. При адиабатическом расширении работа совершается за счет убыли внутренней энергии

dA = −dU.

где γ =cp . называется отношением удельных теплоемкостей cV

Интегрируя и потенцируя, получим уравнение Пуассона:

76

77

Если сразу после открывания снова закрыть кран, то давление внутри баллона начнет возрастать вследствие того, что охладившийся при расширении воздух в баллоне станет снова нагреваться. Возрастание давления прекратится, когда температура воздуха в баллоне сравняется с внешней температурой Т1. Обозначим давление воздуха в баллоне в этот момент через р2 и соответствующее показание манометра – через h2. Это будет третье состояние газа: Т1 и р2. Ясно, что p2 = p0 + h2 . (16)

Так как переход от второго состояния (после закрытия крана) к третьему произошел без изменения объема, то можно применить здесь закон Гей-

Эта форма уравнения Пуассона может быть легко получена из обычной (13) p1V1γ = p2V2γ , если воспользоваться для этой цели уравнением состоя-

Разлагая оба двучлена по биному Ньютона и ограничиваясь членами первого порядка малости, получаем:

Но выражение, стоящее в левой части этого уравнения, есть не что иное, как h2; действительно, подставив в уравнение (17) значение р1 из уравне-

ния (16) и разрешив его относительно h2, получим: h2 = p0 T1 −T2 .

T2

Следовательно, можно записать: h2 = γ γ−1 h1 , откуда окончательно нахо-

78

Выполнение работы

С помощью трехходового крана Д баллон может соединяться с воздушным насосом, с атмосферой либо перекрываться совсем.

Для проведения измерений кран ставят в положение, при котором воздух нагнетается в баллон с помощью насоса. Когда разность уровней в манометре достигает 20–25 делений шкалы манометра, отключают баллон от насоса и атмосферы. После того как давление окончательно установится, производят отсчет h1 – разности уровней жидкости в обоих коленах манометра (если нуль шкалы манометра находится внизу, то h1 определяется как разность уровней в манометре; если нуль шкалы находится в середине, то берется сумма показаний манометра по обе стороны от нуля). Затем производят на некоторый момент сообщение баллона с атмосферой и быстро его перекрывают (рекомендуется перекрывать баллон сразу после прекращения звука выходящего воздуха). Когда давление окончательно

установится, производят второй отсчет по манометру – h2.

Опыт повторить не менее десяти раз, меняя всякий раз величину h1. Подставляя в формулу (19) значения h1 и h2, взятые из отдельных на-

блюдений, находят величину , а все результаты заносят в таблицу:

1

...

10

Ср.

Окончательно величину находят как среднее значение всех , полученных при наблюдении.

Контрольные вопросы

1.Что называется удельной (молярной) теплоемкостью вещества?

2.Почему теплоемкости газа зависят от условий его нагревания?

3.Что называется числом степеней свободы тела?

4.Чему равно отношение молярной теплоемкости газа и его удельной теплоемкости?

5.Чему равно для воздуха?

6.Дайте определение адиабатического процесса и покажите, как в

координатах P и V графически изображаются адиабатический и изотермический процессы.

79

РАБОТА № 13

ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ И ОТНОШЕНИЕ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ СР/СV ДЛЯ ВОЗДУХА МЕТОДОМ СТОЯЧИХ ЗВУКОВЫХ ВОЛН

Особым примером результата интерференции двух волн служат так называемые стоячие волны, образующиеся в результате наложения двух встречных когерентных волн с одинаковыми амплитудами.

Предположим, что две плоские волны с одинаковыми амплитудами, отстоящие на полпериода, распространяются – одна вдоль положительного

направления Y, другая – вдоль отрицательного направления Y (рис. 1). Ес-

ли начало координат в такой точке, в которой встречные волны имеют одинаковые фазы, и выбрать отсчет времени так, чтобы начальные фазы оказались равными нулю, то уравнения обеих бегущих волн будут иметь

Разные знаки в аргументах синусов обусловлены тем, что волны движутся

навстречу друг другу, т. е. их скорости V различаются по знаку.

По принципу суперпозиции (наложения) интерферирующих волн

смещение X в результирующей волне будет равно:

80